Quant Practice Questions for ACT - 1 | Mathematics for ACT PDF Download
Q1: A ladder leans against a wall forming a 60∘ angle between the ground and the ladder. If the bottom of the ladder is 30 feet away from the wall, how long is the ladder?
(a) 30 feet
(b) 40 feet
(c) 50 feet
(d) 60 feet
 View Answer
View AnswerAns: (d)
The relationship among all sides of special right triangle 30∘ -60∘ - 90∘ is provided in this triangle: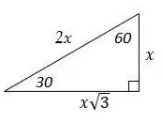 In this triangle, the opposite side of 30∘ angle is half of the hypotenuse. Draw the shape of this question: The latter is the hypotenuse. Therefore, the latter is 60 ft.
In this triangle, the opposite side of 30∘ angle is half of the hypotenuse. Draw the shape of this question: The latter is the hypotenuse. Therefore, the latter is 60 ft.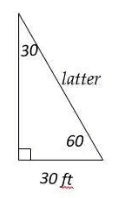
Q2: When 40% of 60 is added to 12% of 600, the resulting number is:
(a) 24
(b) 72
(c) 96
(d) 140
 View Answer
View AnswerAns: (c)
40% of 60 equals to: 0.40 × 60 = 24
12% of 600 equals to: 0.12 × 600 = 72
40% of 60 is added to 12% of 600: 24 + 72 = 96
Q3: How long does a 420–miles trip take moving at 50 miles per hour (mph)?
(a) 4 hours
(b) 6 hours and 24 minutes
(c) 8 hours and 24 minutes
(d) 8 hours and 30 minutes
 View Answer
View AnswerAns: (c)
Use distance formula:
𝐷𝑖𝑠𝑡𝑎𝑛𝑐𝑒 = 𝑅𝑎𝑡𝑒 × 𝑡𝑖𝑚𝑒 ⇒ 420=50×𝑇, divide both sides by 50. 420/50 = 𝑇 ⇒ 𝑇 = 8.4 hours.
Change hours to minutes for the decimal part. 0.4 hours = 0.4 × 60 = 24 minutes.
Q4: Right triangle ABC is shown below. Which of the following is true for all possible values of angles A and B?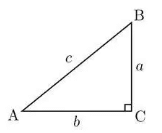 (a) tan A = tan B
(a) tan A = tan B
(b) sin A = cos B
(c) tan2 A = tan2
(d) tan A = 1
 View Answer
View AnswerAns: (b)
By definition, the sine of an acute angle is equal to the cosine of its complement.
Since angle A and B are complementary angles, therefore:
sin A = cos B
Q5: What is the area of a square whose diagonal is 8 cm?
(a) 16 𝑐𝑚2
(b) 32 𝑐𝑚2
(c) 34 𝑐𝑚2
(d) 128 𝑐𝑚2
 View Answer
View AnswerAns: (b)
The diagonal of the square is 8. Let 𝑥 be the side.
Use Pythagorean Theorem: 𝑎2+𝑏2 = 𝑐2
𝑥2 + 𝑥2 = 82 ⇒ 2𝑥2 = 82 ⇒ 2𝑥2 = 64 ⇒ 𝑥2 = 32 ⇒ 𝑥 = √32
The area of the square is:
√32 × √32 = 32
Q6: What is the value of 𝑥 in the following figure?
(a) 150
(b) 145
(c) 125
(d) 105
 View Answer
View AnswerAns: (b)
𝑥 = 20 + 125 = 145
Q7: What is the value of y in the following system of equation?
3𝑥−4𝑦=−20
−𝑥+2𝑦=10
(a) −1
(b) −2
(c) 1
(d) 5
 View Answer
View AnswerAns: (d) Solve the system of equations by elimination method.
3𝑥−4𝑦 = −20
−𝑥+2𝑦 = 10
Multiply the second equation by 3, then add it to the first equation.
3𝑥−4𝑦 = −20
3(−𝑥+2𝑦 = 10)
⇓
3𝑥 − 4𝑦 = −20
−3𝑥 + 6𝑦 = 30)
⇒ add the equations
2𝑦 = 10 ⇒ 𝑦 = 5
|
144 videos|100 docs|61 tests
|
FAQs on Quant Practice Questions for ACT - 1 - Mathematics for ACT
| 1. What are some tips for effectively preparing for the ACT exam? |  |
| 2. How can I improve my time management during the ACT exam? |  |
| 3. What should I bring with me on the day of the ACT exam? |  |
| 4. Are there any specific strategies for tackling the Math section of the ACT exam? |  |
| 5. How can I stay calm and focused during the ACT exam? |  |

|
Explore Courses for ACT exam
|

|
















