Increasing and Decreasing Functions | Mathematics for NDA PDF Download
Applications of Derivatives in Maths
The derivative is defined as the rate of change of one quantity with respect to another. In terms of functions, the rate of change of function is defined as dy/dx = f(x) = y’.
The concept of derivatives has been used in small scale and large scale. The concept of derivatives used in many ways such as change of temperature or rate of change of shapes and sizes of an object depending on the conditions etc.,
Rate of Change of a Quantity
This is the general and most important application of derivative. For example, to check the rate of change of the volume of a cube with respect to its decreasing sides, we can use the derivative form as dy/dx. Where dy represents the rate of change of volume of cube and dx represents the change of sides of the cube.
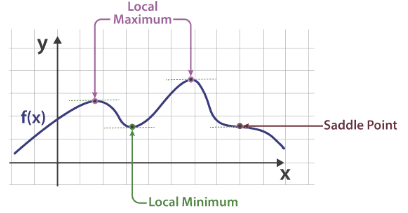
Increasing and Decreasing Functions
To find that a given function is increasing or decreasing or constant, say in a graph, we use derivatives. If f is a function which is continuous in [p, q] and differentiable in the open interval (p, q), then,
- f is increasing at [p, q] if f'(x) > 0 for each x ∈ (p, q)
- f is decreasing at [p, q] if f'(x) < 0 for each x ∈ (p, q)
- f is constant function in [p, q], if f'(x)=0 for each x ∈ (p, q)
Tangent and Normal To a Curve
A tangent is a line that touches the curve at a point and doesn’t cross it, whereas normal is perpendicular to that tangent.
Let the tangent meet the curve at P(x1, y1).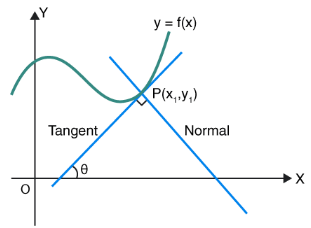
Now the straight-line equation which passes through a point having slope m could be written as;y – y1 = m(x – x1)
We can see from the above equation, the slope of the tangent to the curve y = f(x) and at the point P(x1, y1), it is given as dy/dx at P(x1, y1) = f'(x). Therefore,
Equation of the tangent to the curve at P(x1, y1) can be written as:
y – y1 = f'(x1)(x – x1)
Equation of normal to the curve is given by;
y – y1 = [-1/ f'(x1)] (x – x1)
Or
(y – y1) f'(x1) + (x-x1) = 0
Maxima and Minima
To calculate the highest and lowest point of the curve in a graph or to know its turning point, the derivative function is used.
- When x = a, if f(x) ≤ f(a) for every x in the domain, then f(x) has an Absolute Maximum value and the point a is the point of the maximum value of f.
- When x = a, if f(x) ≤ f(a) for every x in some open interval (p, q) then f(x) has a Relative Maximum value.
- When x= a, if f(x) ≥ f(a) for every x in the domain then f(x) has an Absolute Minimum value and the point a is the point of the minimum value of f.
- When x = a, if f(x) ≥ f(a) for every x in some open interval (p, q) then f(x) has a Relative Minimum value.
Monotonicity
Functions are said to be monotonic if they are either increasing or decreasing in their entire domain. f(x) = ex, f(x) = nx, f(x) = 2x + 3 are some examples.
Functions which are increasing and decreasing in their domain are said to be non-monotonic
For example: f(x) = sin x , f(x) = x2
Monotonicity Of A function At A Point
A function is said to be monotonically decreasing at x = a if f(x) satisfy;
f(x + h) < f(a) for a small positive h
- f'(x) will be positive if the function is increasing
- f'(x) will be negative if the function is decreasing
- f'(x) will be zero when the function is at its maxima or minima
Approximation or Finding Approximate Value
To find a very small change or variation of a quantity, we can use derivatives to give the approximate value of it. The approximate value is represented by delta △.
Suppose change in the value of x, dx = x then,
dy/dx = △x = x.
Since the change in x, dx ≈ x therefore, dy ≈ y.
Point of Inflection
For continuous function f(x), if f'(x0) = 0 or f’”(x0) does not exist at points where f'(x0) exists and if f”(x) changes sign when passing through x = x0 then x0 is called the point of inflection.
(a) If f”(x) < 0, x ∈ (a, b) then the curve y = f(x) in concave downward
(b) if f” (x) > 0, x ∈ (a, b) then the curve y = f(x) is concave upwards in (a, b)
For example: f(x) = sin x
Solution: f'(x) = cos x
f”(x) = sinx = 0 x = nπ, n ∈ z
Application of Derivatives in Real Life
- To calculate the profit and loss in business using graphs.
- To check the temperature variation.
- To determine the speed or distance covered such as miles per hour, kilometre per hour etc.
- Derivatives are used to derive many equations in Physics.
- In the study of Seismology like to find the range of magnitudes of the earthquake.
Applications of Derivatives Examples
Example 1: Show that the function f(x) = x3 – 2x2 + 2x, x ∈ Q is increasing on Q.
Sol:
f(x) = x3 – 2x2 + 2x
By differentiating both sides, we get,
f'(x) = 3x2 – 4x + 2 > 0 for every value of x
Therefore, f is increasing on Q.
Example 2: The tangent to the curve y=x2 − 5x + 5 parallel to the line 2y = 4x + 1, also passes through a point. Find the coordinates of the point.
Sol:
dy/dx = 2x – 5|x=x1 = 2
2x1 = 7
⇒x1 = 7/2
y1 = (49/4) – (35/2) + 5 = (49 – 70 + 20)/4 = -¼
y + ¼ = 2(x – 7/2)
4y + 1 = 8x – 28
⇒ 8x – 4y – 29 = 0
x = ⅛, y = -7 satisfies the equation
|
284 videos|295 docs|232 tests
|