How to draw direct and inverse proportion graphs - Year 7 PDF Download
Key points
 Image caption
Image captionParaphrase the information given
- Summarize and simplify complex content from PDF books into concise, understandable notes.
- Extract key theoretical concepts, define them clearly, and provide illustrative examples.
- Present information in a well-organized and visually appealing manner using HTML tags.
- Optimize the learning experience by converting detailed content into digestible formats.
Elaboration and Examples
- Delve deeper into the concepts to provide a comprehensive understanding.
- Explain theoretical ideas with real-world scenarios for better comprehension.
- Use examples to illustrate how theoretical concepts apply in practical situations.
- Ensure that explanations are detailed but easy to grasp for the audience.
Ensuring Educational Rigor
- Maintain the academic integrity of the content while simplifying it for learners.
- Structure content with HTML tags like
<li>,<ul>, and<p>appropriately. - Create visually appealing educational materials to enhance the learning process.
- Keep the HTML output organized and easy to navigate for better understanding.
Direct Proportion
- When two variables are directly proportional, one variable being zero means the other is also zero. As one variable increases, the other increases at the same rate. This relationship results in a straight-line graph passing through the origin.
- Direct proportionality implies that the variables move in the same direction and by the same proportion. If one variable increases or decreases, the second variable changes at the same rate. For instance, if a value is multiplied by 10, the other value is also multiplied by 10. The general equation for direct proportionality is expressed as a direct ratio.
- An illustrative example of direct proportion is the relationship between speed and time. If the speed of a car doubles, the time it takes to travel a certain distance is halved.
Graphical Representation of Direct Proportion
- A direct proportional graph is represented by a straight line passing through the origin (0,0). This point is crucial as it serves as the reference point for the coordinate system.
- Plotting three coordinates is sufficient to draw a direct proportional graph, showcasing the linear relationship between the variables.
Inverse Proportion
- In inverse proportionality, two variables have a product that remains constant. For instance, when the area of a rectangle is fixed at 20 cm², the length and width will always multiply to give 20.
- As one variable increases in an inverse relationship, the other decreases at the same rate. For example, if one value is multiplied by 10, the other value is divided by 10.
- An application of inverse proportionality can be seen in the relationship between the number of workers and the time taken to complete a task. More workers result in less time needed to finish the work.
Graphical Representation of Inverse Proportion
- An inverse proportional graph is depicted as a curve, approaching the axes as the variables reach extreme values.
- Unlike direct proportion, an inverse proportional graph requires more points to accurately represent the relationship between the variables due to the curved nature of the graph.
Coordinates in Graphs
- Coordinates in graphs represent the ordered pair of numbers (x, y) defining the position of a point in a coordinate system.
- For direct proportional graphs, three coordinates are typically plotted to showcase the linear relationship between the variables.



























| Image caption |
| Back to top |
How to recognize whether graphs show direct or inverse proportion
- If a graph shows direct proportion:
- The graph is a straight line
- The line goes through the origin (0, 0)
- For any coordinate, the relationship between x and y is constant
- The equation of the line has the general form



- If a graph shows inverse proportion:
- The graph is a curve
- The curve does not cross either axis
- For any coordinate, the product of x and y is always the same
- The equation of the curve has the general form for each coordinate






Examples
Image gallerySkip image gallery- Image caption, Explain why this graph shows direct proportion.



- Image caption, A graph showing direct proportion is a straight line that passes through the origin (0, 0).
- Image caption, Some of the coordinates of the graph are shown: (0, 0), (4, 20), (5, 25) and (8, 40). These points can be used to show that x and y are directly proportional.
- Image caption, Some of the coordinates of the graph are shown: (0, 0), (4, 20), (5, 25) and (8, 40). These points can be used to show that x and y are directly proportional.


Understanding Direct and Inverse Proportions
Direct proportion refers to a relationship where the ratio of two variables remains constant. In a direct proportion graph, such as y = 5x, the y-value is always five times the x-value. This concept is visually depicted in the graph where the coordinates follow the pattern (x, 5x).
Example of Direct Proportion:
- When x is 4, y is 20 (4:20 = 1:5)
- When x is 5, y is 25 (5:25 = 1:5)
- When x is 8, y is 40 (8:40 = 1:5)
In contrast, inverse proportion showcases a relationship where the product of two variables remains constant. As x increases, y decreases in such a way that their product stays the same. This is represented by a curve in the graph that doesn't intersect either axis.
Example of Inverse Proportion:
- 1 x 12 = 12
- 2 x 6 = 12
- 3 x 4 = 12
- 4 x 3 = 12
- 6 x 2 = 12
- 12 x 1 = 12
The inverse proportion graph illustrates that as x increases, y decreases in a corresponding manner, maintaining their inverse relationship.
Key Takeaways
| Direct Proportion | Inverse Proportion |
|---|---|
| Ratio remains constant | Product remains constant |
| y = nx | xy = constant |
Graphs Showing Proportional Relationships
In graphs that depict inverse proportionality, the curve does not intersect either axis. For instance, at the point (40, 0.3), although it might seem like the point intersects the axis, it is actually plotted above it.
- When examining inverse proportion graphs, the plotted points may appear close to the axis without touching it, as exemplified by the point (40, 0.3) above the y-axis. Even as the curve approaches the axis, it will never touch it. An increase in x-values results in a decrease in y-values, maintaining the product constant at 12.
Illustrative Examples
- Consider a magnified view of the point (40, 0.3) showcasing that it does not touch the x-axis. The product of x and y values, such as 6 * 2 = 12, 40 * 0.3 = 12, and 1200 * 0.01 = 12, remains constant.
Direct Proportion Graphs
Directly proportional graphs display a straight line from the origin, indicating a direct relationship between the variables.
Example Scenario
- An example graph with y increasing in twenties and x in fives showcases direct proportionality. The straight diagonal line from the point of intersection illustrates this relationship.
| Slide Number | Content |
|---|---|
| 1 of 8 | Example 1: A graph with y in twenties to forty and x in fives to ten. A direct proportionality is shown by a straight line from the intersection point. |
| 1 of 8 | Example 1: A graph with y in twenties to forty and x in fives to ten. A direct proportionality is shown by a straight line from the intersection point. |
How to Draw a Direct Proportion Graph Using Real-Life Data
- Identify the relationship between the variables.
- Create a table of values based on the identified ratio. The initial point is always (0, 0). One point replicates the given ratio. Multiply to determine at least one additional point. While three points are necessary, more can be included.
- The first point is always (0, 0).
- Another point reflects the established ratio.
- Multiply to obtain at least one more point.
- Three points are essential, but more can be added.
- Plot the points on the graph.
- Draw a straight line passing through the points and the origin (0, 0).
Examples
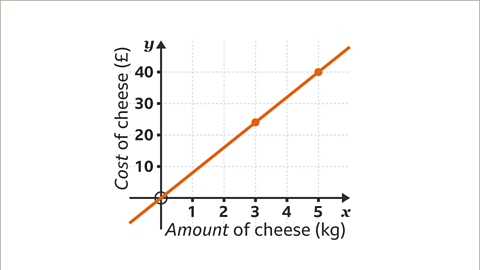
- For instance, if 1 kilogram of cheese costs £8, the graph depicts the amount of cheese (𝑞) against the cost (𝑝), considering costs for up to 5 kilograms of cheese.

1 kilogram of cheese costs £8. The graph illustrates the relationship between the amount of cheese (𝑞) and its cost (𝑝), showing costs for up to 5 kilograms of cheese.
The Relationship between Amount and Cost of Cheese
- The cost of cheese is directly tied to the amount you purchase. For every kilogram of cheese, the cost is £8. This means that the ratio of the amount of cheese to its cost is always 1:8.
- To illustrate this relationship, we can create a table of values to represent different amounts of cheese and their corresponding costs:
Amount of Cheese (kg) Cost (£) Coordinates (x, y) 0 0 (0, 0) 1 8 (1, 8) 2 16 (2, 16) 3 24 (3, 24) 4 32 (4, 32) 5 40 (5, 40) - By plotting these values on a graph, we can see a direct proportion between the amount of cheese and its cost. Each point falls on a straight line, demonstrating the relationship clearly.
Graphical Representation of the Relationship
- The graph visually depicts how the cost of cheese increases with the amount purchased. The x-axis represents the amount of cheese in kilograms, ranging from 0 to 5, while the y-axis represents the cost in pounds, ranging from 0 to 40.
- Each point on the graph corresponds to a specific amount of cheese and its cost. The plotted points align in a straight line, showcasing the direct proportionality between the two variables.
Direct Proportion Graphs
- Image caption: A direct proportion graph results in a straight line. It always passes through the origin. Three points are typically used to plot a correct line.
- Image caption: Illustration showing a direct proportion graph with two points plotted at (3 kg, 24 pounds) and (5 kg, 40 pounds).


Direct Proportion Relationship Example
- Image caption: Consider the relationship where 5 miles equate to approximately 8 kilometers. Create a graph to depict this direct proportionality.
- Image caption: Example illustrating the equivalence of five miles to eight kilometers.


Direct Proportionality Illustration
- Image caption: In a direct proportion between distance in miles and distance in kilometers, the ratio is consistently 5:8. The origin point is (0, 0), and the point (5, 8) represents the equivalence of 5 miles to 8 kilometers.
- Image caption: Diagram displaying a table with highlighted values showcasing the direct proportionality between miles and kilometers.
Distance in miles (X) Distance in kilometers (Y) Coordinates (X, Y) 0 0 (0, 0) 5 8 (5, 8) 10 16 (10, 16) 50 80 (50, 80) 

Image caption
- The maximum distance in miles is 50 miles. The x-axis (horizontal axis) should extend up to 50. The highest distance in kilometers is 80. The y-axis (vertical axis) should extend up to 80.
- Image caption: Points are plotted, forming a straight line. Connect the points to complete the graph. Graphs can help in converting between miles and kilometers.


Question
- One kilogram of cheese is equivalent to eight pounds. If 1 kg of cheese costs £8, sketch a graph showing the quantity of cheese (x-axis) against the cost (y-axis) for up to 5 kg of cheese.


How to Draw a Graph for Inverse Proportion
To draw a graph for inverse proportion:
- Identify the constant product of the variables:
- Draw a table of values to complete the graph:
When two quantities are inversely proportional, their product remains constant. For instance, if one number is multiplied by another, such as 4 multiplied by 5 resulting in 20 (4 x 5 = 20), this product remains the same despite changes in the variables.
To construct a graph for inverse proportion, it is essential to create a table of values representing factor pairs of the constant product. Factor pairs are two numbers that, when multiplied together, yield a specific whole number. For example, 3 and 4 form a factor pair of 12 since 3 x 4 = 12. Each pair of factors will share the same product. Multiple coordinates are necessary as the graph typically forms a curve.

Factor Pair
Two numbers that, when multiplied together, result in a specific whole number. For instance, if we take the number 12, the pair of numbers 3 and 4 can be multiplied to give 12, making them a factor pair of 12. It's important to note that a whole number can have multiple factor pairs.
Characteristics of Factor Pairs:
- Each pair will have the same product.
- When dealing with curves, several coordinates are necessary.
Steps to Identify and Use Factor Pairs:
- Determine all possible factor pairs by finding numbers that multiply to the given whole number.
- Identify pairs that yield the same product.
- For graphical representations, plot the coordinates derived from these factor pairs.
Graphing a Rectangle with Fixed Area
- When plotting the graph of a rectangle with a fixed area, such as 24 cm², it is essential to draw a smooth curve through the points.
- For instance, consider a rectangle with an area of 24 cm². To graph the length of the rectangle against its width, plot the points accordingly.
Factor Pairs and Coordinates
- For a rectangle with an area of 24 cm², the product of its length and width is always 24. To generate coordinates, list the factor pairs of 24.
- Factor pairs of 24 include: (1, 24), (2, 12), (3, 8), (4, 6), (6, 4), (8, 3), (12, 2), and (24, 1).
Creating a Table of Values
- To accurately represent the relationship between length and width, a table of values can be created using the factor pairs of 24 as coordinates.
- The table includes values such as: (1, 24), (2, 12), (3, 8), (4, 6), (6, 4), (8, 3), (12, 2), and (24, 1).
Graph Representation
- The largest factor of 24 is 24. When plotting the graph, both the length and width axes extend up to 24 units.
- Visualize the graph with the y-axis representing width and the x-axis representing length, each going up in intervals to 24.
Image caption, Plot the coordinates
- Image caption, Plot the coordinates.
- Image caption, Draw a smooth curve through the plotted points.


Question
Paraphrase the information given, elaborate and explain with examples wherever required. Give all points in bullet format with proper heading across (add li tag to html of bullet points). Make sure you do not miss any topic. Make sure not more than 2 headings have an HTML tag H7 and not more than 4 Subheadings have an HTML tag H8 otherwise make the headings bold. Make sure everything is paraphrased and in detail and keep the language easy to understand.
Slide 1 of 6 , Example 1: A diagram showing a rectangle shaded orange and labelled Area equals twenty-four centimeters squared.
A rectangle has a fixed area of 24 cm². Draw the graph of the length of the rectangle (𝑤) against its width (ℓ).
Subheading 1
- Point 1
- Point 2
Subheading 2
- Point 3
- Point 4
1 of 6
Slide 1 of 6 , Example 1: A diagram showing a rectangle shaded orange and labelled Area equals twenty-four centimeters squared. A rectangle has a fixed area of 24 cm². Draw the graph of the length of the rectangle (𝑤) against its width (ℓ).Back to topPractise drawing direct and inverse proportion graphs
Practise drawing direct and inverse proportion graphs in this quiz. You may need a pen and paper to complete these questions.
Quiz
- Understand the concept of direct and inverse proportion in graphs.
- Practice drawing direct proportion graphs with various examples.
- Practice drawing inverse proportion graphs with different scenarios.
- Ensure you use a pen and paper to plot these graphs accurately.
Game - Divided Islands
- Explore the concept of division using the game "Divided Islands".
- Understand how division can be visually represented in a game scenario.
- Apply division concepts to solve problems within the game.
- Engage with the game to reinforce your understanding of division.

|
Explore Courses for Year 7 exam
|

|