Olympiad Notes: Playing With Numbers | Maths Olympiad Class 6 PDF Download
| Table of contents |

|
| Introduction |

|
| Factors |

|
| Multiples |

|
| Prime Numbers |

|
| Composite numbers |

|
| Tests for divisibility of numbers |

|
| Highest Common Factor |

|
| Lowest Common Multiple (LCM) |

|
Introduction
John‘s uncle gave him 24 muffins to distribute among his friends. This means john has 24 ÷ 1 = 24 muffins. He wants to equally distribute it among 6 children. How will he do that?
He wants to equally distribute it among 6 children. How will he do that?  24 ÷ 6 = 4 i.e. 24 = 6 x 4 Now what if 2 more children come to his place? How will he distribute the same number of muffins among 8 children?
24 ÷ 6 = 4 i.e. 24 = 6 x 4 Now what if 2 more children come to his place? How will he distribute the same number of muffins among 8 children? 24 ÷ 8 = 3
i.e. 24 = 8 x 3
Suppose 4 more children visit his place at the same time. Can he distribute 24 muffins equally among all children?
Yes, he can!!! 24 ÷ 12 = 2 i.e .24 = 12 x 2
From this calculation we can see that 24 can be written as a product of two numbers in different ways as 24 = 6 × 4; 24 = 8 × 3; 24 = 12 × 2.
This means 2, 3, 4, 6, 8 and 12 are exact divisor of 24. They are known as factors of 24.
Factors
A factor of a number is defined as the number which is an exact divisor of that number.
- Suppose we want number 12.
- Think about the numbers you can multiply together to get 12. 3 x 4 = 12 ; 2 x 6 = 12 ; 1 x 12 = 12
- This shows that 1, 2, 3, 4, 6 and 12 are factors of 12.
Facts about factors
- The number 1 and the number itself are always factors of that number.
- Every factor is less than or equal to the given number.
- Every factor of a number divides the given number exactly.
- The number of factors of a given number are finite.
Common Factors
When two (or more) numbers have the same factor, that factor is known as a common factor.
Let’s find put common factors of 6 and 18.
6 = 1 x 6, 6 = 2 x 3, therefore, factors of 6 = 1, 2, 3, 6 18 = 1 x 18,
18 = 2 x 9, 18 = 3 x 6, therefore, factors of 18 = 1, 2, 3, 6, 9, 18.
The numbers which appear in both the list are: 1, 2, 3, 6.
Hence, common factors of 6 and 18 are 1, 2, 3 and 6.
Example: Write all the factors of the following numbers:
(a) 23
(b) 36
Sol: (a) 23 = 1, 23
(b) 36 = 1 x 36,
36 = 2 x 18,
36 = 3 x 12,
36 = 4 x 9
36 = 6 x 6
Therefore, factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18 and 36.
Perfect number
A perfect number is defined as a number for which sum of all its factors is equal to twice the number.
For eg: (i) The factors of 6 are 1, 2, 3 and 6,
1 + 2 + 3 + 6
= 12
= 2 x 6.
Therefore, 6 is a perfect number.
(ii) The factors of 496 are 1, 2, 4, 8, 16, 31, 62, 124, 248
1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 + 496
= 992
= 2 x 496.
Therefore, 496 is a perfect number.
Multiples
A multiple of a number is any whole number obtained by multiplying that number by another whole number.
For example, the multiples of 3 are 3, 6, 9, 12, 15, 18 and so on.
Every multiple of a number is greater than or equal to that number. The number of multiples of a given number is infinite. Every number is a multiple of itself.
Properties of Multiples
(i) Every number is a multiple of 1.
For eg: 7 x 1 = 7,
9 x 1 = 9.
(ii) Every number is the multiple of itself.
For eg: 1 x 7 = 7
1 x 21 = 21
(iii) Zero (0) is a multiple of every number.
For eg: 0 x 9 = 0,
0 x 11 = 0.
(iv) Every multiple except zero is either equal to or greater than any of its factors.
For eg: multiple of 7 = 7, 14, 28, 35, 77, …………., etc.
(v) The product of two or more factors is the multiple of each factor.
For eg: 3 x 7 = 21. So, 21 is the multiple of both 3 and 7.
(vi) There is no end to multiples of a number.
5, 10, 15, 20, 25, …………….., 100, 105, 110, …………………., are the multiples of 5.
Example: List the first 5 multiples of 5, 8 and 9.
Sol: First 5 multiples of 5 are : 10, 15, 20, 25, 30
First 5 multiples of 8 are : 8, 16, 24, 32, 40
First 5 multiples of 9 are: 9, 18, 27, 36, 45
Common Multiples
The Common multiples of two or more numbers are the multiples that are common to every given number.
Let’s find the common multiples of 4 and 6. 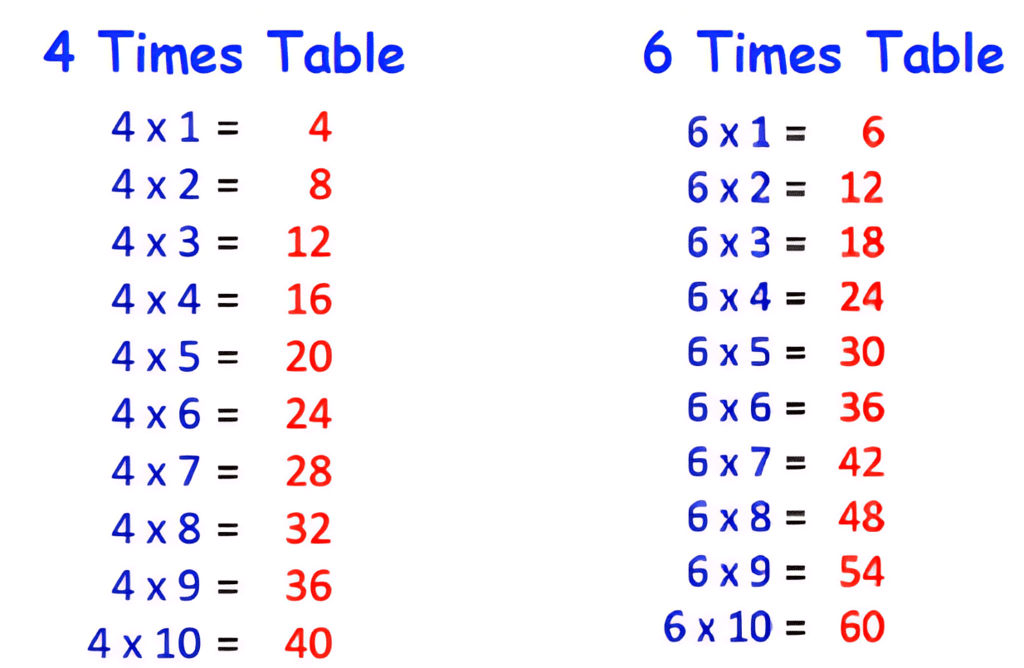
- First 10 multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40.
- First 10 multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60.
- The common numbers which appear in both the list are 12, 24 and 36.
- Therefore, the common multiples of 4 and 6 are 12, 24 and 36.
Example: Find all the multiples of 9 upto 100.
Sol: Multiples of 9 = 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99.
Prime Numbers
The numbers other than 1 whose only factors are 1 and the number itself are called prime number.
For eg: 5 = 1 x 5, 23 = 1 x 23
Properties of Prime Numbers
- A prime number is a whole number greater than 1.
- It has exactly two factors, that is, 1 and the number itself.
- There is only one even prime number, that is, 2.
- Any two prime numbers are always co-prime to each other.
- Every number can be expressed as the product of prime numbers.
Co-prime numbers
Any set of numbers which do not have any other common factor other than 1 are called co-prime or relatively prime numbers.
For example: Factors of 5 = 1, 5 Factors of 6 = 1, 2, 3, 6. This shows that 5 and 6 have no common factor other than 1. Therefore, they are co-prime numbers.
Properties of co-prime numbers
- All prime numbers are co-prime to each other.
- Any consecutive whole numbers are always co-primed.
- Sum of any two co-prime numbers is always co-primed.
- Co-prime numbers need not to be prime numbers.
Twin primes
Twin primes are a pair of primes which differ by 2.
First few twin primes are E.g. (3, 5); (5, 7); (11, 13); (17, 19); (29, 31); (41, 43)
Example : Express 44 as the sum of two odd primes.
Sol: 44 = ____ + ____.
Here we have to find 2 numbers which are odd as well as prime numbers and whose sum is 44.
Odd prime numbers upto 44 are 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43.
Now let’s find out a pair of numbers whose sum is 44.
Sum of 3 and 41 is 44. So, 44 = 3 + 41.
Composite numbers
A composite number is defined as a number having more than two factors.
For eg: (i) Factors of 9 are 1, 3 and 9. Therefore it is a composite number.
(ii) Factors of 14 are 1, 2, 7 and 14. Therefore it is a composite number.
Note:
(i) 1 is neither prime nor composite number.
(ii) Any whole number greater than 1 is either a prime or composite number.
Prime Numbers v/s Composite Numbers
Example 1: Write seven consecutive composite numbers less than 100 so that there is no prime number between them.
Sol: 89 and 97 are the prime numbers. 90, 91, 92, 93, 94, 95, 96 lies in between 89 and 97. All these numbers have more than 2 factors. Therefore, all the numbers are composite numbers.
Example 2: Write down separately the prime and composite numbers less than 20
Sol: (i) Prime Numbers less than 20 are 2, 3, 5, 7, 11, 13, 17, 19
(ii) Composite Numbers less than 20 are 4, 6, 8, 9, 10, 12, 14, 15, 16, 18.
Tests for divisibility of numbers
Divisibility by 2
- If the number ends with 2, 4, 6, 8 or 0, it is divisible by 2.
- Example: 28, 54, 96 Here 28, 54 and 96 ends with 8, 4 and 6 respectively.
- Therefore, 28, 65 and 96 are divisible by 2.
Divisibility by 3
- If the sum of the digits of any number is divisible by 3 then that number is divisible by 3.
- Example: 429; 4 + 2 + 9 = 15 ; 15 ÷ 3 = 5.
- Therefore, 429 is divisible by 3.
Divisibility by 4
- If the last 2 digits of any number are divisible by 4, then that number is divisible by 4.
- Example: 628; Last 2 digits are 28 and 28 ÷ 4 = 7.
- Therefore, 628 is divisible by 4.
Divisibility by 5
- If the digit in the ones place of a number is 5 or 0, then it is divisible by 5.
- Example: (i) 95 ends in 5; Therefore, 95 is divisible by 5.
(ii) 680 ends in 0. Therefore, 680 is divisible by 5.
Divisibility by 6
- If a number is divisible by 2 and 3, then that number is divisible by 6.
- Example: 246. It is divisible by 2 as it ends with 6. Now, 2 + 4 + 6 = 12. 12 is divisible by 3, so 246 is divisible by 3 also.
- This shows that 246 is divisible by 2 and 3.
- Therefore, 246 is divisible by 6.
Divisibility by 8
- A number is divisible by 8 if the number formed by its last three digits is divisible by 8.
- Example: 2544. Here, last 3 digits are 544.
544 ÷ 8 = 68 - Therefore, 2544 is divisible by 8.
Divisibility by 9
- A number is divisible by 9 if the sum of its digits is divisible by 9.
- Example: 42,471.
Here, 4 + 2 + 4 + 7 + 1 = 18 is divisible by 9. - Therefore 42,471 is divisible by 9.
Divisibility by 10
- A number is divisible by 10 if it ends with a ZERO.
- Example: 1570. Here the last digit is 0.
- Therefore, 1570 is divisible by 10.
Divisibility by 11
- A number is divisible by 11 if the difference of the sums of the alternate digits is 0 or a multiple of 11.
- Example: (i) 9724
9 + 2 = 11.
7 + 4 = 11.
Difference between the two sums is 0. Therefore, 9724 is divisible by 11.
(ii) 45958
4 + 9 + 8 = 21
5 + 5 = 10
Here, 21 – 10 = 11. This is a multiple of 11. Therefore, 45958 is divisible by 11.
Some More Divisibility Rules
- If a number is divisible by another number, it's also divisible by each of the factors of that number.
Example: 72 is divisible by 18, and since the factors of 18 are 1, 2, 3, 6, 9, and 18, 72 is divisible by each of these factors. - If a number is divisible by two co-prime numbers, it's also divisible by their product.
Example: If 90 is divisible by 5 and 9 (co-prime numbers), it's also divisible by their product, which is 45. - If two given numbers are divisible by a number, then their sum is also divisible by that number.
Example: If 21 and 18 are divisible by 3, then their sum, 39, is also divisible by 3. - If two given numbers are divisible by a number, then their difference is also divisible by that number.
Example: If 58 and 54 are divisible by 2, then their difference, 4, is also divisible by 2.
Example: A number is divisible by both 5 and 12. By which other number will that number be always divisible?
Sol: The number is divisible by 5 and 12.
Since 5 and 12 are co-prime numbers so the number must be divisible by the product 5 × 12 = 60.
So, the given number will always be divisible by 60.
Highest Common Factor
(HCF) of two or more given numbers is the highest (or greatest) of their common factors. It is also known as Greatest Common Divisor (GCD).
To find the HCF of two or more numbers, we can use any of the following method.
(i) Common factor method
(ii) Prime factorization method
Common factor method
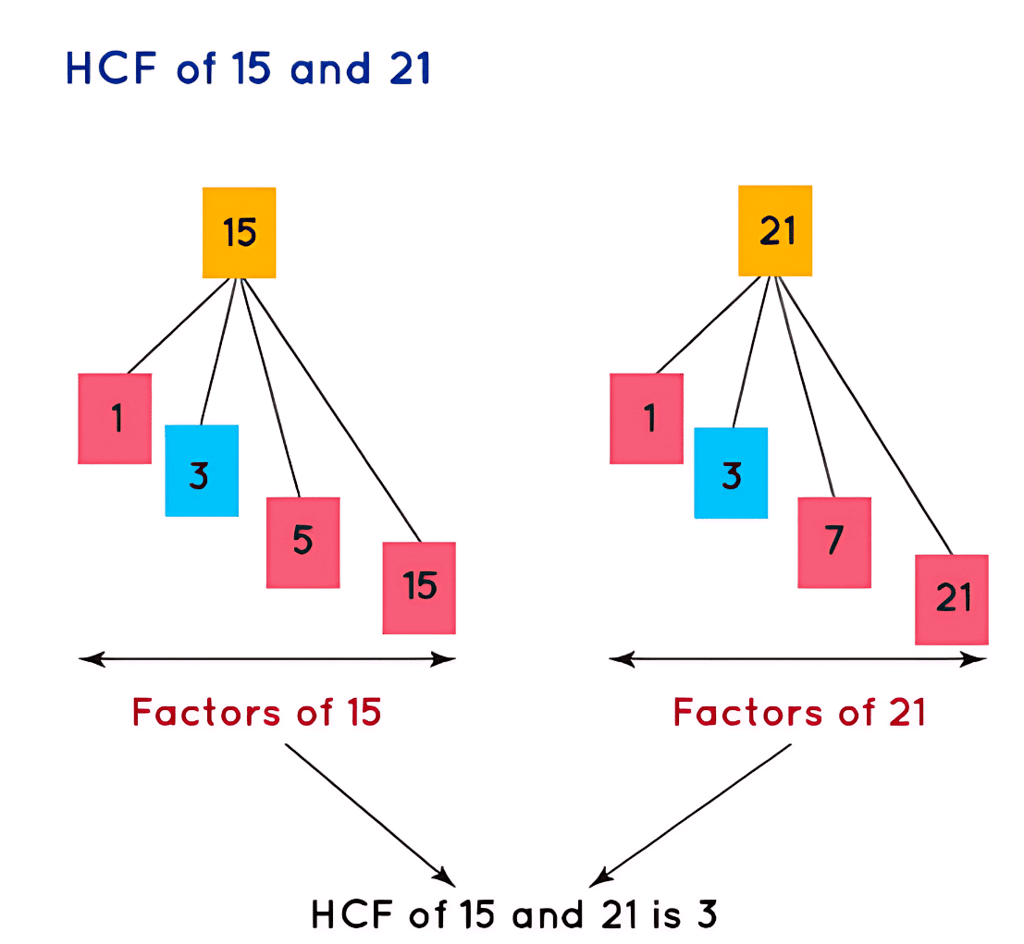
- Let’s find the HCF of 15 and 21.
- First find all factors of the given numbers individually.
- Factors of 15 = 1, 3, 5, 15
Factors of 21 = 1, 3, 7, 21 - Therefore, common factors of 15 and 21 are 1 and 3.
- HCF of 15 and 21 is 3.

Prime factorization method
Let’s find the HCF of 27 and 45.
- First we have to find the factors of 27.
- Write a pair of factors. 27 = 3 x 9.
- Now further factorize the composite factor 9 as 3 and 3.
- Repeat the process till you get the prime factors of all the composite factors.

- Since 3 is a prime number we cannot factorize it further.
Therefore, 27 as a product of its prime factors is written as 27 = 3 x 3 x 3 - Let’s find the factors of 45.
- Write a pair of factors. 45 = 5 x 9.

- Further factorize the composite factor 9 as 3 and 3.
- Therefore, 45 as a product of its prime factors is written as 45 = 5 x 3 x 3.
- Multiply all the factors which appear in both the list.
27 = 3 x 3 x 3
45 = 3 x 3 x 5
i.e 3 x 3 = 9. - Therefore, HCF of 27 and 45 is 9.
Ques: Find the HCF of the following numbers. 18, 54, 81
Sol: Let’s find the HCF by prime factorization method. 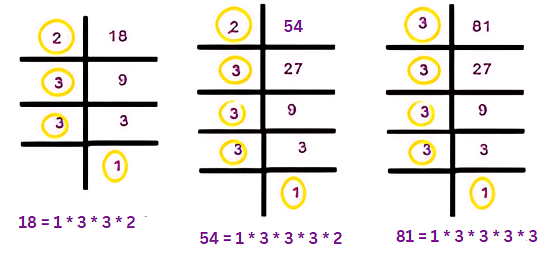 18 = 2 x 3 x 3
18 = 2 x 3 x 3
54 = 2 x 3 x 3 x 3
81 = 3 x 3 x 3 x 3
Multiply all the factors which appear in both the list. i.e 3 x 3 = 9.
The HCF of 18, 54 and 81 is 9.
Lowest Common Multiple (LCM)
- The Lowest Common Multiple (LCM) of two or more given numbers is the lowest (or smallest or least) of their common multiples.
- If two numbers are co-prime then the LCM is the product of the two numbers.
Example: LCM of 7 and 13.
7 = 7 x 1
13 = 1 x 13.
So, LCM is 7 x 13 = 91.
Common multiple method
Let's find out lowest common multiple of the numbers 8, 12 and 18.
- List the multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88.
- List the multiples of 12: 12, 24, 36, 48, 60, 72, 84.
- List the multiples of 18: 18, 36, 54, 72, 90, 1.
- The common multiples of 8, 12 and 18 are 72 ...
- L.C.M. of 8, 12 and 18 is 72.
This method works only when there are very small numbers.
Prime factorization method
Let's find out the LCM of 90, 100 and 150.
- Prime factorisation of the given numbers:
90 = 2 x 3 x 3 x 5 = 2 x 3 x 5
100 = 2 x 2 x 5 x 5 = 2 x 5
150 = 2 x 3 x 5 x 5 = 2 x 3 x 5 - Let’s find the product of all the factors with highest powers.
2 x 3 x 5 = 4 x 9 x 25 = 900.
Common division method of Prime Factorisation
A very convenient method to find the LCM is the common division method.
In this method of prime factorisation we proceed as follows:
- Arrange all the given numbers in a row and separated by commas.
- Start with the lowest prime number which divides at least one of the given numbers exactly.
- Write down the quotients and any undivided numbers in the next line.
- Repeat the process as shown below until 1 is the only common factor.
- Find the product of all the divisors.
- This is the required LCM.
Example 1 : Find the L.C.M. of the numbers 36, 48 and 72.
Sol: LCM = 2 x 2 x 2 x 2 x 3 x 3 = 144 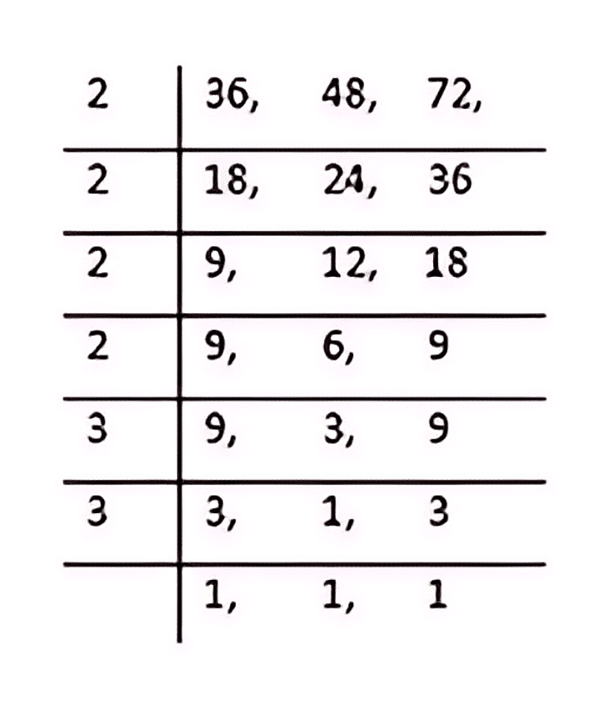
Example 2: Find the least number which when divided by 18, 28, 32 and 42 leaves a remainder 5 in each case.
Sol: First we should find the LCM of 18, 28, 32 and 42. 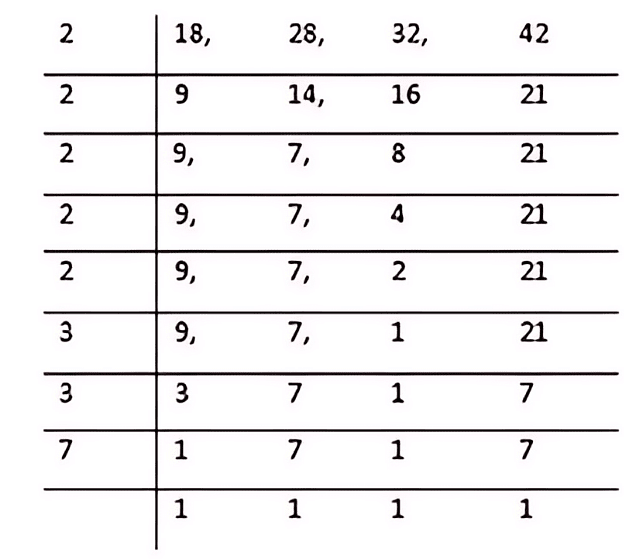
LCM = 2 x 2 x 2 x 2 x 2 x 3 x 3 x 7 = 2016
2016 is the least number which when divided by the given numbers will leave remainder 0 in each case. But we need the least number that leaves remainder 5 in each case.
Therefore, the required number is 5 more than 2016 i.e. 2016 + 5 = 2021.
|
8 videos|98 docs|60 tests
|
FAQs on Olympiad Notes: Playing With Numbers - Maths Olympiad Class 6
| 1. What are prime numbers and how are they different from composite numbers? |  |
| 2. How do you find the highest common factor of two numbers? |  |
| 3. What is the importance of the lowest common multiple (LCM) in mathematics? |  |
| 4. How can you determine if a number is a multiple of another number? |  |
| 5. What are some common tests for divisibility of numbers that can help in simplifying calculations? |  |

|
Explore Courses for Class 6 exam
|

|