Notes: Number System | Mathematics & Pedagogy Paper 2 for CTET & TET Exams - CTET & State TET PDF Download
Introduction to Number System
The Number System is the foundation of mathematics and plays a crucial role in arithmetic operations, problem-solving, and logical reasoning. Understanding numbers and their properties is essential for developing strong mathematical skills, especially for teaching primary and upper-primary students.
In competitive exams like CTET and State TETs, this chapter holds significant weightage, with 3 to 5 questions typically appearing in each exam. Mastering this topic will not only enhance conceptual clarity but also improve problem-solving speed and accuracy.
What is a Number?
A number is a mathematical representation that consists of a set of digits. Numbers can be expressed in two forms: in words and in figures. For example, the number 3290 can be written in words as "three thousand two hundred ninety."
There are three types of system to write down a number which are as follows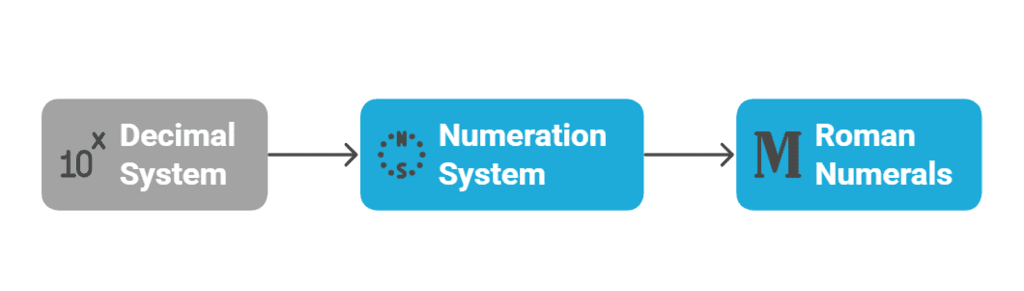
Decimal System
The Decimal System is based on ten symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9, which are known as digits. This system is widely used both in India and internationally for numerical representation and calculations.
Numeration System
There are mainly two systems of numeration: the Indian system and the International system.
1. Indian (Hindu-Arabic) System
In this system, we write the digits of the number from the bottom (ones) to the top (crore). For example, consider the number 35,678,932.
| Periods | In words | In Figures | In Powers | Numbers |
|---|---|---|---|---|
| Crore | Ten Crore | 100,000,000 | 108 | 0 |
| Crore | One Crore | 10,000,000 | 107 | 3 |
| Lakh | Ten Lakh | 1,000,000 | 106 | 5 |
| Lakh | One Lakh | 100,000 | 105 | 6 |
| Thousand | Ten Thousand | 10,000 | 104 | 7 |
| Thousand | One Thousand | 1,000 | 103 | 8 |
| Ones | Hundred | 100 | 102 | 9 |
| Ones | Ten | 10 | 101 | 3 |
| Ones | One | 1 | 100 | 2 |
According to the Indian system, the number 35,678,932 is read as "three crore fifty-six lakh seventy-eight thousand nine hundred thirty-two".
2. International System of Numeration
In the International System, we write the digits of a number from the bottom (ones) to the top (millions). For example, consider the number 35,678,932. The breakdown of this number is as follows:
| Periods | In Words | In Figures | In Powers |
|---|---|---|---|
| Million | Hundred million | 108 | 0 |
| Million | Ten million | 107 | 3 |
| Million | Million | 106 | 5 |
| Thousand | Hundred thousand | 105 | 6 |
| Thousand | Ten thousand | 104 | 7 |
| Thousand | Thousand | 103 | 8 |
| Ones | Hundred | 102 | 9 |
| Ones | Ten | 101 | 3 |
| Ones | One | 100 | 2 |
The number 35,678,932 is read as thirty-five million six hundred seventy-eight thousand nine hundred thirty-two.
Examples
Example 1
Convert the following numbers into figures:
- Three crore twenty-four lakh one thousand ten
- Six million seven thousand thirty-seven
Solution:
(i) 3 × 107 + 2 × 106 + 4 × 105 + 1 × 103 + 10 = 30,000,000 + 2,000,000 + 400,000 + 1,000 + 10 = 3,24,01,010
(ii) 6 × 106 + 7× 103 + 3 × 101 + 7 = 6,000,000 + 8,000 + 30 + 7 = 6,007,037
Example 2
Write the number 865,421 in word form in both the Indian and International systems.
Solution:
Indian System: Eight lakh sixty-five thousand four hundred twenty-one.
International System: Eight hundred sixty-five thousand four hundred twenty-one.
Face and Place Value of Digits in a Number
Face Value: The face value of a digit in a number is the value of the digit itself, regardless of its position. For example, in the number 92,347, the face value of 9 is 9, the face value of 2 is 2, the face value of 3 is 3, and so on.
Place Value: The place value of a digit depends on its position within the number. It is calculated as:
- Unit digit = (unit digit) × 100
- Ten digit = (ten digit) × 101
- Hundred digit = (hundred digit) × 102
- Thousand digit = (thousand digit) × 103
For example, in the number 4,354,972,375:
- 4 × 109 + 3 × 108 + 5 × 107 + 4 × 106 + 9 × 105 + 7 × 104 + 2 × 103 + 3 × 102 + 7 × 101 + 5 × 100
Thus, the place value of a digit depends on its location in the number. For instance, the face value of 5 remains five in both places, but its place values are 5 and 50,000,000.

Greatest and Lowest Numbers of n-digits
1. n-digit Greatest Number
The n-digit greatest number is formed by writing the digit 9 as many times as the value of n.
For example, the 5-digit greatest number is 99999.
2. n-digit Lowest Number
The n-digit lowest number is formed by writing the digit 1 followed by (n-1) zeros.
For example, the 5-digit lowest number is 10000.
Example
What is the difference between the 5-digit greatest number and the 6-digit smallest number?
- 1
- 9
- 11
- 99
Solution:
- 5-digit greatest number = 99999
- 6-digit smallest number = 100000
- Required difference = 100000 - 99999 = 1
Roman Numerals
The numbers we commonly use (e.g., 1, 2, 3, ...) are called 'Arabic Numbers'. Sometimes, we use another system called the Roman system. Roman numerals are occasionally used to denote the class (in which a student studies), the position of a candidate, on clock faces, in page numbering, etc.Roman Numerals Chart
| Roman | Arabic | Roman | Arabic |
|---|---|---|---|
| I | 1 | XIX | 19 |
| II | 2 | XX | 20 |
| III | 3 | XXX | 30 |
| IV | 4 | XL | 40 |
| V | 5 | L | 50 |
| VI | 6 | LXXV | 75 |
| VII | 7 | XC | 90 |
| VIII | 8 | C | 100 |
| IX | 9 | D | 500 |
| X | 10 | DI | 501 |
| XI | 11 | DXXX | 530 |
| XII | 12 | DL | 550 |
| XIII | 13 | DCCVII | 707 |
| XIV | 14 | DCCCXC | 890 |
| XV | 15 | CM | 900 |
| XVI | 16 | MD | 1500 |
Letters Used in Roman Numerals
- I = 1
- V = 5
- X = 10
- L = 50
- C = 100
- D = 500
- M = 1000
Characteristics of Roman Numerals
- Generally, a letter cannot be repeated more than three times. For example, I = 1, II = 2, III = 3, but 4 is not IIII; it is written as IV. Similarly, X = 10, XX = 20, XXX = 30, and XL = 40 (50 minus 10).
- In the repetition of Roman digits, the value of the Roman numeral is equal to the sum of the values of the individual digits. For example, III = 1 + 1 + 1 = 3, MM = 1000 + 1000 = 2000.
- V, L, and D cannot be repeated.
- I is subtracted only from V and X; X is subtracted only from L, M, and C; C is subtracted only from D and M. V, L, and D are not subtracted.
- If a smaller Roman symbol is to the left of a larger symbol, the value of the number is determined by subtracting the smaller symbol from the larger symbol. For example, XC = 100 - 10 = 90, CD = 500 - 100 = 400.
- If a smaller Roman symbol is to the right of a larger symbol, the value of the number is determined by adding both symbols. For example, XIII = 10 + 1 + 1 + 1 = 13, MD = 1000 + 500 = 1500.
- If a bar is placed over a number, its value is increased 1000 times. For example, IV = 4 × 1000 = 4000, D = 500 × 1000 = 500,000.
Example :
Convert the following numbers to Roman numerals:
- 45
- 60
- 90
- 96
- 225
- 625
Solution
- 45 → XLV
- 60 → LX
- 90 → XC
- 96 → XCVI
- 225 → CCXXV
- 625 → DCXXV
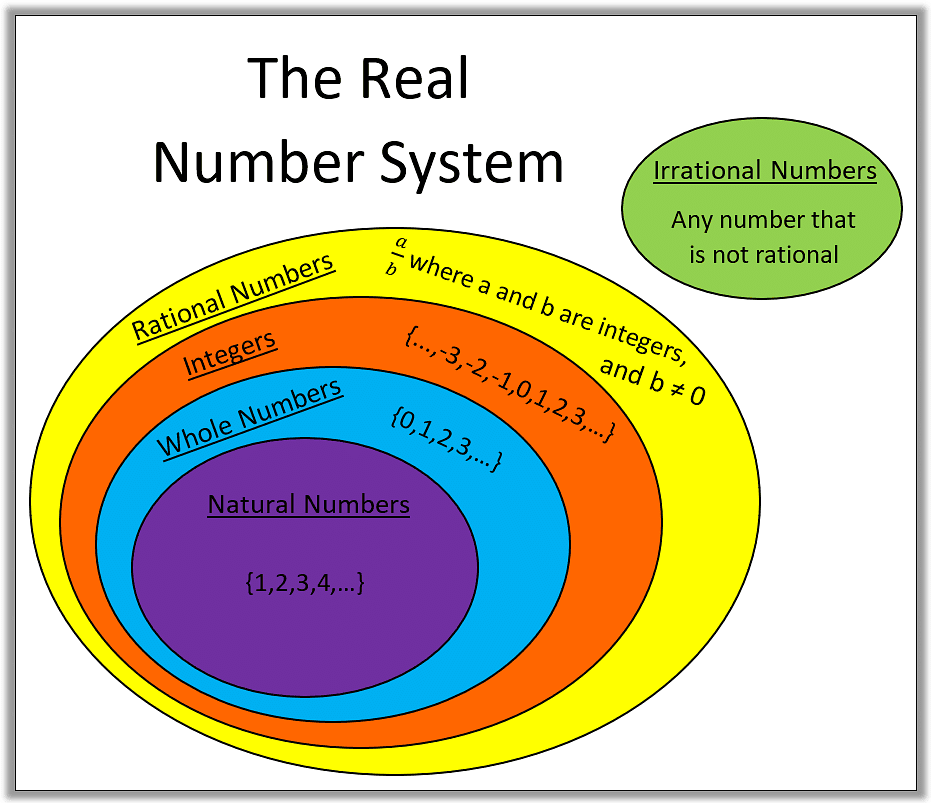
Classification of Numbers
Numbers are classified into different types based on their properties and usage in mathematics. This classification helps in understanding their behavior and applying them in calculations effectively. The key types include natural numbers, whole numbers, integers, prime numbers, and composite numbers.
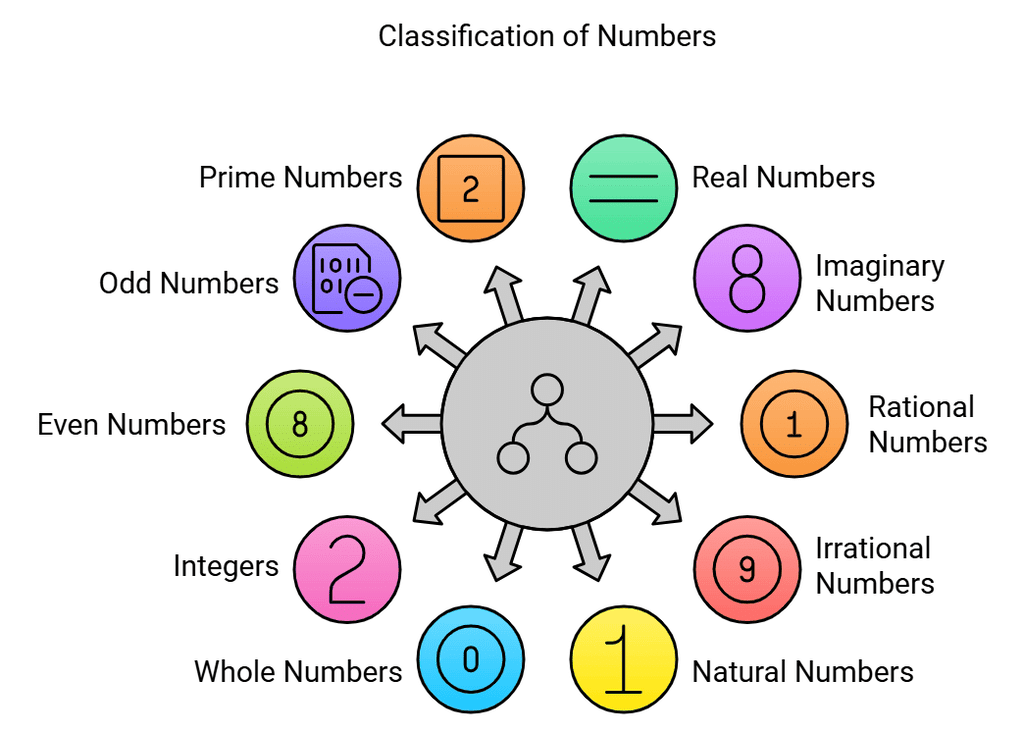
1. Real Numbers
Numbers that give a positive result when squared are called real numbers. This includes all positive, negative, rational, and irrational numbers. For example, 3 and √2 are real numbers.
2. Imaginary Numbers
Numbers that are not real are called imaginary numbers. When squared, these numbers yield negative values. For example, √-2 is an imaginary number.
3. Rational Numbers (or Fractions)
Numbers that can be expressed in the form of p/q, where p and q are integers and q ≠ 0, are called rational numbers. These are denoted by Q. Examples include 3/5, 4/9, and 2/7.
4. Irrational Numbers
Numbers that cannot be expressed in the form of p/q are called irrational numbers. Examples include √2, √3, and √5.
5. Natural Numbers
All consecutive counting numbers starting from 1 are called natural numbers. These are denoted by N. Examples include 1, 2, 3, 4, etc. Note that 0 is not a natural number.
6. Whole Numbers
All natural numbers, including zero, are called whole numbers. These are denoted by W. Examples include 0, 1, 2, 3, etc.
7. Integers
All positive and negative whole numbers are called integers. These are denoted by I. Examples include ..., -3, -2, -1, 0, 1, 2, 3, ...
- Positive Integers: Natural numbers are called positive integers. They are denoted by I+. Examples include 1, 2, 3, etc.
- Negative Integers: Negative of natural numbers are called negative integers. They are denoted by I-. Examples include -1, -2, -3, etc.
- Note: 0 is neither a positive nor a negative integer.
8. Even Numbers
A number that is completely divisible by 2 is called an even number. Examples include 8, 30, and 42. Note that the unit place of every even number will be 0, 2, 4, 6, or 8.
9. Odd Numbers
Numbers that are not divisible by 2 are called odd numbers. Examples include 1, 3, 5, 7, and 9.
10. Prime Numbers
A counting number that is exactly divisible by 1 and itself is called a prime number. Examples include 2, 3, 5, 7, 11, 13, 17, etc. Note that 2 is the smallest and only even prime number, and 1 is not a prime number.
There are 25 prime numbers between 1 and 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97.
11. Composite Numbers
A composite number has factors other than itself and unity, making it a non-prime number. Examples include 4, 6, 9, 14, and 15. Note that 1 is neither prime nor composite, and a composite number may be even or odd.
12. Coprime Numbers
Two natural numbers are called coprimes if they do not have any common factors other than 1. Examples include (2, 5), (7, 15), and (9, 13).
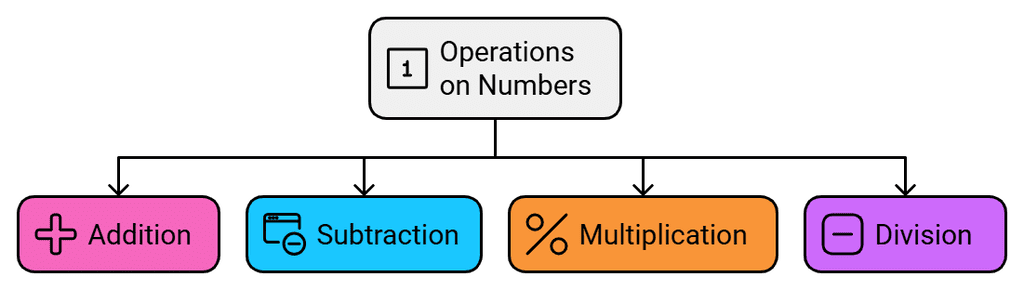
Operations on Numbers
Various operations on numbers include:
1. Addition
When two or more numbers are combined together, it is called addition, denoted by the sign ‘+’. For example:
52 + 76 + 87 = 215
2. Subtraction
When one or more numbers are taken out from a larger number, it is called subtraction, denoted by the sign ‘−’. For example:
139 - 12 - 60 = 67
3. Multiplication
When two numbers, say x and y, are multiplied together, x is added y times or y is added x times. It is denoted by the sign ‘×’. For example:
7 × 5 = 7 + 7 + 7 + 7 + 7 = 35
4. Division
Division is the method of finding how many times a given number, called the divisor, is contained in another given number, called the dividend. The quotient is the result, and the excess of the dividend over the product of the divisor and the quotient is called the remainder. For example:
362 ÷ 39
Divisor ← 39) 362 (9 → Quotient
351
11 → Remainder
These quantities are interrelated by the following relation:
Dividend = (Divisor × Quotient) + Remainder
Example: In a division sum, the quotient is 97, the remainder is 105, and the divisor is equal to the sum of the quotient and remainder. What is the dividend?
- 22000
- 19699
- 19800
- 19700
Solution: (2)
- Divisor = 97 + 105 = 202
- Dividend = 202 × 97 + 105 = 19699
- Hence, the dividend is 19699.
Example: Find the product of the 2nd natural number, the 2nd whole number, and the 2nd prime number.
- 0
- 4
- 6
- 7
Solution: (3)
- The 2nd natural number = 2
- The 2nd whole number = 1
- The 2nd prime number = 3
- Required product = 2 × 1 × 3 = 6
Properties of Operations on Numbers
Let a and b be two numbers. Then:
- Addition is commutative:a + b = b + a
For example: 930 + 56 = 986 and 56 + 930 = 986 - Subtraction is not commutative:a - b ≠ b - a
For example: 30 - 8 = 22 but 8 - 30 = -22 - Multiplication is commutative:ab = ba
For example: 22 × 32 = 704 and 32 × 22 = 704 - Division is not commutative: a ÷ b ≠ b ÷ a
For example: 25 ÷ 5 = 5 but 5 ÷ 25 = 0.2
Some Important Terms
- Additive Identity: When 0 (zero) is added to any number, we get the same number.
For any real number a: a + 0 = a
Hence, 0 is called the additive identity of a. - Additive Inverse: The number which, when added to the given number, gives the result as zero.
For any real number a: a + (-a) = 0
Hence, -a is called the additive inverse of a. - Multiplicative Identity: When 1 (one) is multiplied by any real number, we get the same number.
For any real number a: a × 1 = a
Hence, 1 is called the multiplicative identity of a. - Multiplicative Inverse: The number which, when multiplied by the given number, gives the result as 1.
For any real number a: a × (1/a) = 1
Hence, 1/a is called the multiplicative inverse of a.
Note: The multiplicative inverse is the same as the reciprocal of a number. - Associative Rule: For any three integers a, b, and c, the rule is defined as:
- (a + b) + c = a + (b + c)
- (a × b) × c = a × (b × c)
- Distributive Rule: For any three integers a, b, and c, the rule is defined as:
a × (b + c) = (a × b) + (a × c)
Example
Find the additive and multiplicative inverse of 3.
- -3, 1/3
- -3, -3
- 3, 1
- None of these
Solution: (1)
Additive inverse: 3 + (-3) = 0, hence -3 is the additive inverse of 3.
Multiplicative inverse: 3 × (1/3) = 1, hence 1/3 is the multiplicative inverse of 3.
Approximate Values
Sometimes, we use approximate values in various scenarios. For example, in a party, we estimate the number of guests. If a person's expenditure for a month is ₹1976, it can be approximated to ₹2000.
Approximating to the Nearest Ten
When rounding off a number to the nearest ten:
- Replace the unit digit by 0.
- If the digit in the ten's place is 5 or more, increase the ten's digit by 1; otherwise, leave it unchanged.
For example:
- Approximation of 542 is 540.
- Approximation of 7869 is 7870.
Approximating to the Nearest Hundred
When approximating a number to the nearest hundred:
- Replace the units and tens digits by 0.
- If the ten's digit in the original number is 5 or greater, increase the hundred's digit by 1; otherwise, leave it unchanged.
For example:
- Approximation of 5486 is 5500.
- Approximation of 89714 is 89700.
We can also approximate to thousand, ten thousand, etc. and estimate sums, differences, products, and quotients.
Example: Find the approximate value of 6285 + 13276 + 5217.
- 24900
- 24800
- 24850
- None of these
Solution: (2)
- The approximate value of 6285 is 6300.
- The approximate value of 13276 is 13300.
- The approximate value of 5217 is 5200.
- Therefore, the approximate sum = 6300 + 13300 + 5200 = 24800.
Example: Find the approximate value of 22 × 77.
- 1600
- 1700
- 1650
- None of these
Solution: (1)
- The approximate value of 22 is 20.
- The approximate value of 77 is 80.
- Therefore, the approximate value of 22 × 77 = 20 × 80 = 1600.
Example: Find the approximate thousand of 9876321.
- 9876321
- 9876000
- 987700
- None of these
Solution: (2)
Approximation of 9876321 = 9876000.
Tests for Divisibility
Divisibility by 2
Rule: If the last digit of any number is even or zero, then the number is divisible by 2.
Examples: 12, 86, 130, 568926, and 5983450 are divisible by 2.
Divisibility by 3
Rule: If the sum of the digits of a number is divisible by 3, then the number is also divisible by 3.
Examples: 8349 → 8 + 3 + 4 + 9 = 24 (divisible by 3), hence 8349 is divisible by 3.
Divisibility by 4
Rule: If the last two digits of a number are divisible by 4, then the number is divisible by 4.
Examples: 324, 5632, 3500, 4320, 89412, 84300 are divisible by 4 because their last two digits are divisible by 4.
Divisibility by 5
Rule: If a number ends with 5 or 0, then the number is divisible by 5.
Examples:
(i) 1345 → last digit is 5, so divisible by 5.
(ii) 1340 → last digit is 0, so divisible by 5.
Divisibility by 6
Rule: A number is divisible by 6 if it is divisible by both 2 and 3.
Examples:
(i) 120 → last digit is 0 and sum of digits (1 + 2 + 0 = 3) is divisible by 3, so divisible by 6.
(ii) 1056 → last digit is even (6) and sum of digits (1 + 0 + 5 + 6 = 12) is divisible by 3, so divisible by 6.
Divisibility by 7
Rule: If the difference between twice the unit digit and the number formed by other digits is 0 or a multiple of 7, then the number is divisible by 7.
Example: 581 → 58 - 2*1 = 56 (divisible by 7), hence 581 is divisible by 7.
Divisibility by 8
Rule: If the last three digits of a number are divisible by 8, then the number is also divisible by 8.
Examples:
(i) 3648 → last three digits 648 are divisible by 8, so divisible by 8.
(ii) 2880 → last three digits 880 are divisible by 8, so divisible by 8.
(iii) 216000 → last three digits are 000, so divisible by 8.
Divisibility by 9
Rule: If the sum of all the digits of a number is divisible by 9, then the number is also divisible by 9.
Examples:
(i) 39681 → 3 + 9 + 6 + 8 + 1 = 27 (divisible by 9), hence 39681 is divisible by 9.
(ii) 456138 → 4 + 5 + 6 + 1 + 3 + 8 = 27 (divisible by 9), hence 456138 is divisible by 9.
Divisibility by 10
Rule: Any number ending with zero or more than one zero is divisible by 10.
Examples: 150, 7250, 1900, 35450, etc. are divisible by 10.
Divisibility by 11
Rule: If the difference between the sums of digits at odd and even places is 0 or divisible by 11, then the number is divisible by 11.
Examples:
(i) 3245682 → odd place value sum (3 + 4 + 6 + 2) = 15 and even place value sum (2 + 5 + 8) = 15, so divisible by 11.
(ii) 283712 → odd place value sum (2 + 3 + 1) = 6 and even place value sum (8 + 7 + 2) = 17, differing by 11, so divisible by 11.
V-BODMAS Rule
In order to simplify a numerical expression using various operations like addition, subtraction, multiplication, division, and brackets, a particular sequence of operations must be followed, known by the acronym V-BODMAS:
- V → Vinculum (a horizontal line drawn over a group of numbers or bar ‘−’)
- B → Bracket
- O → of (×)
- D → Division (÷)
- M → Multiplication (×)
- A → Addition (+)
- S → Subtraction (−)
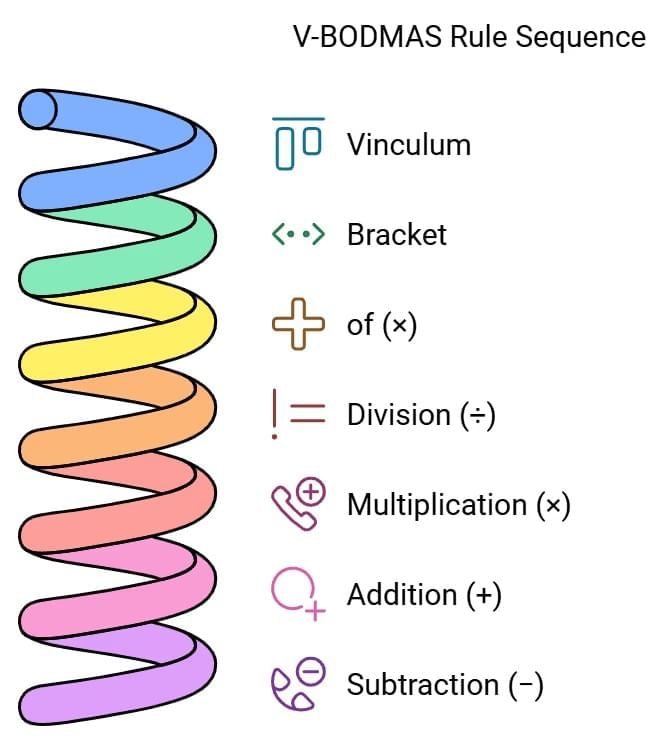
Important notes:
- ‘Of’ means multiplication and is operated before division.
- Order of brackets must be executed in the following order:
- Vi → Vinculum or Bar ‘−’
- Ci → Circular Bracket ()
- Cu → Curly Bracket {}
- Sq → Square Bracket []
Example : 225 ÷ 5 of 3 + 17 − 8 × 12 ÷ 6 is equal to
- 12
- 16
- 14
- 6
Solution: (2)
225 ÷ 5 of 3 + 17 − 8 × 12 ÷ 6
- First, perform multiplication (‘of’): 225 ÷ 15 + 17 − 8 × 12 ÷ 6
- Then, division: 15 + 17 − 8 × 12 ÷ 6
- Multiplication: 15 + 17 − 96 ÷ 6
- Division: 15 + 17 − 16
- Resulting in: 16
Example : If ‘−’ means ‘+’, ‘×’ means ‘−’, ‘÷’ means ‘×’, and ‘+’ means ‘÷’, then find the value of ‘20 − 8 × 3 ÷ 18 + 9’.
- 25
- 24
- 22
- 23
Solution: (3)
20 − 8 × 3 ÷ 18 + 9
- Substituting according to the given replacements: 20 + 8 − 3 × 18 ÷ 9
- Perform multiplication: 20 + 8 − 54 ÷ 9
- Perform division: 20 + 8 − 6
- Resulting in: 22
Important Identities
Some important identities used for simplification are given below:
- (a2 + b2) = (a + b)2 - 2ab
- (a - b)2 = a2 - 2ab + b2
- a2 - b2 = (a + b)(a - b)
- (a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca)
- (a + b)3 = a3 + b3 + 3ab(a + b)
- a3 + b3 = (a + b)(a2 - ab + b2)
- a3 - b3 = (a - b)(a2 + ab + b2)
- (a + b + c)3 = a3 + b3 + c3 + 3(a + b)(b + c)(c + a)
- If a + b + c = 0, then a3 + b3 + c3 = 3abc
- (a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca)
- (a + b + c)3 = a3 + b3 + c3 - 3(a + b)(b + c)(c + a)
Two-digit Number and Arithmetic Series
Every number from 10 to 99 is a two-digit number. The digit on the left is at the tens place and the digit on the right is at the one’s place. To obtain a two-digit number, the digit at the tens place is multiplied by 10 and added to the digit at the one’s place. The sum obtained will be the required two-digit number.
For example, if the digit at the one’s place is 3 and the digit at the tens place is 4, then the required number will be:
4 × 10 + 3 = 40 + 3 = 43
Example:The sum of the digits of a two-digit number is 13. If the digits of this number are reversed, then the new number will be 9 less than the original number. Find the original number.
- 67
- 76
- 72
- 65
Solution: (2)
Let the original number be ( 10x + y ).
Sum of digits: ( x + y = 13 ) …(i)
New number: ( 10y + x )
According to the question:
( 10x + y - (10y + x) = 9 )
( 9x - 9y = 9 )
( x - y = 1 ) …(ii)
Solving equations (i) and (ii):
From Eq. (i), ( x = 7 )
From Eq. (ii), ( y = 6 )
Therefore, the required number is \( 10 \times 7 + 6 = 76 \).
Arithmetic Series of Numbers
Sometimes the difference of two consecutive terms is constant, in which case the series is called an Arithmetic series.
Let the series be ( a, a+d, a+2d, a+3d, ...).
Here, ( a ) is the first term and ( d ) is the common difference.
The ( n )-th term of this series is ( Tn = a + (n-1)d ).
The sum of the first ( n ) terms of this series is 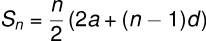
|
82 videos|300 docs|69 tests
|
FAQs on Notes: Number System - Mathematics & Pedagogy Paper 2 for CTET & TET Exams - CTET & State TET
| 1. What is the greatest and lowest number that can be formed with n-digits? |  |
| 2. How are Roman numerals different from the decimal number system? |  |
| 3. What are the different classifications of numbers? |  |
| 4. What are the properties of operations on numbers? |  |
| 5. How do you test for divisibility for numbers? |  |






















