Year 11 Exam > Year 11 Notes > Mathematics for GCSE/IGCSE > Solving Linear Equations
Solving Linear Equations | Mathematics for GCSE/IGCSE - Year 11 PDF Download
What are linear equations?
- A linear equation is an equation that results in a straight line when graphed.
- The highest power in a linear equation is 1, indicating no terms of x2 or higher.
- A standard linear equation takes the form ax + b = c, where a, b, and c are constants, and x is the variable.
How do I solve a linear equation?
- To solve a linear equation, isolate the variable, usually x, by performing inverse operations on both sides of the equation.
- Inverse operations are the opposite of the operations previously applied to the variable.
- The order in which inverse operations are performed is important.
- Generally, this will follow BIDMAS (Brackets, Indices, Division/Multiplication, Addition/Subtraction) in reverse order.
- However, the exact sequence depends on the order in which the original operations were applied to the variable to form the equation.
How do I solve a linear equation of the form ax + b = c?
- The operations that have been applied to x here are:
- STEP 1: Multiply by a
- STEP 2: Add b
- To solve this, you must carry out the inverse operations in reverse order:
- STEP 1: Subtract b
- STEP 2: Divide by a
- For example, to solve the equation 2x + 1 = 9:
- STEP 1: Subtract 1

- STEP 2: Divide by 2

- STEP 1: Subtract 1
- Be extra careful if any of the terms have negatives. For example, to solve the equation 2 − 3x = 10:
- STEP 1: Subtract 2

- STEP 2: Divide by -3 (be careful not to drop the negative sign)

- STEP 1: Subtract 2
How to Solve a Linear Equation with X on Both Sides
- When dealing with a linear equation that has the unknown variable 'x' on both sides, the first step is to gather all terms with 'x' on one side of the equation. This simplifies the process.
- It's usually easier to move the term with the smallest coefficient to the other side. This means shifting the term with the lowest number in front of 'x'.
- For example, to solve the equation 4x − 7 = 11 + x:
- STEP 1: Move the 𝑥 x term with the smallest coefficient of x. The coefficients are 4 and 1, so move the x-term on the right-hand side:

- STEP 2: Solve the linear equation using the method above:
3x - 7 = 11
3x = 18
x = 6
- STEP 1: Move the 𝑥 x term with the smallest coefficient of x. The coefficients are 4 and 1, so move the x-term on the right-hand side:
How do I solve a linear equation that contains brackets?
- If a linear equation contains brackets on one or both sides, start by expanding the brackets.
- For example, to solve the equation 2(x − 1) = 10 − (3 + x):
- STEP 1: Expand the brackets on both sides:
2x − 2 = 10 − 3 − x - STEP 2: Collect the x-terms to one side by subtracting the term with the smaller coefficient of x:
 Be extra careful if any of the terms have negatives
Be extra careful if any of the terms have negatives - STEP 3: Solve the linear equation using the method above:
3x - 2 = 7
3x = 9
x = 3
- STEP 1: Expand the brackets on both sides:
How do I solve a linear equation that contains fractions?
- If a linear equation contains a fraction on one or both sides, remove the fractions by multiplying both sides by everything on the denominator.
- Remember to put brackets around the expression first.
- For example, to solve the equation
 you will need to multiply both sides of the equation by both (x + 3) and (4 - 2x)
you will need to multiply both sides of the equation by both (x + 3) and (4 - 2x) - STEP 1: Multiply both sides by (x + 3)

- STEP 2: Multiply both sides by (4 - 2x)

- STEP 3: Expand the brackets on both sides

- STEP 4: Collect the x terms to one side by subtracting the term with the smaller coefficient of x

- STEP 5: Solve the equation: You can swap the sides if it makes solving the equation easier

The document Solving Linear Equations | Mathematics for GCSE/IGCSE - Year 11 is a part of the Year 11 Course Mathematics for GCSE/IGCSE.
All you need of Year 11 at this link: Year 11
|
84 videos|120 docs
|
FAQs on Solving Linear Equations - Mathematics for GCSE/IGCSE - Year 11
| 1. How do you solve linear equations of the form Ax + B = C? |  |
Ans. To solve linear equations of the form Ax + B = C, you can isolate the variable x by first subtracting B from both sides and then dividing by A. This will give you the value of x.
| 2. What are some techniques to solve linear equations with fractions? |  |
Ans. To solve linear equations with fractions, you can first eliminate the fractions by multiplying both sides of the equation by the least common multiple of the denominators. This will allow you to work with whole numbers and solve the equation more easily.
| 3. How can you solve a linear equation with x on both sides? |  |
Ans. To solve a linear equation with x on both sides, you can first simplify the equation by combining like terms on each side. Then, you can move all terms containing x to one side of the equation and constants to the other side. Finally, solve for x by isolating it on one side of the equation.
| 4. Can you provide steps to solve a linear equation with brackets? |  |
Ans. To solve a linear equation with brackets, you can first distribute the term outside the brackets to each term inside the brackets. Then, simplify the equation by combining like terms. Finally, isolate the variable on one side of the equation by performing inverse operations.
| 5. What are some common mistakes to avoid when solving linear equations? |  |
Ans. Some common mistakes to avoid when solving linear equations include not distributing correctly, forgetting to combine like terms, and making errors in performing inverse operations. It is important to double-check your work and ensure that each step is accurate to arrive at the correct solution.

|
Explore Courses for Year 11 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches



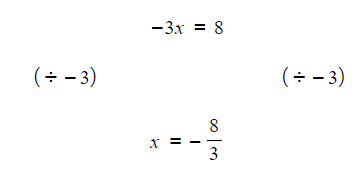

 Be extra careful if any of the terms have negatives
Be extra careful if any of the terms have negatives you will need to multiply both sides of the equation by both (x + 3) and (4 - 2x)
you will need to multiply both sides of the equation by both (x + 3) and (4 - 2x)




















