Applications of Differentiation | Mathematics for GCSE/IGCSE - Year 11 PDF Download

Finding Stationary Points & Turning Points

• A turning point can be thought of as a point where a curve transitions from moving upwards to moving downwards, or vice versa. 
• These points are also referred to as stationary points. "Stationary" denotes that the gradient is zero (flat) at these points.

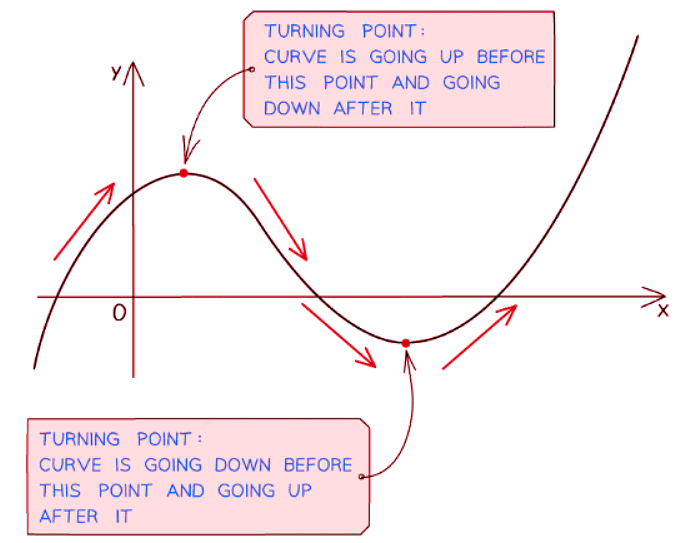
• At a turning point, the gradient of the curve equals zero. 
  • When a tangent is drawn at a turning point, it forms a horizontal line, which inherently has a gradient of zero. 
• Therefore, substituting the x-coordinate of a turning point into the gradient function (also known as the derived function or derivative) will yield an output of zero.

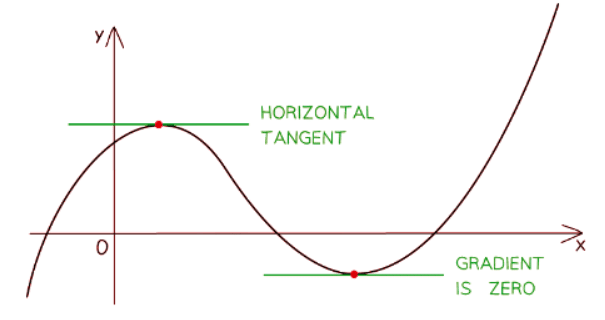
How do I find the coordinates of a turning point?

• STEP 1: Determine the x-coordinate of the turning point by solving the equation of the gradient function (derivative) when it equals zero ie. solve
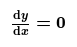
  • x-coordinate: The value of x where the turning point occurs.
• STEP 2: Find the y-coordinate of the turning point by substituting the x-coordinate into the graph's equation, not the gradient function.
  • y-coordinate: The corresponding y-value for the x-coordinate at the turning point.

Classifying Stationary Points

What are the different types of stationary points?

• You can identify different types of stationary points by observing the shape of a curve.
• There are two main types of stationary points, also known as turning points:
  • Maximum points: These points represent peaks on the graph.
  • Minimum points: These points represent troughs on the graph.

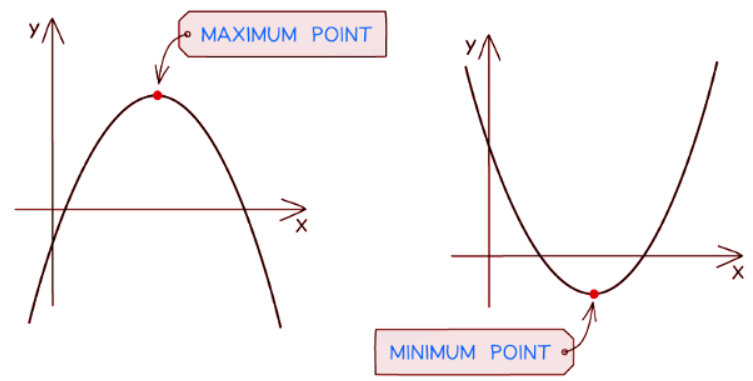
• Local Maximum/Minimum Points: These points are sometimes referred to as local maximum/minimum points because other parts of the graph may reach higher or lower values.

How do I use graphs to classify which is a maximum point and which is a minimum point?

• You can determine whether a point on a curve is a maximum or minimum point by:
  • Observing the shape of the curve, either from a provided sketch or one drawn by yourself.
  • Analyzing the equation of the curve.
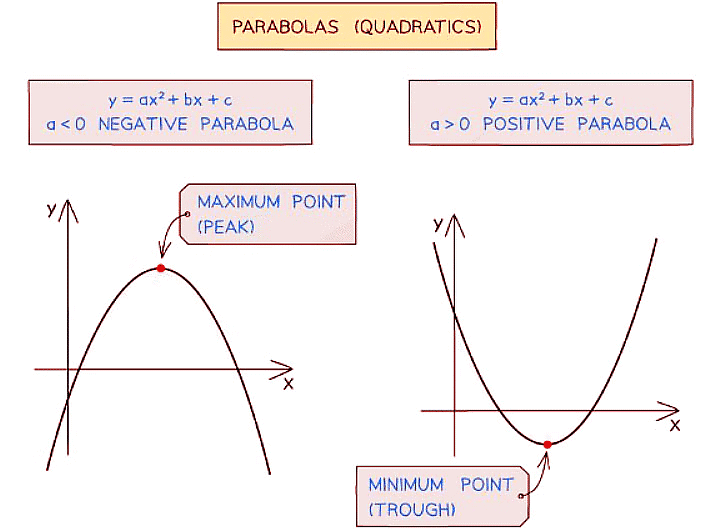
• For parabolas (quadratics), it's straightforward:
  • A positive parabola (with a positive x² term) exhibits a minimum point.
  • A negative parabola (with a negative x² term) displays a maximum point.

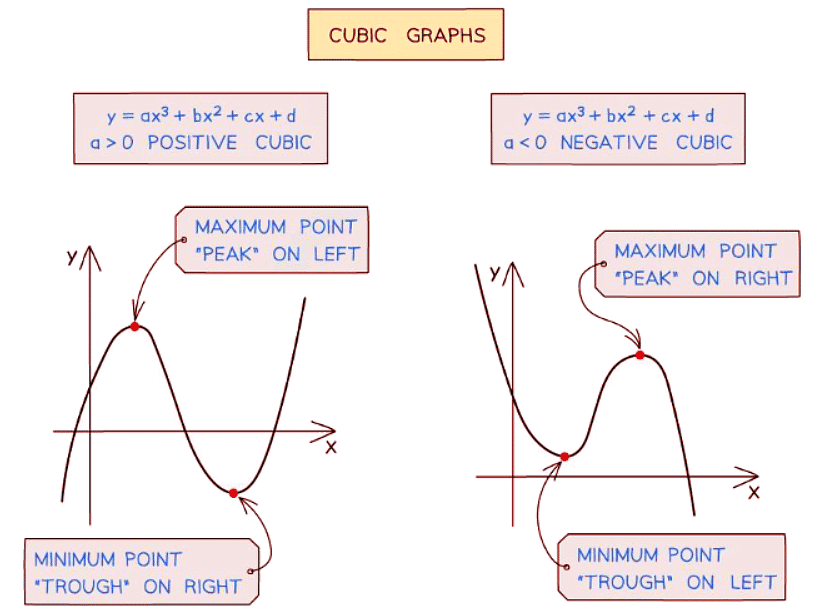
• Cubic graphs are also easily identifiable:
  • A positive cubic graph features a maximum point on the left and a minimum point on the right.
  • Conversely, a negative cubic graph showcases a minimum point on the left and a maximum point on the right.

How do I use the second derivative to classify which is a maximum point and which is a minimum point?

• The second derivative, denoted as 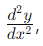represents the derivative of the derivative. To obtain this expression, differentiate the original expression dx/dy twice.
• An algebraic test to find the turning point without sketching involves the following steps:
  • If the stationary point is at x = a, substitute x = a into the expression for 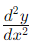 to obtain a numerical value.
  • If this value is negative 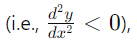 the stationary point is a maximum point.
  • If the value is positive 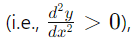 the stationary point is a minimum point.
  • If the value is zero 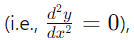 the test is inconclusive, and further analysis or sketching is required to classify the stationary point.
• A zero value could imply a maximum, minimum, or another type of stationary point. Therefore, returning to sketching the graph is necessary for classification.