Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Reflections
Reflections | Mathematics for GCSE/IGCSE - Class 10 PDF Download
What is a reflection?
- Reflection involves creating a mirror image of an object across a line known as the line of reflection or mirror line.
- The reflected image maintains the same shape and size as the original object, but it undergoes a "flip" across the mirror line, resulting in a new position and orientation.
- Points situated on the mirror line remain stationary; they do not change position during the reflection process.
How do I reflect a shape?
- You should be capable of conducting a reflection on a coordinate grid.
- The perpendicular distance between a point on the original object and the mirror line should be equal to the perpendicular distance between the corresponding point on the reflected image and the mirror line.
Key Steps for Shape Reflection:
- Step 1: Measure the perpendicular distance from a point on the original object to the mirror line.
- Step 2: Extend from that point on the mirror line, in the same direction, and measure the same distance again.
- Step 3: Identify and mark the corresponding point on the reflected image at the position you've reached.
- Step 4: Connect the reflected points and label the reflected image accordingly.
1. Vertical lines (of the form x equals k, for some number k):
- The perpendicular distance can be found by counting the number of squares horizontally from a point on the original object until you reach the mirror line
2. Horizontal lines (of the form y equals k, for some number k):
- The perpendicular distance can be found by counting the number of squares vertically from a point on the original object until you reach the mirror line
3. Diagonal lines (of the form y = m x + c, see straight line graphs):
- Reflecting in diagonal lines can be much tricker
- The perpendicular distance can be measured directly using a ruler
- You can also count the number of squares horizontally and vertically until you reach the mirror line, e.g. 2 to the right, 3 down, then from the same point on the mirror line, count the number of squares vertically that was the previous horizontal distance and count the number of squares horizontally that was the previous vertical distance, e.g. 3 to the right, 2 down
4. Double Reflections:
- Double reflections are where the mirror line passes through the shape being reflected
- Part of the shape gets reflected on one side of the mirror line, the other part gets reflected on the other side
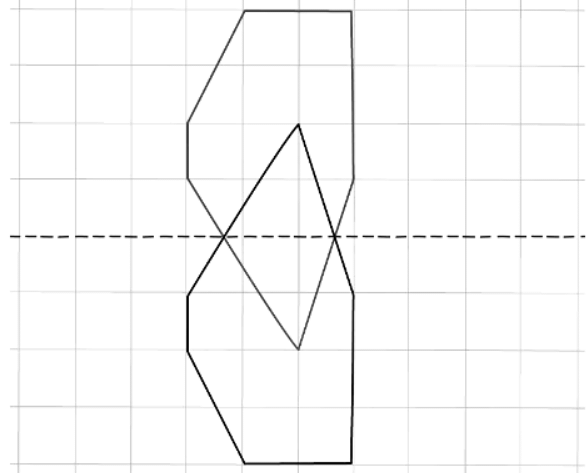 5. Regular polygons:
5. Regular polygons:
- Regular polygons like squares can appear unchanged even after undergoing reflection or other transformations.
- There might be no apparent indication that the shape has been reflected; it might seem like a mere translation.
- However, to identify reflection, one must examine a vertex and its corresponding position. In a reflection, the vertex will appear "back-to-front" on the other side.

How do I describe a reflection?
- To earn full marks, it's crucial to identify and describe a reflection accurately:
- Clearly state that the transformation being discussed is a reflection.
- Provide the mathematical equation that represents the mirror line.
- Ensuring these two components are included in the description is essential for comprehensive understanding and completeness in describing the transformation.
Question for ReflectionsTry yourself: Which of the following describes a reflection?View Solution
The document Reflections | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
66 videos|674 docs|19 tests
|
FAQs on Reflections - Mathematics for GCSE/IGCSE - Class 10
| 1. How can I perform a shape reflection in geometry? |  |
Ans. To perform a shape reflection in geometry, you need to first identify the line of reflection. Then, you can reflect each point of the shape across this line by moving it the same distance on the opposite side of the line.
| 2. What are the different methods of reflection in geometry? |  |
Ans. The different methods of reflection in geometry include reflecting in vertical lines, horizontal lines, and diagonal lines. Each method involves reflecting the shape across a specific axis or line.
| 3. How can I reflect a shape in a diagonal line? |  |
Ans. To reflect a shape in a diagonal line, you can follow the same process as reflecting in a vertical or horizontal line. However, make sure to adjust the position of the points based on the diagonal line's orientation.
| 4. How do reflections apply to regular polygons in geometry? |  |
Ans. Reflections can be used to create symmetrical shapes with regular polygons. By reflecting a regular polygon across a line of symmetry, you can create a mirror image of the original shape.
| 5. What are some key concepts to understand about reflections in geometry? |  |
Ans. Some key concepts to understand about reflections in geometry include the line of reflection, the distance of each point from the line, and how reflections can create symmetry in shapes. Understanding these concepts is essential for mastering reflection techniques in geometry.
Related Searches















