Notes: Division | Mathematics & Pedagogy Paper 1 for CTET & TET Exams - CTET & State TET PDF Download
Division is a fundamental arithmetic operation essential for developing numerical proficiency. It is a crucial topic in the Central Teacher Eligibility Test (CTET) and state-level Teacher Eligibility Tests (TETs). Understanding division helps students solve problems related to equal distribution and partitioning.
Division is the process of distributing a number into equal parts. For example, dividing 12 by 3 (12 ÷ 3) means splitting 12 into 3 equal parts, resulting in 4.
Meaning of Division
Let's say you have 10 cookies, and you want to share them equally among 5 friends.
To do division, you'll need to divide the total number of cookies (10) by the number of friends (5).
So, 10 ÷ 5 = 2.
This means each friend will get 2 cookies.
So, when you divide 10 cookies equally among 5 friends, each friend gets 2 cookies.
Division helps us figure out how to distribute things equally among a group!
Division means equal sharing or equal grouping.
- Suppose, 12 mangoes are shared by 3 boys equally. How many mangoes will each boy get?
 Clearly, each boy will get 4 mangoes.
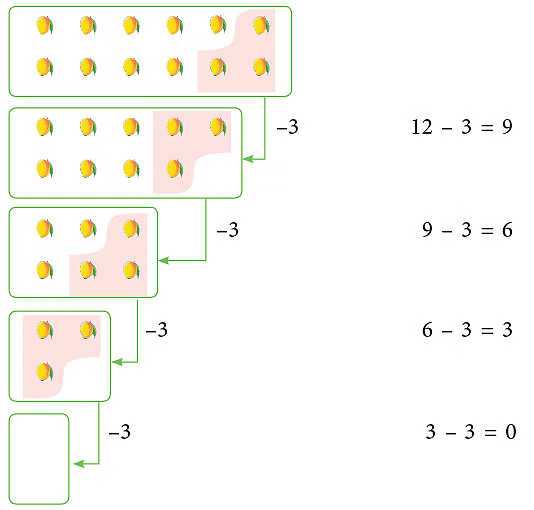
Clearly, each boy will get 4 mangoes. - You can also find the answer by subtraction. Subtract 3 at a time until there are none left.
EduRev Tips: Division and multiplication are inverse operations.
For example: if 42 ÷ 7 = 6 then 7 × 6 = 42.
- How many 3s have been taken away when you reach 0?

- How many times has a group of 3 been removed till finally no mango remains?

- Clearly, 3 has to be subtracted 4 times from 12 to obtain 0 as the final result. So 12 ÷ 4 = 3. You may ask this question as:
 × 3 = 12 or 12 ÷ 4 =
× 3 = 12 or 12 ÷ 4 = From the above explanation, we can say that, division is repeated subtraction.
From the above explanation, we can say that, division is repeated subtraction.
Terms Related to Division
Dividend: The number to be divided is called the dividend.
Divisor: The number by which we divide is called the divisor.
Quotient: The result obtained on division is called the quotient.
Remainder: The number which is left undivided is called the remainder.
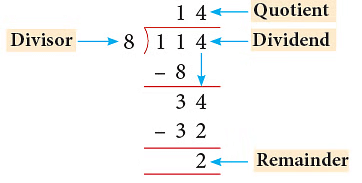
Look at the example above:
1. Verifying Division
To check a division result, multiply the quotient by the divisor and add the remainder to this product. The result should be equal to the dividend. Thus,
(Divisor × Quotient) + Remainder = Dividend
From the above division fact, we have,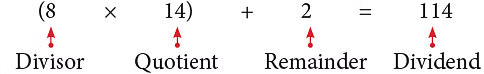 So, our answer is correct.
So, our answer is correct.
2. Some Important Points Related to Division
We always start division from the place of highest value. In case of 2-digit dividends, we start from tens place and in case of 3-digit dividend, we always start from hundreds place. The remainder is always smaller than the divisor.
3. Properties of Division
(i) When any number is divided by 1, the quotient is the number itself.
Examples: 62 ÷ 1 = 62, 125 ÷ 1 = 125
(ii) When any number is divided by itself (except 0), the quotient is 1.
Examples: 64 ÷ 64 = 1, 586 ÷ 586 = 1.
(iii) When 0 is divided by any number (except 0), the quotient is always 0.
Examples: 0 ÷ 58 = 0, 0 ÷ 6423 = 0.
(iv) Division by zero is not allowed.
Division of a Number by a 1-Digit Number
Example 1: Divide 649 by 7.
We divide, as shown alongside.
- Start by looking at the first number in the dividend.
- Find a number in the table of 7 less than or equal to 64.
- So, 9 is the required number.7 x 9 = 63 , so write 63 below 64.
- Subtract, the number you got by multiplying the divisor,from the number in the dividend.
- 64 minus 63 equals 1. Bring down the next digit, from the number in the dividend.
- Repeat the same process again.
- 7 x 2 equals 14.So use 7.
- Then, subtract. We get 5 left. This 5 is our remainder.
- And the quotient is 92
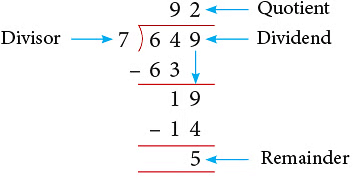 Thus, 649 ÷ 7 gives Q = 92 and R = 5.
Thus, 649 ÷ 7 gives Q = 92 and R = 5.
Check:
Divisor × Quotient + Remainder
= 7 × 92 + 5 = 644 + 5 = 649
Dividing 4-Digit and 5-Digit Numbers by a 1- Digit Number
Example 2: Divide 4589 by 6.
Solution:
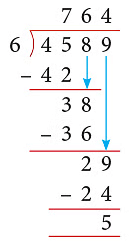
- First, consider the thousands place. The divisor 6 does not divide into the first figure 4 of the dividend, as 6 > 4, so consider the first two digits 45 of the dividend. 6 goes into 45, 7 times and yields 3 as remainder.
- Write the quotient 7 above 5 in 45. Then, complete as shown by bringing down the digit 8 and lastly the digit 9 of the dividend.
Check: To check answer, we use the relationship,
Dividend = Divisor × Quotient + Remainder
- Here, Divisor = 6, Quotient = 764, Remainder = 5 and Dividend = 4589.
So, Dividend = Divisor × Quotient + Remainder.
= 6 × 764 + 5 = 4584 + 5 = 4589 - Thus, 4589 ÷ 6 gives Q = 764 and R = 5.
Example 3: Divide 7982 by 7.
Solution:
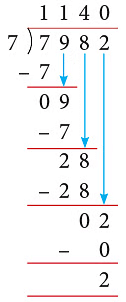
Thus, 7982 ÷ 7 gives Q = 1140 and R = 2.
Example 4: Divide 67316 by 7.
Solution:
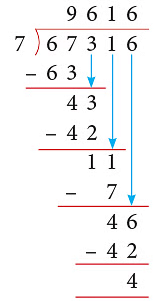
Thus, 67316 ÷ 7 gives Q = 9616 and R = 4.
EduRev Tip: 7 does not go into 2 so, we put a 0 in the quotient and bring down 2.
Division of a Number by a 2-Digit Number
Example 5: Divide 5975 by 14.
Solution:

- Starting from the leftmost digits, we consider 59, the number formed by the first two digits 5 and 9 of the dividend, as divisor is a 2-digit number. 14 < 59.
- Using the multiplication table of 14, we see that 14 goes into 59, 4 times and yields 3 as a remainder. Write the quotient 4 above 9 of 59.
- Then, complete the division as shown by bringing down 7 and lastly the figure 5 of the dividend.
Check: Dividend = Divisor × Quotient + Remainder
= 14 × 426 + 11
= 5964 + 11 = 5975 - Thus, 5975 ÷ 14 gives Q = 426 and R = 11.
Example 6: Divide 92682 by 21 and check your answer.
Solution:
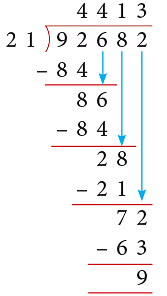
Thus, 92682 ÷ 21 gives Q = 4413 and R = 9.
Check:
Here, divisor = 21, quotient = 4413, remainder = 9 and dividend = 92682.
We have,
Dividend = Divisor × Quotient + Remainder
= 21 × 4413 + 9
= 92673 + 9 = 92682
So, the answer is correct.
Division of a Number by 10, 100 and 1000
Example 7: Divide each of the following numbers by 10.
(a) 58
(b) 723
(c) 8165
Solution:
(a)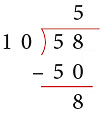 Thus, 58 ÷ 10 gives Q = 5 and R = 8.
Thus, 58 ÷ 10 gives Q = 5 and R = 8.
(b)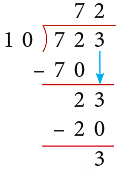
Thus, 723 ÷ 10 gives Q = 72 and R = 3.
(c)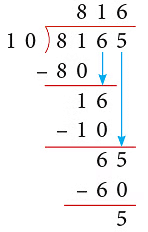 Thus, 8165 ÷ 10 gives Q = 816 and R = 5.
Thus, 8165 ÷ 10 gives Q = 816 and R = 5.
From the above examples, we get the following rule:
Rule: On dividing a number by 10, we remove the digit at the ones place leaving the rest of the digits to form the quotient and the digit we remove from the ones place is the remainder.
Thus,
Example 8: Divide each of the following numbers by 100.
(a) 563
(b) 7289
(c) 17019
Solution:
(a)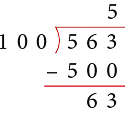 Thus, 563 ÷ 100 gives Q = 5 and R = 63.
Thus, 563 ÷ 100 gives Q = 5 and R = 63.
(b)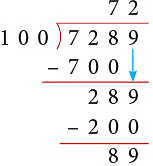 Thus, 7289 ÷ 100 gives Q = 72 and R = 89.
Thus, 7289 ÷ 100 gives Q = 72 and R = 89.
(c)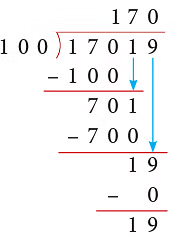 Thus, 17019 ÷ 100 gives Q = 170 and R = 19.
Thus, 17019 ÷ 100 gives Q = 170 and R = 19.
From the above examples, we get the following rule:
Rule: On dividing a number by 100, we remove the digits at the ones and tens places leaving the rest of the digits to form the quotient and the digits we remove from the ones and tens places form the remainder.
Thus,
Example 9: Divide each of the following numbers by 1000.
(a) 5637
(b) 15863
(c) 743895
Solution:
(a)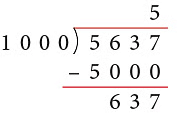 Thus, 5637 ÷ 1000 gives Q = 5 and R = 637.
Thus, 5637 ÷ 1000 gives Q = 5 and R = 637.
(b)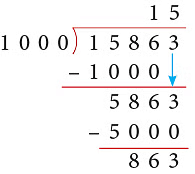 Thus, 15863 ÷ 1000 gives Q = 15 and R = 863.
Thus, 15863 ÷ 1000 gives Q = 15 and R = 863.
(c)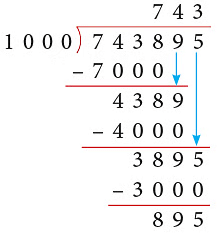 Thus, 743895 ÷ 1000 gives Q = 743 and R = 895.
Thus, 743895 ÷ 1000 gives Q = 743 and R = 895.
From the above examples, we get the following rule:
Rule: On dividing a number by 1000, we remove the digits at the ones, tens and hundreds places to get the remainder and the rest of the digits form the quotient.
Thus,
Division of a Number by Multiples of 10 and 100
Example 10: Divide 6832 by 50.
Solution:
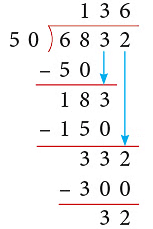 Thus, 6832 ÷ 50 gives Q = 136 and R = 32.
Thus, 6832 ÷ 50 gives Q = 136 and R = 32.
Example 11: Divide 52891 by 600.
Solution:
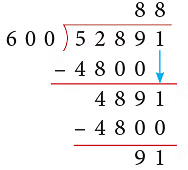 Thus, 52891 ÷ 600 gives Q = 88 and R = 91.
Thus, 52891 ÷ 600 gives Q = 88 and R = 91.
Problems Based on Real Life Situations
When you do a division problem, sometimes the remainder forms the part of your answer and sometimes it doesn’t.
Some Solved Examples
Example 12: 996 students of a school went on a picnic. They boarded buses each of which could hold only 24 students. How many buses were required?
Solution:
- At first, we divide 996 by 24 as shown on the right.
- If we use the quotient 41 as the number of buses needed, then 12 students cannot go for the picnic.
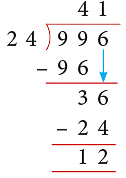 So, we need to have one more bus to answer the question correctly.
So, we need to have one more bus to answer the question correctly.
Thus, 42 buses were needed to take the students for the picnic.
Example 13: The sports teacher is cutting ribbons for the sports medals. How many ribbons of 30 cm length can the teacher get from a roll of ribbon that is 1520 cm long?
Solution:
At first, we divide 1520 by 30.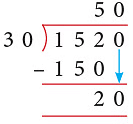
- Here, we ignore the remainder as the question asks for the number of pieces exactly 30 cm in length.
Thus, the teacher will get 50 pieces each of 30 cm length.
Example 14: Five friends together purchased a cricket kit for ₹ 7925. Find the money contributed by each child.
Solution:
- Money contributed by 5 children = ₹ 7925
- Money contributed by 1 child = ₹ 7925 ÷ 5
= ₹ 1585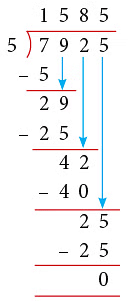
Thus, the money contributed by each child is ₹ 1585.
Example 15: The product of two numbers is 22120. If one of the numbers is 35, find the other number.
Solution:
- Product of two numbers = 22120
- One of the numbers = 35
- So, the other number = Product ÷ Given number
= 22120 ÷ 35 = 632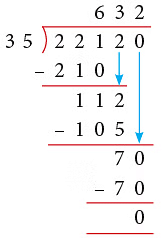
Thus, the other number is 632.
|
30 videos|210 docs|69 tests
|
FAQs on Notes: Division - Mathematics & Pedagogy Paper 1 for CTET & TET Exams - CTET & State TET
| 1. How can division be defined in mathematics? |  |
| 2. What are some terms related to division? |  |
| 3. How do you divide a number by a 1-digit number? |  |
| 4. How do you divide a number by a 2-digit number? |  |
| 5. How can division of a number by multiples of 10 and 100 be done? |  |
















