Mastering Development in Python: Assignment 2 | Python- Mastering Development in Python - Software Development PDF Download
Q1: Balanced strings are those that have an equal quantity of 'L' and 'R' characters.
Given a balanced string s, split it into some number of substrings such that:
Each substring is balanced.
Return the maximum number of balanced strings you can obtain.
Example 1:
Input: s = "RLRRLLRLRL"
Output: 4
Explanation: s can be split into "RL", "RRLL", "RL", "RL", each substring contains same number of 'L' and 'R'.
Example 2:
Input: s = "RLRRRLLRLL"
Output: 2
Explanation: s can be split into "RL", "RRRLLRLL", each substring contains same number of 'L' and 'R'.
Note that s cannot be split into "RL", "RR", "RL", "LR", "LL", because the 2nd and 5th substrings are not balanced.
Example 3:
Input: s = "LLLLRRRR"
Output: 1
Explanation: s can be split into "LLLLRRRR".
Constraints:
2 <= s.length <= 1000
s[i] is either 'L' or 'R'.
s is a balanced string.
Ans: 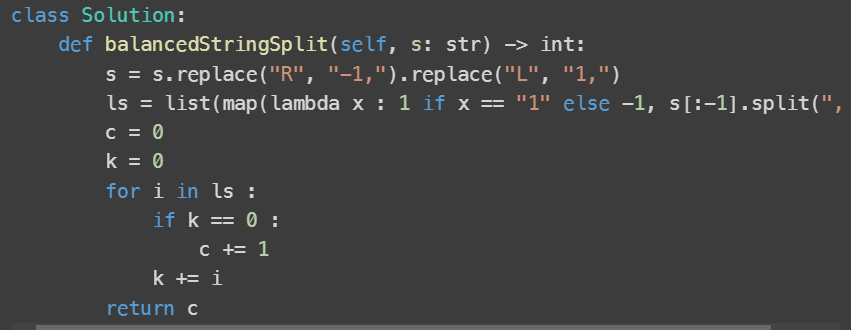
Q2: You are given a positive integer num consisting of exactly four digits. Split num into two new integers new1 and new2 by using the digits found in num. Leading zeros are allowed in new1 and new2, and all the digits found in num must be used.
For example, given num = 2932, you have the following digits: two 2's, one 9 and one 3. Some of the possible pairs [new1, new2] are [22, 93], [23, 92], [223, 9] and [2, 329].
Return the minimum possible sum of new1 and new2.
Example 1:
Input: num = 2932
Output: 52
Explanation: Some possible pairs [new1, new2] are [29, 23], [223, 9], etc.
The minimum sum can be obtained by the pair [29, 23]: 29 + 23 = 52.
Example 2:
Input: num = 4009
Output: 13
Explanation: Some possible pairs [new1, new2] are [0, 49], [490, 0], etc.
The minimum sum can be obtained by the pair [4, 9]: 4 + 9 = 13.
Constraints:
1000 <= num <= 9999
Ans: 
Q3: You are given a positive integer num consisting only of digits 6 and 9.
Return the maximum number you can get by changing at most one digit (6 becomes 9, and 9 becomes 6).
Example 1:
Input: num = 9669
Output: 9969
Explanation:
Changing the first digit results in 6669.
Changing the second digit results in 9969.
Changing the third digit results in 9699.
Changing the fourth digit results in 9666.
The maximum number is 9969.
Example 2:
Input: num = 9996
Output: 9999
Explanation: Changing the last digit 6 to 9 results in the maximum number.
Example 3:
Input: num = 9999
Output: 9999
Explanation: It is better not to apply any change.
Constraints:
1 <= num <= 104
num consists of only 6 and 9 digits.
Ans: Code

Q4: You are given a 0-indexed integer array nums and an integer k. Your task is to perform the following operation exactly k times in order to maximize your score:
Select an element m from nums.
Remove the selected element m from the array.
Add a new element with a value of m + 1 to the array.
Increase your score by m.
Return the maximum score you can achieve after performing the operation exactly k times.
Example 1:
Input: nums = [1,2,3,4,5], k = 3
Output: 18
Explanation: We need to choose exactly 3 elements from nums to maximize the sum.
For the first iteration, we choose 5. Then sum is 5 and nums = [1,2,3,4,6]
For the second iteration, we choose 6. Then sum is 5 + 6 and nums = [1,2,3,4,7]
For the third iteration, we choose 7. Then sum is 5 + 6 + 7 = 18 and nums = [1,2,3,4,8]
So, we will return 18.
It can be proven, that 18 is the maximum answer that we can achieve.
Example 2:
Input: nums = [5,5,5], k = 2
Output: 11
Explanation: We need to choose exactly 2 elements from nums to maximize the sum.
For the first iteration, we choose 5. Then sum is 5 and nums = [5,5,6]
For the second iteration, we choose 6. Then sum is 5 + 6 = 11 and nums = [5,5,7]
So, we will return 11.
It can be proven, that 11 is the maximum answer that we can achieve.
Constraints:
1 <= nums.length <= 100
1 <= nums[i] <= 100
1 <= k <= 100
Code: 
Q5: You are given an integer array nums (0-indexed). In one operation, you can choose an element of the array and increment it by 1.
For example, if nums = [1,2,3], you can choose to increment nums[1] to make nums = [1,3,3].
Return the minimum number of operations needed to make nums strictly increasing.
An array nums is strictly increasing if nums[i] < nums[i+1] for all 0 <= i < nums.length - 1. An array of length 1 is trivially strictly increasing.
Example 1:
Input: nums = [1,1,1]
Output: 3
Explanation: You can do the following operations:
1) Increment nums[2], so nums becomes [1,1,2].
2) Increment nums[1], so nums becomes [1,2,2].
3) Increment nums[2], so nums becomes [1,2,3].
Example 2:
Input: nums = [1,5,2,4,1]
Output: 14
Example 3:
Input: nums = [8]
Output: 0
Constraints:
1 <= nums.length <= 5000
1 <= nums[i] <= 104
Code: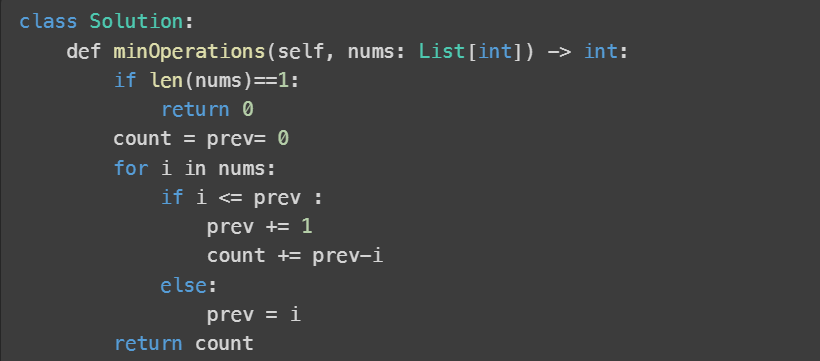
|
8 videos|5 docs
|
FAQs on Mastering Development in Python: Assignment 2 - Python- Mastering Development in Python - Software Development
| 1. পরীক্ষায় কি ধরণের প্রশ্ন থাকবে? |  |
| 2. পরীক্ষায় কি সময়কাল থাকবে? |  |
| 3. কি ধরনের স্থানে পরীক্ষা হবে? |  |
| 4. পরীক্ষায় কি ধরণের প্রশ্ন থাকবে, বিষয়টি নিয়ে চিন্তিত থাকবো? |  |
| 5. পরীক্ষায় কি ধরণের পাস মার্ক থাকবে? |  |





















