MCQs with Solutions: Quadrilaterals - 1 | Mathematics (Maths) Class 9 PDF Download
Q1: The length of each side of a rhombus is 10cm and one of its diagonal is of length 16cm. The Length of the other Diagonal is:
(a) 5cm
(b) 12cm
(c) 13cm
(d) 6cm
Ans: b
Sol: Firstly we know that diagonal of rhombus bisects each other. thus half of diagonal =8cm.
by pythagoras theorem we find another half of diagonal.that is 6 cm
as we diagonals bisect other thus another diagonal
=2×6=12cm
Q2: In a Quadrilateral ABCD, AB = BC and CD = DA, then the quadrilateral is a
(a) Triangle
(b) Kite
(c) Rhombus
(d) Rectangle
Ans: b
Q3: ABCD is a Parallelogram in which AB = 9.5cm and its perimeter is 30cm. Find the length of each side of the Parallelogram?
(a) 9.5cm, 9.5cm, 5.6cm, 5.4cm
(b) 9.5cm, 9.5cm, 5.4cm, 5.6cm
(c) 9.5cm, 9.5cm, 5.5cm, 5.5cm
(d) 10cm, 10cm, 11cm, 11cm
Ans: c
Sol: We know that the perimeter of parallelogram ABCD can be written as
Perimeter = AB + BC + CD + DA
We know that opposite sides of parallelogram are equal
AB = CD and BC = DA
By substituting the values
Perimeter = 9.5 + BC + 9.5 + BC
It is given that perimeter = 30 cm
So we get
30 = 19 + 2BC
It can be written as
2BC = 30 – 19
By subtraction
2BC = 11
By division we get
BC = 5.5 cm
Therefore, AB = 9.5 cm, BC = 5.5 cm, CD = 9.5 cm and DA = 5.5 cm.
Q4: The angle between two altitudes of a Parallelogram through the vertex of an obtuse angle of the Parallelogram of 60∘. Find the angles of the Parallelogram
(a) 150∘, 150∘, 30∘, 30∘
(b) 110∘, 50∘, 105∘, 105∘
(c) 120∘, 60∘, 120∘, 60∘
(d) 200∘, 100∘, 30∘, 30∘
Ans: c
Sol: 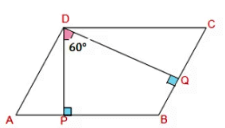
Given ABCD is a parallelogram in which DP ⊥ AB and AQ ⊥ BC.
Given ∠PDQ = 60°
In quadrilateral DPBQ, by the angle sum property, we have:
∠PDQ + ∠DPB + ∠B + ∠BQD = 360°
60° + 90° + ∠B + 90° = 360°
∠B = 360° - 240°
Therefore, ∠B = 120°
But ∠B = ∠D = 120° (Since opposite angles of a parallelogram are equal)
From the figure, we have AB ∥ CD (Since opposite sides of a parallelogram are parallel)
∠B + ∠C = 180° (Since the sum of adjacent interior angles is 180°)
120° + ∠C = 180°
∠C = 180° - 120° = 60°
Therefore, ∠A = ∠C = 60° (Opposite angles of a parallelogram are equal)
Q5: If an angle of a parallelogram is two-third of its adjacent angle, then find the smallest angle of the parallelogram.
(a) 36
(b) 120
(c) 72
(d) 90
Ans: c
Sol:
Let an angle of a parallelogram be x°.
Hence, its adjacent angle = (2/3) × x°
x + (2/3) × x = 180° [∵ Adjacent angles of a parallelogram are supplementary]
⇒ (5/3) x = 180°
x = (180 × 3) / 5 = 108°
∴ Adjacent angle = (2/3) × 108° = 72°
Hence, the smallest angle = 72°
Q6: If ABCD is a Parallelogram with 2 Adjacent angles ∠A =∠B, then the parallelogram is a
(a) Rhombus
(b) Triangle
(c) Rectangle
(d) Square
Ans: c
Q7: Given a triangular prism, then what can we conclude about the lateral faces?
(a) Faces are rectangle
(b) Faces are Trapezium
(c) Faces are Prism
(d) both rectangles Faces are Parallelogram
Ans: d
Sol: In a triangular prism, the bases are triangles and the lateral faces are parallelograms.
Thus it can be both rectangles and parallelograms.
So, option (D) is correct.
If the faces are rectangles, then we call it as right triangular prism
Observe the following figure.
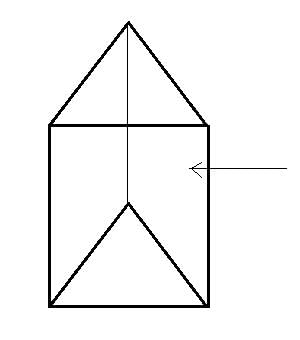
It is clear that the faces of the above figure are rectangles and hence it is right triangular prism.
Q8: If angles A, B, C and D of the quadrilateral ABCD, taken in order, are in the ratio 3:7:6:4, then ABCD is
(a) rhombus
(b) parallelogram
(c) trapezium
(d) kite
Ans: c
Sol: Given, ratio of angles of quadrilateral ABCD is 3 : 7 : 6 : 4.
Let angles of quadrilateral ABCD be 3x, 7x, 6x and 4x, respectively. We know that, sum of all angles of a quadrilateral is 360°.
3x + 7x + 6x + 4x = 360°
=> 20x = 360°
=> x=360°/20° = 18°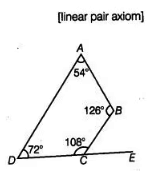 ∠A = 3 × 18 = 54°∠B = 7 × 18 = 126°
∠A = 3 × 18 = 54°∠B = 7 × 18 = 126°
∠C = 6 × 18 = 108°
∠D = 4 × 18 = 72°
From the figure,
∠BCE = 180° - ∠BCD
∠BCE = 180° - 108° = 72°
Here, ∠BCE = ∠ADC = 72°
Since the corresponding angles are equal,
BC ∥ AD
Now, sum of co-interior angles,
∠A + ∠B = 126° + 54° = 180°
∠C + ∠D = 108° + 72° = 180°
Hence, ABCD is a trapezium.
Q9: ABCD is a Trapezium in which AB∥DC and ∠A = ∠B = 45∘. Find angles C and D of the Trapezium
(a) 120∘, 120∘
(b) 135∘, 135∘
(c) 200∘, 50∘
(d) 150∘, 150∘
Ans: b
Q10: Angles of a quadrilateral are in the ratio 3 : 6 : 8: 13. The largest angle is :
(a) 178°
(b) 156°
(c) 90°
(d) 36°
Ans: b
Sol: 3p + 6p + 8p + 13p = 30p = 360° ⇒ p
= 12° Largest angle is 13p = 13 × 12°
= 156°
Q11: If an angle of a parallelogram is two-third of its adjacent angle, the smallest angle of the parallelogram is:
(a) 81∘
(b) 54∘
(c) 108∘
(d) 72∘
Ans: d
Q12: Consecutive angles of a Parallelogram are
(a) Supplementary
(b) Acute
(c) Complementary
(d) Equal
Ans: a
Q13: The angles of a quadrilateral are in the ratio 4: 5: 10: 11. The angles are
(a) 36°, 60°, 108°, 156°
(b) 52°, 60°, 122°, 126°
(c) 48°, 60°, 120°, 132°
(d) 60°, 60°, 120°, 120°
Ans: c
Sol: Let x be the common angle among all the four angles of a quadrilateral.
As per angle sum property, we know:
4x+5x+10x+11x = 360°
30x = 360°
x = 12°
Hence, angles are
4x = 4 (12) = 48°
5x = 5 (12) = 60°
10x = 10 (12) = 120°
11x = 11 (12) = 132°
Q14: One Angle of a quadrilateral is of 108∘ and the remaining three angles are equal. Find each of the three equal angles.
(a) 84∘, 84∘, 84∘
(b) 90∘, 84∘, 90∘
(c) 90∘, 90∘, 84∘
(d) 84∘, 90∘, 90∘
Ans: a
Sol:
Let ABCD be a quadrilateral such that ∠A = 108° and ∠B = ∠C = ∠D
Let ∠B = ∠C = ∠D = x°
Now, by the angle sum property, we have:
∠A + ∠B + ∠C + ∠D = 360°
108° + 3x = 360°
3x = 360° - 108°
x = 252° / 3
x = 84°
Hence, the measure of each of the angles is 84°.
Q15: ABCD is a Rectangle. Find the values of x and y?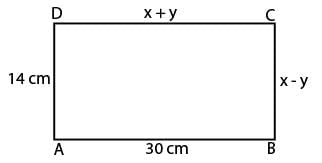
AB =30 DA= 14 DC= x+y CB=x-y
(a) 20 and 10
(b) 25 and 5
(c) 24 and 6
(d) 22 and 8
Ans: d
Sol: ABCD is a rectangle.
∴ AB = CD
⇒ 30 = x + y
or x + y = 30 ..... (i)
Similarly, AD = BC
⇒ 14 = x - y
or x - y = 14 .......(ii)
On adding eq. (i) and (ii), we get
2x = 44
⇒ x = 22
Putting the value of x in eq. (i), we get
22 + y = 30
⇒ y = 30 -22
⇒ y = 8
So, x = 22, y = 8.
Q16: If area of a Parallelogram with sides ‘a’ and ‘b’ is A and that of a rectangle with sides ‘a’ and ‘b’ is B, then
(a) A < B
(b) A = B
(c) A > B
(d) None of these
Ans: a
Q17: A diagonal of a Rectangle is inclines to one side of the rectangle at an angle of 25∘. The Acute Angle between the diagonals is
(a) 115∘
(b) 50∘
(c) 40∘
(d) 25∘
Ans: b
Q18: Diagonals of a Parallelogram ABCD intersect at O. If ∠BOC = 90∘, ∠BDC = 50∘ then ∠OAB is
(a) 10∘
(b) 50∘
(c) 40∘
(d) 90∘
Ans: c
Q19: Angles of a quadrilateral are in the ratio 3 : 4 : 4 : 7. Find all the angles of the quadrilateral.
(a) 60∘, 120∘, 80∘, 140∘
(b) 60∘, 80∘, 100∘, 90∘
(c) 70∘, 70∘, 100∘, 100∘
(d) 60∘, 80∘, 80∘, 140∘
Ans: d
Q20: In Triangle ABC which is right angled at B. Given that AB = 9cm, AC = 15cm and D, E are the mid-points of the sides AB and AC res. Find the length of BC?
(a) 12cm
(b) 13.5cm
(c) 13cm
(d) 15cm
Ans: a
Q21: The Parallel sides of a trapezium are ‘a’ and ‘b’ res. The line joining the mid-points of its non-parallel sides will be
(a) 1/2 (a+b)
(b) 2ab/(a+b)
(c) 1/2 (a-b)
(d) None of These
Ans: a
Q22: If a diagonal AC and BD of a quadrilateral ABCD bisect each other, then ABCD is a
(a) Rectangle
(b) Triangle
(c) Rhombus
(d) Parallelogram
Ans: d
Q23: Which of the following is not true for the Parallelogram?
(a) Opposite angles are bisected by the diagonals
(b) Opposite sides are equal
(c) Opposite angles are equal
(d) Diagonals bisect each other
Ans: a
Q24: The angles of the quadrilateral are in the ratios 3 : 5 : 9 : 13. Find all the angles of the Quadrilateral
(a) 36∘, 60∘, 108∘, 156∘
(b) 36∘, 60∘, 108∘, 154∘
(c) 40∘, 50∘, 80∘, 150∘
(d) 100∘, 60∘, 36∘, 156∘
Ans: a
Q25: The length of each side of a rhombus is 10cm and one of its diagonal is of length 16cm. The Length of the other Diagonal is
(a) 12cm
(b) 6cm
(c) 5cm
(d) 13cm
Ans: a
Sol: Use pythagoras theorem in right triangle,
102 -[16/2]2 = 100 -64 = 36 = [6]2 ; hence the other diagonal = 6x2 = 12cm
|
40 videos|471 docs|57 tests
|
FAQs on MCQs with Solutions: Quadrilaterals - 1 - Mathematics (Maths) Class 9
| 1. What are the properties of a quadrilateral? |  |
| 2. How many types of quadrilaterals are there? |  |
| 3. What is the sum of the interior angles of a quadrilateral? |  |
| 4. How do you determine if a quadrilateral is a parallelogram? |  |
| 5. Can a quadrilateral have all sides of different lengths? |  |





















