Ratio and Proportion | Year 9 Mathematics (Cambridge) PDF Download
Understanding Ratios
A ratio is a way to compare two quantities by showing the relative sizes of two or more values. It tells us how much of one thing there is compared to another.
Examples
Example 1: If there are 2 apples and 3 oranges, the ratio of apples to oranges is 2:3.
Example 2: In a class, if there are 12 boys and 18 girls, the ratio of boys to girls is 12:18. This ratio can be simplified by dividing both numbers by their greatest common divisor (6 in this case), so the simplified ratio is 2:3.
Ratios can also be written in fraction form. For example, the ratio 2:3 can be written as 2/3.
Solving Problems with Ratios
When solving problems with ratios, it's important to understand how to use and manipulate them.
Here are a few key steps:
- Identify the Ratio: Determine what the ratio is comparing.
- Set Up Proportions: Use the given ratio to set up proportions to solve for unknown values.
- Solve the Equation: Use algebraic methods to find the unknown values.
Examples
Example 1: If a recipe calls for 2 cups of flour to 3 cups of sugar and you want to make a half batch, how much of each ingredient would you need?
Sol: Original ratio of flour to sugar: 2 : 3
Half batch:
Flour: 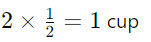
Sugar: 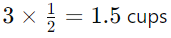
Example 2: If 4 pencils cost $6, how much would 10 pencils cost?
Sol: First, find the cost per pencil by dividing the total cost by the number of pencils:
Cost per pencil = 6/4 = 1.5 dollars
Then, multiply the cost per pencil by the number of pencils you want to find the total cost:
Total cost for 10 pencils = 1.5 × 10 = 15 dollars
Proportional Reasoning
Proportional reasoning involves recognizing and using the multiplicative relationship between ratios. It helps in solving problems that involve proportional relationships, such as scaling recipes, converting units, or working with maps and models.
Examples
Example 1: A map uses a scale of 1 cm to 5 km. If the distance between two cities on the map is 8 cm, what is the actual distance?
Sol: The scale ratio is 1 cm : 5 km. So, multiply the map distance by the scale factor:
Actual distance = 8 cm × 5 km/cm = 40 km
Example 2: If a car travels 300 miles on 10 gallons of gas, how far can it travel on 15 gallons?
Sol: First, find the distance per gallon by dividing the total distance by the number of gallons:
Distance per gallon = 300/10 = 30 miles per gallon
Then, multiply the distance per gallon by the number of gallons to find the total distance:
Total distance = 30 × 15 = 450 miles
Key Points
- Ratios are used to compare quantities.
- Ratios can be simplified by dividing both terms by their greatest common divisor.
- Proportions can be set up and solved using algebra.
- Proportional reasoning helps in solving real-world problems involving scaling and unit conversion.
|
37 videos|12 docs|18 tests
|
FAQs on Ratio and Proportion - Year 9 Mathematics (Cambridge)
| 1. What is the difference between a ratio and a proportion? |  |
| 2. How can ratios be used in real-life scenarios? |  |
| 3. How can one simplify ratios to make them easier to work with? |  |
| 4. How can one determine if two ratios are proportional to each other? |  |
| 5. Can ratios be used to compare quantities of different units? |  |

















