Optimal File Merge Patterns | Algorithms - Computer Science Engineering (CSE) PDF Download
| Table of contents |

|
| Optimal File Merge Patterns |

|
| Concept |

|
| Strategy |

|
| Observations |

|
| Code Implementation |

|
Optimal File Merge Patterns
The Optimal Merge Pattern refers to a strategy for merging multiple sorted files into a single file with the minimum computational effort.
Concept
When you have several sorted files and you want to merge them into one single file, you can do this using the Optimal Merge Pattern to minimize the total computations needed.
Strategy
- Merge in Pairs: Start by merging the smallest files first.
- Greedy Approach: At each step, merge the two smallest available files. This ensures that the size of the files being merged remains as small as possible at each stage of the process.
- Repeat: Continue merging pairs of files until all files are merged into a single file.
Example: Given 3 files with sizes 2, 3, 4 units. Find an optimal way to combine these files
Input: n = 3, size = {2, 3, 4}
Output: 14
Explanation: There are different ways to combine these files:
Method 1: Optimal method 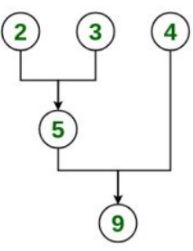 Cost = 5 + 9 = 14
Cost = 5 + 9 = 14
Method 2:  Cost = 7 + 9 = 16
Cost = 7 + 9 = 16
Method 3:
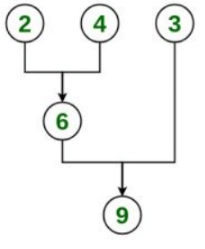 Cost = 6 + 9 = 15
Cost = 6 + 9 = 15
Observations
From the observations made, it becomes clear that to minimize the computation cost effectively, it's essential to always prioritize merging the smallest possible files first and continuously reduce the number of files in consideration. This optimal strategy can be efficiently implemented using a min-heap (priority queue) data structure.
Code Implementation
// C++ program to implement
// Optimal File Merge Pattern
#include <bits/stdc++.h>
using namespace std;
// Function to find minimum computation
int minComputation(int size, int files[])
{
// Create a min heap
priority_queue<int, vector<int>, greater<int> > pq;
for (int i = 0; i < size; i++) {
// Add sizes to priorityQueue
pq.push(files[i]);
}
// Variable to count total Computation
int count = 0;
while (pq.size() > 1) {
// pop two smallest size element
// from the min heap
int first_smallest = pq.top();
pq.pop();
int second_smallest = pq.top();
pq.pop();
int temp = first_smallest + second_smallest;
// Add the current computations
// with the previous one's
count += temp;
// Add new combined file size
// to priority queue or min heap
pq.push(temp);
}
return count;
}
// Driver code
int main()
{
// No of files
int n = 6;
// 6 files with their sizes
int files[] = { 2, 3, 4, 5, 6, 7 };
// Total no of computations
// do be done final answer
cout << "Minimum Computations = "
<< minComputation(n, files);
return 0;
}
Output:
Minimum Computations = 68
Time Complexity: O(nlogn)
Auxiliary Space: O(n)
|
81 videos|113 docs|34 tests
|
FAQs on Optimal File Merge Patterns - Algorithms - Computer Science Engineering (CSE)
| 1. What are optimal file merge patterns in the context of data processing? |  |
| 2. Why is it important to use optimal file merge patterns in data processing? |  |
| 3. What are some common file merge patterns used in data processing? |  |
| 4. How can one determine the optimal file merge pattern for a specific data processing task? |  |
| 5. Are there any tools or software available to help implement optimal file merge patterns in data processing? |  |




















