Poisson's Ratio | Strength of Materials (SOM) - Mechanical Engineering PDF Download
| Table of contents |

|
| Stress-strain Relationships and its Constant |

|
| Hooke’s Law |

|
| Relationship between the elastic constant |

|
| Solved Numericals |

|
Stress-strain Relationships and its Constant
Young’s Modulus
For the description of the elastic properties of linear objects like wires, rods, columns which are either stretched or compressed, a convenient parameter is the ratio of the stress to the strain, a parameter called the Young's modulus of the material. Young's modulus can be used to predict the elongation or compression of an object as long as the stress is less than the yield strength of the material.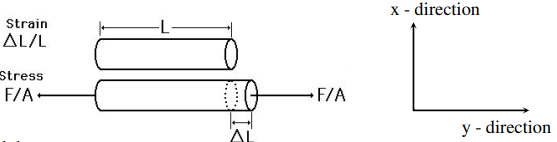
Young’s modulus :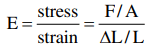
Hooke’s Law
Hooke's law simply states that the extension of a spring (or any other stretchable object) is directly proportional to the force acting on it.
This law is only true if the elastic limit of the object has not been reached. If the elastic limit has been reached the object will not return to its original shape and may eventually break.
Bulk Modulus of Elasticity: The Bulk Modulus of Elasticity (K) is a measure of a material's resistance to uniform compression. It represents the material's elastic response to hydrostatic pressure or equilateral tension, reflecting its volumetric response under such conditions.
Poisson's Ratio: Poisson's Ratio (v) is a measure of the elastic deformation of a material in directions perpendicular to the direction of loading. Specifically, it is the ratio of transverse strain to the corresponding axial strain when a material is subjected to uniaxial stress.
Consider a piece of material in 2-dimensions. The stress in the y direction is σy and there is no stress in the x-direction. When it is stretched in the y-direction, it causes the material to get thinner in all the other directions at right angles to it. This means that a negative strain is produced in the x-direction. For elastic materials, it is found that the applied strain (εy) is always directly proportional to the induced strain (εx) and its ratio is called Poisson’s Ratio.
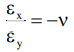
The strain produced in the x-direction is εx = - vεy
If stress is applied in x-direction then the resulting strain in the y-direction would similarly be εy= - νεx The resulting strain in any one direction is the sum of the strains due to the direct force and the induced strain from the other direct force.
The resulting strain in any one direction is the sum of the strains due to the direct force and the induced strain from the other direct force.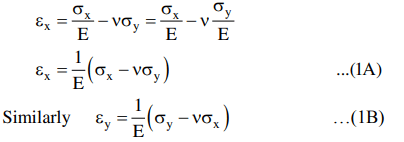
Converting Strain into Stress
We have already derived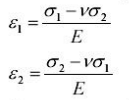

Relationship between the elastic constant
When the material is compressed by a pressure p the stress is equal to -p because it is compressive. The bulk modulus is then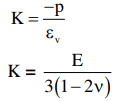 This shows the relation between E, K and ν.
This shows the relation between E, K and ν.
The relation between E, G and v is given by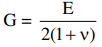 where E = Young’s modulus
where E = Young’s modulus
G = Bulk modulus
v = Poisson’s ratio
Solved Numericals
Q1. A student conducted an experiment on a wire and observed that there was no change in the volume of the wire due to a change in its length by stretching. The Poisson's ratio of the material of the wire is:Ans:
- Poisson's ratio: It is defined as the ratio of transverse strain to longitudinal strain in the direction of the stretching force.
- When a material is stretched in one direction, it tends to get compressed in the direction perpendicular to the direction of the force.
- Thus, a longitudinal strain causes a transverse strain and vice versa.
- Poisson's ratio is positive for tensile deformation and negative for compressive deformation.
- Poisson's ratio for any material lies in the range of 0 to 1.
Poisson's ratio, 
Where ϵt is the transverse strain and ϵl is the longitudinal strain.
Let the length of the wire be l, r its radius, and A its cross-sectional area.
Poisson's ratio, 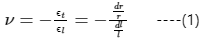
Volume of wire, V = Length × Cross-sectional area = l × πr2
dV = πr2.dl + 2πrl.dr
Since there is no change in volume, dV = 0
⇒ 0 = πr2.dl + 2πrl.dr
⇒ πr2.dl = - 2πrl.dr
Substituting (2) in (1),
Poisson's ratio, 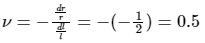
Q2. An experiment was conducted and it was found that shear modulus of the material is equal to the bulk modulus then what will be the value of Poisson’s ratio?
Ans:
Concept:
The relation between elastic modulus (E), Bulk modulus (K) and shear modulus (G) is given by
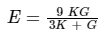
Also we have relation between E and G as E = 2G (1 + μ)
Now,
After combining these two equations we get

Calculation:
Given:
K = G
Now,
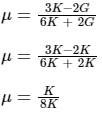
∴ μ = 0.125
Q3. A student conducted an experiment on a wire and observed that there was no change in the volume of the wire due to a change in its length by stretching. The Poisson's ratio of the material of the wire is:
Ans:
- Poisson's ratio: It is defined as the ratio of transverse strain to longitudinal strain in the direction of the stretching force.
- When a material is stretched in one direction, it tends to get compressed in the direction perpendicular to the direction of the force.
- Thus, a longitudinal strain causes a transverse strain and vice versa.
- Poisson's ratio is positive for tensile deformation and negative for compressive deformation.
- Poisson's ratio for any material lies in the range of 0 to 1.
Poisson's ratio, 
Where ϵt is the transverse strain and ϵl is the longitudinal strain.
Let the length of the wire be l, r its radius, and A its cross-sectional area.
Poisson's ratio, 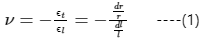
Volume of wire, V = Length × Cross-sectional area = l × πr2
dV = πr2.dl + 2πrl.dr
Since there is no change in volume, dV = 0
⇒ 0 = πr2.dl + 2πrl.dr
⇒ πr2.dl = - 2πrl.dr
Substituting (2) in (1),
Poisson's ratio, 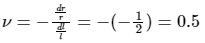
|
37 videos|39 docs|45 tests
|
FAQs on Poisson's Ratio - Strength of Materials (SOM) - Mechanical Engineering
| 1. What is the relationship between the elastic constants in stress-strain relationships? |  |
| 2. How can Poisson's Ratio be used to determine material properties in stress-strain relationships? |  |
| 3. What are some common values of elastic constants for different materials? |  |
| 4. How do stress-strain relationships and their constants play a role in material testing and design? |  |
| 5. Can the relationship between elastic constants be used to predict the failure of a material under stress? |  |

|
Explore Courses for Mechanical Engineering exam
|

|

















