Concept of Shear Centre | Strength of Materials (SOM) - Mechanical Engineering PDF Download
Introduction
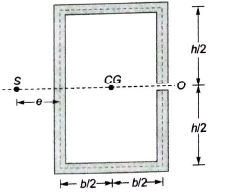
The shear centre is the point through which if the resultant shear force acts, then the member is subjected to simple bending without twisting. This means a load acting on a beam through the shear centre will produce bending without torsion. The shear centre is also known as the centre of flexure.Location of Shear Centre
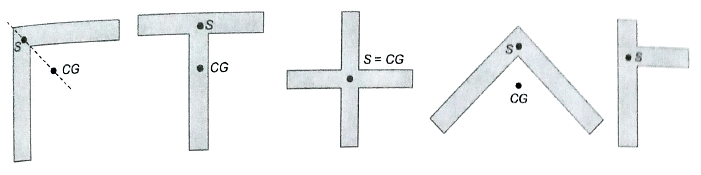
The shear centre generally does not coincide with the centroid of the section except in special cases where the area is symmetrical about both axes. The shear centre always lies on the axis of symmetry if it exists. If there are two or more axes of symmetry, then the shear centre will coincide with the point of intersection of the axes of symmetry, which means the shear centre of the area will be the same as the centroid of the area.

Shear Flow
Shear flow is the variation of shear force per unit length. The formula for longitudinal shear flow is:
Longitudinal shear flow = 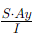
 Where:
Where:
- S = shear force
- Ay = moment of area under consideration about the neutral axis
- I = moment of inertia about the neutral axis
Shear Centres of Thin-Walled Open Sections
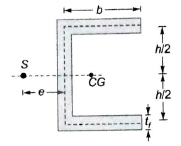
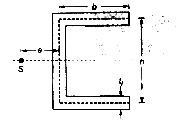
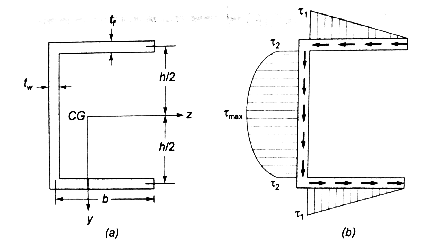
Channel Section: For a channel section bending about the z-axis and subjected to vertical shear force S parallel to the y-axis, the maximum shear stress in the flange is given by: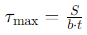
 Where:
Where:
- S = vertical shear force
- b = width of the flange
- t = thickness of the flange
The shear centre e from the centre line of the web is determined by: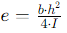 Where:
Where:
- h = height of the section
- I = moment of inertia about the neutral axis
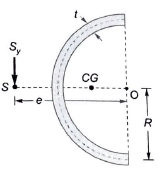
Thin-Walled Semicircular Cross-Section
For a thin-walled semicircular cross-section, the shear stress at an angle θ is given by:
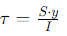
Where y is the moment of area under consideration about the neutral axis.
 The position of the shear centre e is given by:
The position of the shear centre e is given by:
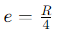
Where R is the radius of the semicircle.
Shear Centres of Some Important Sections
- Channel Section: The shear centre lies at a distance from the centre line of the web.

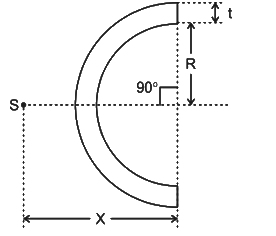
- Semi-Circular Section: The shear centre is located at 4R/3π from the centre of the arc.

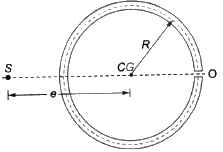
- Slit Circular Tube with Constant Thickness: The shear centre is at a distance of 2R / π from the centre of the tube.

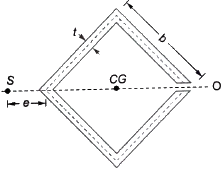
- Slit Square Tube: The shear centre lies at b / 2 from the centre of the tube, where b is the side length.

- Rectangular Tube of Constant Thickness having Slit at End: The shear centre is determined by the formula

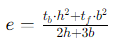 Where:
Where:
- tb = thickness of the base
- tf = thickness of the flange
- h = height
- b = width
Circular Arc: The shear centre is given by: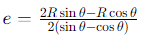 Where R is the radius of the arc and θ is the angle subtended by the arc.
Where R is the radius of the arc and θ is the angle subtended by the arc.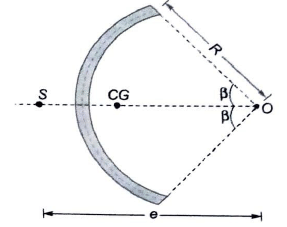 These equations and principles help determine the shear centre for various cross-sectional shapes, which is crucial for designing structures that avoid torsional effects under load.
These equations and principles help determine the shear centre for various cross-sectional shapes, which is crucial for designing structures that avoid torsional effects under load.
Solved Numericals
Q1. Find the approximate location of the shear center for a beam with the cross-section of the channel as shown in the figure. h = 250 mm, b = 130 mm, t = 3 mm. Choose the correct answer from the following options.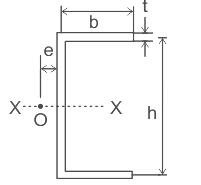 Solution:
Solution:
Shear Centre:It is the point (inside or outside a section) through which the applied shear force produces no torsion or twist of the member (or)
Shear Centre is defined as the point through which the load must be applied to produce zero twisting moment on the section. If load passes through the shear centre, then there will be only bending stress in the cross-section and no twisting.
The following points should be remembered for the shear centre:
- If a beam has two axes of symmetry, then the shear centre will lie at their point of intersection.
- For a section having one axis of symmetry, the shear centre lies on that axis of symmetry.
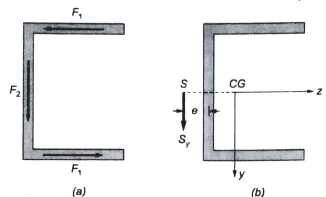
The shear flow in channel section causes clockwise twisting as shown.
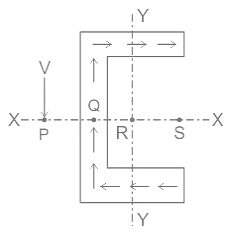 To balance that clockwise twisting, the external resultant load must cause anticlockwise twisting and it can be possible if load lies an LHS of the channel section.
To balance that clockwise twisting, the external resultant load must cause anticlockwise twisting and it can be possible if load lies an LHS of the channel section.
Further, since the channel section has X-X as of symmetry and Y-Y axis is not the symmetric axis so, ‘R’ cannot be shear centre.
‘S’, and ‘Q’ cannot be shear centre because they cause external loading twisting in clockwise rather than anticlockwise.
So, the only possible location of the shear centre is ‘P’.
Here Point P represents Shear centre ( Which is outside the body )
Shear centre for channel section
The location of the shear centre for a channel section is given by
 where,
where,
h = distance between the centre lines of the flanges
t = Thickness of the flange
b = Length of the flange up to the centreline of the web
Ixx = Moment of inertia of the channel about the axis of symmetry (X-X axis)
e = Horizontal distance of applied vertical downward shear force from the centre of the web
Calculation:
Given data
h = 250 mm, b = 130 mm, t = 3 mm
Ixx = 1.60960 x107 mm4
The location of the shear centre for a channel section is given by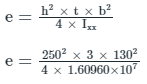
e = 49.216 mm
Q2. Shear centre of a semi-circular arc of radius r is at:
Solution: Shear center of a circular section is given by:
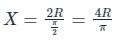
Q3. A cross-section of a slit circular tube of constant thickness is shown in the figure below. Calculate the distance 'e' from the center of the circle (C) to the shear center (S), if the radius r = 20 cm.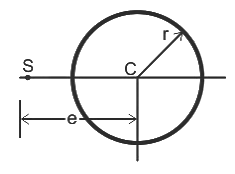 Solution: Given data:
Solution: Given data:
r = 20 cm
e = distance between the center of the circle (C) to the shear center (S)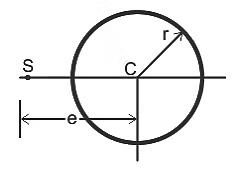
Now Shear center of the circular tube is given by the following formula:
e = 2r
e = 2 x 20
e = 40 cm
|
37 videos|39 docs|45 tests
|
FAQs on Concept of Shear Centre - Strength of Materials (SOM) - Mechanical Engineering
| 1. What is the concept of the shear centre in structural engineering? |  |
| 2. How is the shear centre different from the centroid of a cross-section? |  |
| 3. Why is the concept of the shear centre important in structural analysis? |  |
| 4. How can the shear centre be calculated for a given cross-section? |  |
| 5. What are the practical implications of understanding the shear centre in structural design? |  |

|
Explore Courses for Mechanical Engineering exam
|

|