Q1: The sum of the eigenvalues of the matrix 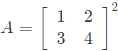 is _____ (rounded off to the nearest integer). (2024)
is _____ (rounded off to the nearest integer). (2024)
(a) 15
(b) 26
(c) 29
(d) 45
Ans: (c)
Sol:
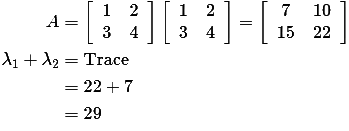
Q2: Which one of the following matrices has an inverse? (2024)
(a) 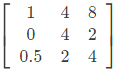
(b) 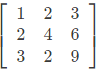
(c) 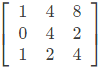
(d) 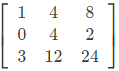
Ans: (c)
Sol:
Option :A
det = 0
Cannot have inverse.
Option : B
det = 0
Cannot have inverse.
Option : D
det = 0
It cannot have inverse.
Option : C
∣𝐴∣ ≠ 0
∴ It has inverse.
Q3: Consider a matrix A = 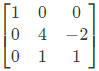
The matrix A satisfies the equation 6A-1 = A2 + cA + dI where c and d are scalars and I is the identity matrix. Then (c + d) is equal to (2022)
(a) 5
(b) 17
(c) -6
(d) 11
Ans: a
Sol: Characteristic equation:
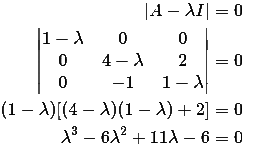 By cayley hamilton theorem
By cayley hamilton theorem
A3 - 6A2 + 11A - 6 = 0
A2 - 6A + 11I = 6A-1
On comparison : c = -6 and d = 11
Therefore, c + d = -6 + 11 = 5
Q4: eA denotes the exponential of a square matrix A. Suppose λ is an eigenvalue and v is the corresponding eigen-vector of matrix A.
Consider the following two statements: (2022)
Statement 1: eλ is an eigenvalue of eA .
Statement 2: 𝑣 is an eigen-vector of eA.
Which one of the following options is correct?
(a) Statement 1 is true and statement 2 is false.
(b) Statement 1 is false and statement 2 is true
(c) Both the statements are correct.
(d) Both the statements are false.
Ans: c
Sol: Eigen value will change but eigen vector not change.
Q5: Consider a 3 x 3 matrix A whose (i, j)-th element, ai, j = (i - j)3. Then the matrix A will be (2022)
(a) symmetric.
(b) skew-symmetric.
(c) unitary
(d) null.
Ans: (b)
Sol:
for i = j ⇒ aij = (i - i)3 = 0∀i
for i ≠ j ⇒ aij = (i - j)3 = (-(j - i))3 = - (j - i)3 = -aji
∴ A3×3 is skew symmetric matrix.
Q6: Let A be a 10 × 10 matrix such that A5 is a null matrix, and let I be the 10 × 10 identity matrix. The determinant of A + I is _______. (2021)
(a) 1
(b) 2
(c) 4
(d) 8
Ans: (a)
Sol: Given: A5 = 0
Ax = λx
⇒ A5x = λ5x (∵ x = 0)
⇒ λ5 = 0
⇒ λ = 0
Eigen values of A + I given λ + 1
∵ Eigen values of IA = 1
Hence |A + I| = Product of eigen values = 1 x 1 x 1 x .... 10 times
= 1
Q7: Let p and q be real numbers such that p2 + q2 = 1. The eigenvalues of the matrix  are (2021)
are (2021)
(a) 1 and 1
(b) 1 and -1
(c) j and -j
(d) pq and -pq
Ans: (b)
Sol: Characteristic equation of A
∣A2×2 − λI∣ = (−1)2 λ2 + (−1)1 Tr(A)λ + ∣A∣ = 0
λ2 −(p − p)λ + (−p2 − q2) = 0
⇒ λ2 - 1 = 0
⇒ λ = ± 1
Q8: The number of purely real elements in a lower triangular representation of the given 3 x 3 matrix, obtained through the given decomposition is (2020)
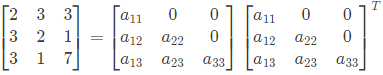 (a) 5
(a) 5
(b) 6
(c) 8
(d) 9
Ans: d
Sol: As per GATE official answer key MTA (Marks to ALL)
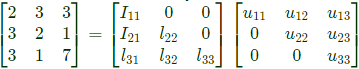 consider, u11 = u22 = u33 = 1
consider, u11 = u22 = u33 = 1
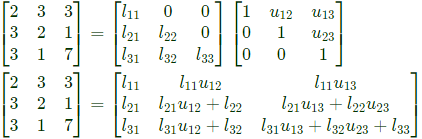

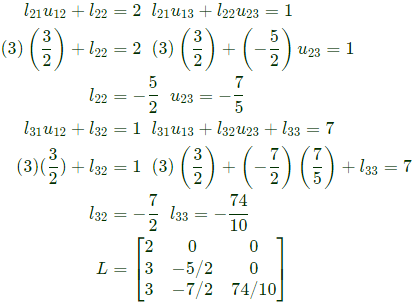 The number of purely real elements of lower triangular matrix are 9.
The number of purely real elements of lower triangular matrix are 9.
Q9: Consider a 2 x 2 matrix M = [v1 v2], where, v1 and v2 are the column vectors. Suppose 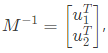 where
where 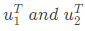 are the row vectors. Consider the following statements:
are the row vectors. Consider the following statements:
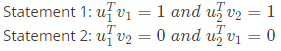 Which of thefollowing options is correct? (2019)
Which of thefollowing options is correct? (2019)
(a) Statement 1 is true and statement 2 is false
(b) Statement 2 is true and statement 1 is false
(c) Both the statements are true
(d) Both the statements are false
Ans: (c)
Sol:
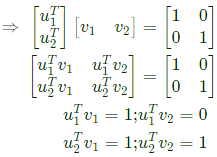 Statement (1) and (2) are both correct. Option (C) is correct.
Statement (1) and (2) are both correct. Option (C) is correct.
Q10: The rank of the matrix, 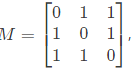 is ______ (2019)
is ______ (2019)
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (c)
Sol:
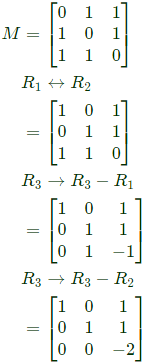 Which is in echelon form
Which is in echelon form
∴ ρ(A) = 3.
Q11: M is a 2 x 2 matrix with eigenvalues 4 and 9. The eigenvalues of M2 are (2019)
(a) 4 and 9
(b) 2 and 3
(c) -2 and -3
(d) 16 and 81
Ans: (d)
Sol: M is 2 x 2 matrix with eigen values 4 and 9. The eigen values of M2 are 16 and 81.
Q12: Let 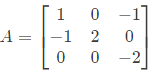 and B = A3 - A2 - 4A + 5I, where I is the 3 x 3 identity matrix. The determinant of B is _____ (up to 1 decimal place). (2018)
and B = A3 - A2 - 4A + 5I, where I is the 3 x 3 identity matrix. The determinant of B is _____ (up to 1 decimal place). (2018)
(a) 0.5
(b) 1.0
(c) 2.8
(d) 2.1
Ans: (b)
Sol:
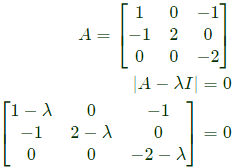 (1 − λ)((2 − λ)(−2 − λ))−1(0 − 0) = 0
(1 − λ)((2 − λ)(−2 − λ))−1(0 − 0) = 0
λ = 1, 2, −2
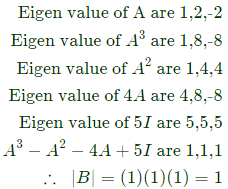
Q13: Consider a non-singular 2 x 2 square matrix A. If trace(A) = 4 and trace (𝐴2) = 5, the determinant of the matrix A is ______(up to 1 decimal place). (2018)
(a) 2.5
(b) 3.5
(c) 1.2
(d) 5.5
Ans: d
Sol: A is 2 x 2 matrix
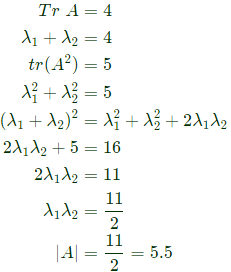
Q14: The eigen values of the matrix given below are 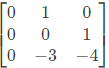 (SET-2 (2017))
(SET-2 (2017))
(a) (0, -1, -3)
(b) (0, -2, -3)
(c) (0, 2, 3)
(d) (0, 1, 3)
Ans: (a)
Sol: The characteristics equation is |A - λ|i = 0.
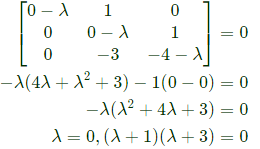 λ= -1, -3
λ= -1, -3
λ = (0, -1, -3)
Q15: The matrix 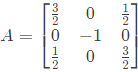 has three distinct eigenvalues and one of its eigenvectors is
has three distinct eigenvalues and one of its eigenvectors is 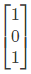 Which one of the following can be another eigenvector of A? (SET-1 (2017))
Which one of the following can be another eigenvector of A? (SET-1 (2017))
(a) 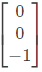
(b)
(c)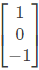
(d)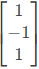
Ans: (c)
Sol: The given matrix is symmetric and all its eigen values are distinct. Hence all its eigen vectors are orthogonal one of the eigen vector is 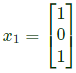 The corresponding orthogonal vector in the given option is C i.e.
The corresponding orthogonal vector in the given option is C i.e. 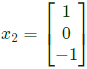
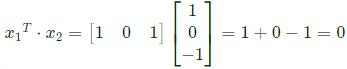
Q16: Let 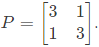 Consider the set S of all vectors
Consider the set S of all vectors  such that a2 + b2 = 1 where
such that a2 + b2 = 1 where 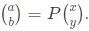 Then S is (SET-2 (2016))
Then S is (SET-2 (2016))
(a) a circle of radius √10
(b) a circle of radius 1/√10
(c) an ellipse with major axis along (1/1)
(d) an ellipse with minor axis along (1/1)
Ans: (d)
Sol:
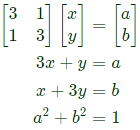 ⇒
⇒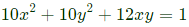
Ellipse with major axis along [1/1].
Q17: A 3 x 3 matrix P is such that, P3 = P. Then the eigenvalues of P are (SET-2(2016))
(a) 1, 1, -1
(b) 1, 0.5 + j0.866, 0.5 - j0.866
(c) 1, -0.5 + j0.866, -0.5 - j0.866
(d) 0, 1, -1
Ans: (a)
Sol: By Calyey Hamilton theorem,
λ3 = λ
λ = 0, 1, −1
Q18: Let A be a 4 x 3 real matrix with rank 2. Which one of the following statement is TRUE? (SET-1(2016))
(a) Rank of ATA is less than 2.
(b) Rank of ATA is equal to 2.
(c) Rank of ATA is greater than 2.
(d) Rank of ATA can be any number between 1 and 3.
Ans: (b)
Sol: Result,
Rank(ATA) = Rank(A)
Q19: Let the eigenvalues of a 2 x 2 matrix A be 1, -2 with eigenvectors x1 and x2 respectively. Then the eigenvalues and eigenvectors of the matrix A2 - 3A + 4l would, respectively, be (SET-1 (2016))
(a) 2, 14; x1, x2
(b) 2, 14; x1 + x2, x1 - x2
(c) 2, 0; x1, x2
(d) 2, 0; x1 + x2, x1 - x2
Ans: (a)
Sol: Eigen value of A2 − 3A + 4I are
(1)2 − 3(1) + 4 and (−2)2 − 3(−2) + 4
= 2, 14
Note: A2X = l2X
⇒ X is eigen vector for A2 corresponding to eigen value l2
X1 and X2 are eigen vector of A corresponding to 1, -2
Then X1 and X2 are eigen vector of 𝐴2 − 3 + 4𝐼 corresponding to 2, 14.
Q20: Consider a 3 x 3 matrix with every element being equal to 1. Its only non-zero eigenvalue is ____. (SET-1(2016))
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (c)
Sol:
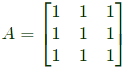 Eigen value are 0,0,3.
Eigen value are 0,0,3.
Q21: We have a set of 3 linear equations in 3 unknowns. 'X ≡ Y' means X and Y are equivalent statements and 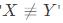 means X and Y are not equivalent statements.
means X and Y are not equivalent statements.
P : There is a unique solution.
Q : The equations are linearly independent.
R : All eigenvalues of the coefficient matrix are nonzero.
S : The determinant of the coefficient matrix is nonzero.
Which one of the following is TRUE? (SET-2(2015))
(a) P ≡ Q ≡ R ≡ S
(b) 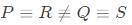
(c) 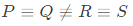
(d) 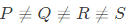
Ans: (a)
Sol:
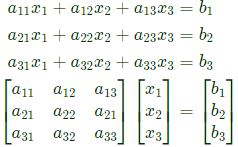
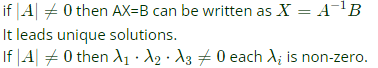 If
If 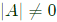 then all the row (column) vectors of A are linearly independent.
then all the row (column) vectors of A are linearly independent.
Q22: The maximum value of "a" such that the matrix 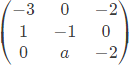 has three linearly independent real eigenvectors is (SET-1(2015))
has three linearly independent real eigenvectors is (SET-1(2015))
(a)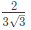
(b)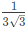
(c)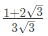
(d)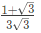
Ans: (b)
Q23: If the sum of the diagonal elements of a 2 x 2 matrix is -6, then the maximum possible value of determinant of the matrix is ________. (SET-1(2015))
(a) 6
(b) 8
(c) 9
(d) 12
Ans: (c)
Sol: Consider a symmetric matrix 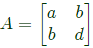
Given a + d = −6
∣A∣ = ad − b2
Now since b2 is always non-negative, maximum determinant will come when b2 = 0.
So we need to maximize
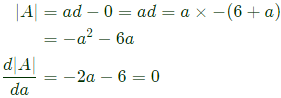 ⇒ a = -3 is the only stationary point
⇒ a = -3 is the only stationary point
Since, 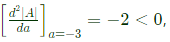 we have a maximum at a = −3.
we have a maximum at a = −3.
Since a + d = −6, corresponding value of 𝑑 = −3.
∣A∣ = ad = −3 × −3 = 9.
Q24: Two matrices A and B are given below:
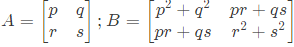 If the rank of matrix A is N, then the rank of matrix B is (SET-3 (2014))
If the rank of matrix A is N, then the rank of matrix B is (SET-3 (2014))
(a) N/2
(b) N-1
(c) N
(d) 2N
Ans: (c)
Sol:
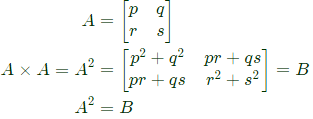 Rank of amtrix does not change when we squaring the matrix, hence rank of B = rank of A = N.
Rank of amtrix does not change when we squaring the matrix, hence rank of B = rank of A = N.
Q25: Which one of the following statements is true for all real symmetric matrices? (SET-2 (2014))
(a) All the eigenvalues are real.
(b) All the eigenvalues are positive.
(c) All the eigenvalues are distinct.
(d) Sum of all the eigenvalues is zero.
Ans: (a)
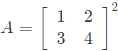 is _____ (rounded off to the nearest integer). (2024)
is _____ (rounded off to the nearest integer). (2024)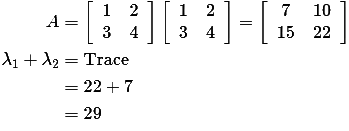
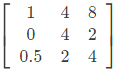
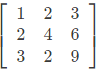
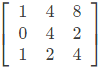
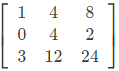
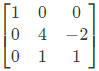
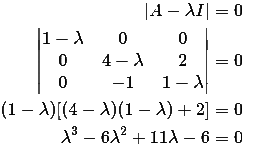 By cayley hamilton theorem
By cayley hamilton theorem are (2021)
are (2021)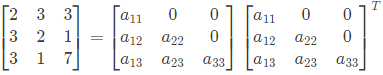 (a) 5
(a) 5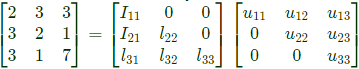 consider, u11 = u22 = u33 = 1
consider, u11 = u22 = u33 = 1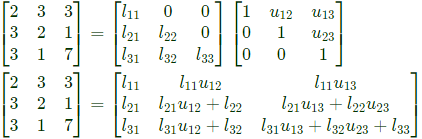

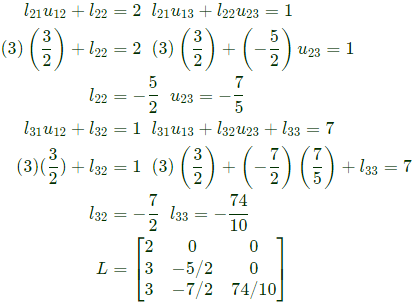 The number of purely real elements of lower triangular matrix are 9.
The number of purely real elements of lower triangular matrix are 9.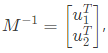 where
where 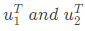 are the row vectors. Consider the following statements:
are the row vectors. Consider the following statements: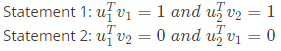 Which of thefollowing options is correct? (2019)
Which of thefollowing options is correct? (2019)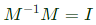
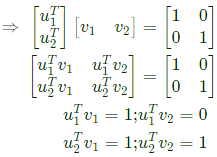 Statement (1) and (2) are both correct. Option (C) is correct.
Statement (1) and (2) are both correct. Option (C) is correct.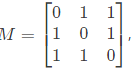 is ______ (2019)
is ______ (2019)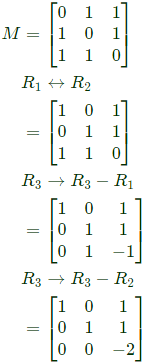 Which is in echelon form
Which is in echelon form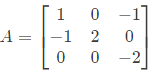 and B = A3 - A2 - 4A + 5I, where I is the 3 x 3 identity matrix. The determinant of B is _____ (up to 1 decimal place). (2018)
and B = A3 - A2 - 4A + 5I, where I is the 3 x 3 identity matrix. The determinant of B is _____ (up to 1 decimal place). (2018)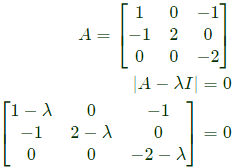 (1 − λ)((2 − λ)(−2 − λ))−1(0 − 0) = 0
(1 − λ)((2 − λ)(−2 − λ))−1(0 − 0) = 0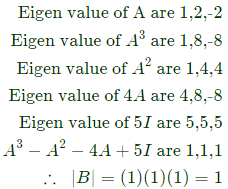
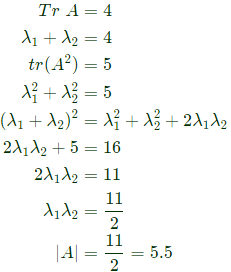
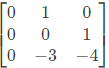 (SET-2 (2017))
(SET-2 (2017))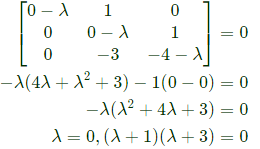 λ= -1, -3
λ= -1, -3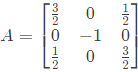 has three distinct eigenvalues and one of its eigenvectors is
has three distinct eigenvalues and one of its eigenvectors is 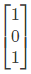 Which one of the following can be another eigenvector of A? (SET-1 (2017))
Which one of the following can be another eigenvector of A? (SET-1 (2017))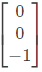

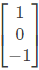
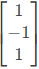
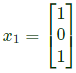 The corresponding orthogonal vector in the given option is C i.e.
The corresponding orthogonal vector in the given option is C i.e. 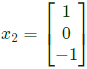
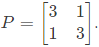 Consider the set S of all vectors
Consider the set S of all vectors  such that a2 + b2 = 1 where
such that a2 + b2 = 1 where 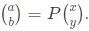 Then S is (SET-2 (2016))
Then S is (SET-2 (2016))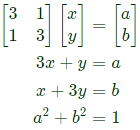 ⇒
⇒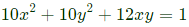
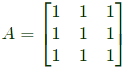 Eigen value are 0,0,3.
Eigen value are 0,0,3.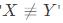 means X and Y are not equivalent statements.
means X and Y are not equivalent statements.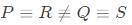
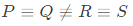
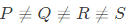
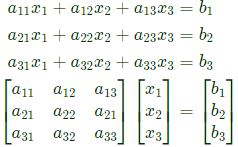
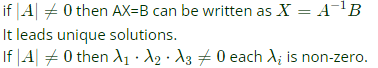 If
If 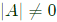 then all the row (column) vectors of A are linearly independent.
then all the row (column) vectors of A are linearly independent.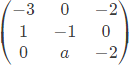 has three linearly independent real eigenvectors is (SET-1(2015))
has three linearly independent real eigenvectors is (SET-1(2015))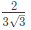
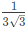
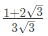
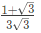
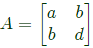
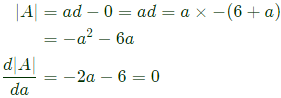 ⇒ a = -3 is the only stationary point
⇒ a = -3 is the only stationary point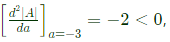 we have a maximum at a = −3.
we have a maximum at a = −3. 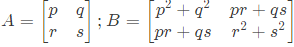 If the rank of matrix A is N, then the rank of matrix B is (SET-3 (2014))
If the rank of matrix A is N, then the rank of matrix B is (SET-3 (2014))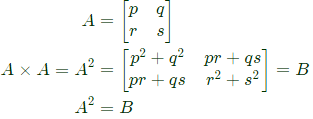 Rank of amtrix does not change when we squaring the matrix, hence rank of B = rank of A = N.
Rank of amtrix does not change when we squaring the matrix, hence rank of B = rank of A = N.

























