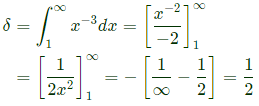Q31: The mean thickness and variance of silicon steel laminations are 0.2 mm and 0.02 respectively. The varnish insulation is applied on both the sides of the laminations. The mean thickness of one side insulation and its variance are 0.1 mm and 0.01 respectively. If the transformer core is made using 100 such varnish coated laminations, the mean thickness and variance of the core respectively are (SET-3(2014))
(a) 30 mm and 0.22
(b) 30 mm and 2.44
(c) 40 mm and 2.44
(d) 40 mm and 0.24
Ans: (d)
Q32: Integration of the complex function  in the counterclockwise direction, around |z - 1| = 1, is (SET-3(2014))
in the counterclockwise direction, around |z - 1| = 1, is (SET-3(2014))
(a) −πi
(b) 0
(c) πi
(d) 2πi
Ans: (c)
Sol: 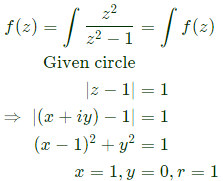
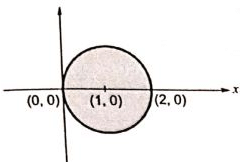 Poles of f(z)
Poles of f(z)
z2−1 = 0
[z = +1, 1]
So, −1 → Outside circle +1 → Inside circle
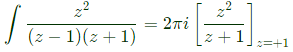
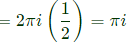
 as it lies outside from counter.
as it lies outside from counter.
Q33: Let ▽⋅(fv) = x2y + y2z + z2x, where f and v are scalar and vector fields respectively. If v = yi + zj + xk, then v⋅▽f is (SET-3 (2014))
(a) x2y + y2z + z2x
(b) 2xy + 2yz + 2zx
(c) x + y + z
(d) 0
Ans: (a)
Sol: 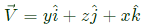
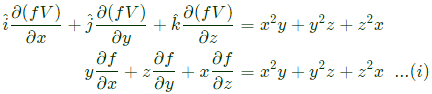
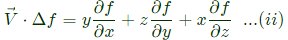
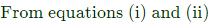

Q34: A particle, starting from origin at t = 0s, is traveling along x-axis with velocity 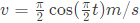
At t = 3s, the difference between the distance covered by the particle and the magnitude of displacement from the origin is_____ (SET-3(2014))
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (b)
Q35: The minimum value of the function f(x) = x3 − 3x2 − 24x + 100 in the interval [-3, 3] is (SET-2 (2014))
(a) 20
(b) 28
(c) 16
(d) 32
Ans: (b)
Sol: 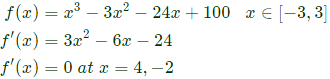 Critical points are [-3, -2, 3]
Critical points are [-3, -2, 3]
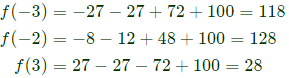 Hence f(x) has minimum value at x = 3 which is 28.
Hence f(x) has minimum value at x = 3 which is 28.
Q36: To evaluate the double integral 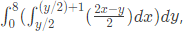 we make the substitution
we make the substitution 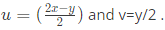 The integral will reduce to (SET-2(2014))
The integral will reduce to (SET-2(2014))
(a) 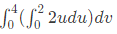
(b) 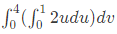
(c) 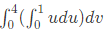
(d) 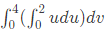
Ans: (b)
Sol: 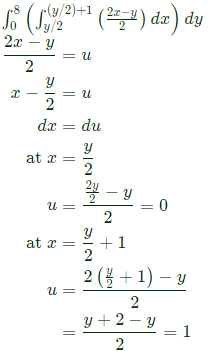 Thus, integral becomes
Thus, integral becomes 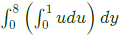
v = y/2
dv = dy/2
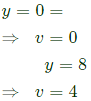
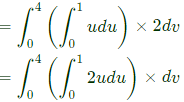
Q37: Minimum of the real valued function f(x) = (x − 1)2/3 occurs at x equal to (SET-2(2014))
(a) −∞
(b) 0
(c) 1
(d) ∞
Ans: (c)
Sol: 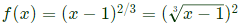 As f(x) is square of
As f(x) is square of 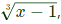 hence its minimum value be 0 where at x = 1.
hence its minimum value be 0 where at x = 1.
Q38: The line integral of function F = yzi, in the counterclockwise direction, along the circle x2 + y2 = 1 at z = 1 is (SET-1(2014))
(a) -2π
(b) -π
(c) π
(d) 2π
Ans: (b)
Sol: 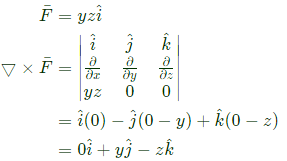 By strokes theoram,
By strokes theoram,
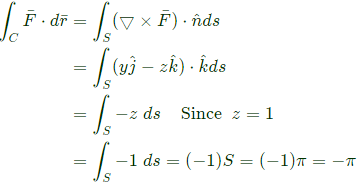 where S is surface area of x2 + y2 = 1
where S is surface area of x2 + y2 = 1
∴ S = π(1)2 = π
Q39: Let f(x) = xe−x. The maximum value of the function in the interval (0, ∞) is (SET-1(2014))
(a) e-1
(b) e
(c) 1 - e-1
(d) 1 + e-1
Ans: (a)
Sol: 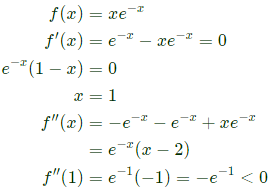 Hence f(x) has maximum value at x = 1
Hence f(x) has maximum value at x = 1
f(1) = 1⋅e−1= e−1
Q40: A function y = 5x2 + 10x is defined over an open interval x = (1, 2). Atleast at one point in this interval, dy/dx is exactly (2013)
(a) 20
(b) 25
(c) 30
(d) 35
Ans: (b)
Sol: 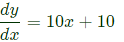
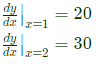 ∵ x is defined open interval x = (1, 2)
∵ x is defined open interval x = (1, 2)
∴ 1 < x < 2
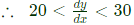
Q41. Given a vector field F = y2xax − yzay − x2az, the line integral ∫F⋅dl evaluated along a segment on the x-axis from x = 1 to x = 2 is (2013)
(a) -2.33
(b) 0
(c) 2.33
(d) 7
Ans: (b)
Sol: To find: 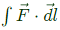 along a segment on the x-axis from x = 1 and x = 2.
along a segment on the x-axis from x = 1 and x = 2.
i.e. Y = 0, z = 0, dy = 0 and dz = 0
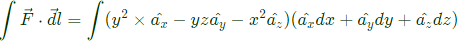
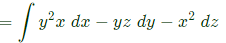 Putting y = 0, z = 0, dy = 0 and dz = 0, we get
Putting y = 0, z = 0, dy = 0 and dz = 0, we get 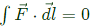
Q42: The curl of the gradient of the scalar field defined by V = 2x2y + 3y2z + 4z2x is (2013)
(a) 4xyax + 6yzax + 8zxaz
(b) 4ax + 6ax + 8az
(c) (4xy + 4z2)ax + (2x2 + 6yz)ax + (3y2 + 8zx)az
(d) 0
Ans: (d)
Sol: Curl of gradient of a scalar field is always zero.
▽ × ▽V = 0
Q43: The maximum value of f(x) = x3 − 9x2 + 24x + 5 in the interval [1, 6] is (2012)
(a) 21
(b) 25
(c) 41
(d) 46
Ans: (c)
Sol: We need absolute maximum of
f(x) = x3 − 9x2 + 24x + 5 in the interval of [1, 6]
First find local maximum if any by putting f'(x) = 0.
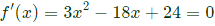
 x = 2, 4
x = 2, 4
Now
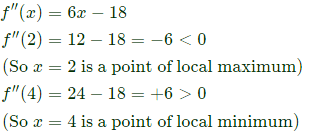 Now tabulate the value of f at end point of interval and at local maximum point, to find absolute maximum in given range, as shown below
Now tabulate the value of f at end point of interval and at local maximum point, to find absolute maximum in given range, as shown below
 Clearly the absolute maxima is at x=6 and absolute maximum value is 41.
Clearly the absolute maxima is at x=6 and absolute maximum value is 41.
Q44: The two vectors [1, 1, 1] and [1, a, a2] where 𝑎 = 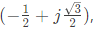 are (2011)
are (2011)
(a) Orthonormal
(b) Orthogonal
(c) Parallel
(d) Collinear
Ans: (b)
Sol: Given [1, 1, 1] and [1, a, a2]
hence 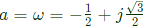
a2 = ω2
So the vectors we have
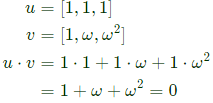 So u and v are orthogonal.
So u and v are orthogonal.
Q45: The function f(x) = 2x − x2 + 3 has (2011)
(a) a maxima at x = 1 and minimum at x = 5
(b) a maxima at x = 1 and minimum at x =- 5
(c) only maxima at x = 1
(d) only a minimum at x = 5
Ans: (c)
Sol: 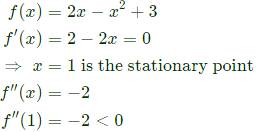 So at x = 1 we have a relative maxima.
So at x = 1 we have a relative maxima.
Q46: Roots of the algebraic equation x3 + x2 + x + 1 = 0 are (2011)
(a) (+1, +j, -j)
(b) (+1, -1, +1)
(c) (0, 0, 0)
(d) (-1, +j, -j)
Ans: (d)
Sol: −1 is one of the root since
(−1)3+(−1)2+(−1) + 1 = 0
By polynomial division
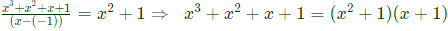 So root are (-1, +j, -j)
So root are (-1, +j, -j)
Q47: At t = 0, the function f(t) = (sint/t) has (2010)
(a) a minimum
(b) a discontinuity
(c) a point of inflection
(d) a maximum
Ans: (d)
Q48: Divergence of the three-dimensional radial vector field 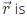 (2010)
(2010)
(a) 3
(b) 1/r
(c) 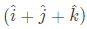
(d) 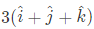
Ans: (a)
Sol: 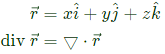
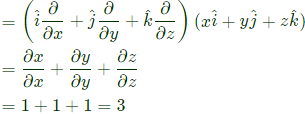
Q49: The value of the quantity P, where 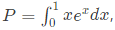 is equal to (2010 )
is equal to (2010 )
(a) 0
(b) 1
(c) e
(d) 1/e
Ans: (b)
Sol: 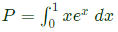 Integrating by parts:
Integrating by parts:
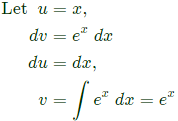
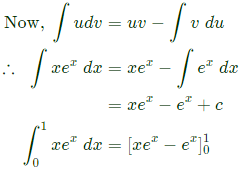
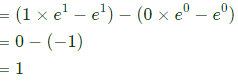
Q50: 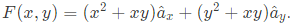 It's line integral over the straight line from (x, y) = (0, 2) to (x, y) = (2, 0) evaluates to (2009)
It's line integral over the straight line from (x, y) = (0, 2) to (x, y) = (2, 0) evaluates to (2009)
(a) -8
(b) 4
(c) 8
(d) 0
Ans: (d)
Sol: 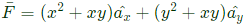
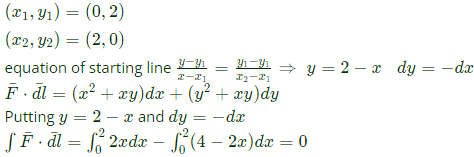
Q51: A cubic polynomial with real coefficients (2009)
(a) Can possibly have no extrema and no zero crossings
(b) May have up to three extrema and upto 2 zero crossings
(c) Cannot have more than two extrema and more than three zero crossings
(d) Will always have an equal number of extrema and zero crossings
Ans: (c)
Q52: f(x, y) is a continuous function defined over (x, y) ∈ [0, 1] × [0, 1]. Given the two constraints, x > y2 and y > x2, the volume under f(x, y) is (2009)
(a) 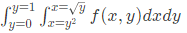
(b) 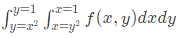
(c) 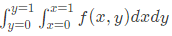
(d) 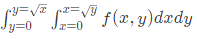
Ans: (a)
Sol: 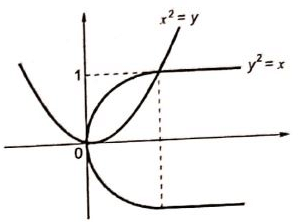
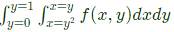
Q53: Consider function f(x) = (x2−4)2 where x is a real number. Then the function has (2008)
(a) only one minimum
(b) only tw0 minima
(c) three minima
(d) three maxima
Ans: (b)
Sol: 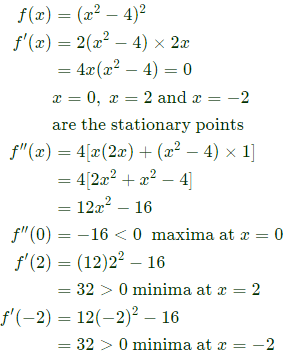 Therefore, there is only one maxima and only two minima for this function.
Therefore, there is only one maxima and only two minima for this function.
Q54: The integral  (2007)
(2007)
(a) sin t cos t
(b) 0
(c) (1/2)cos t
(d) (1/2) sin t
Ans: (b)
Sol: By property of infinite integral, 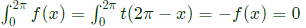
Q55: 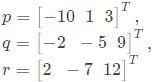 are three Vectors.
are three Vectors.
The following vector is linearly dependent upon the orthogonal set of vectors having a span that contains p, q, r is (2006)
(a) [8 9 3]T
(b) [−2 −17 30]T
(c) [4 4 5]T
(d) [13 2 −3]T
Ans: (d)
Q56: 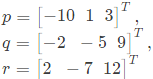 are three Vectors.
are three Vectors.
An orthogonal set of vectors having a span that contains p, q, r is (2006)
(a) [−6 −3 6]T, [4 −2 3]T
(b) [−4 2 4]T, [5 7 −11]T, [8 2 −3]T
(c) [6 7 −1] T, [−3 12 −2] T , [3 9 −4]T
(d) [4 3 11] T, [1 31 3] T, [5 3 4] T
Ans: (d)
Q57: A surface S(x, y) = 2x + 5y - 3 is integrated once over a path consisting of the points that satisfy (x+1)2+(y−1)2 = √2 . The integral evaluates to (2006)
(a) 17√2
(b) 17/√2
(c) √2/17
(d) 0
Ans: (d)
Q58: The expression 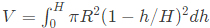 for the volume of a cone is equal to (2006)
for the volume of a cone is equal to (2006)
(a) 
(b) 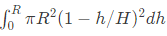
(c) 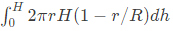
(d) 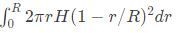
Ans: (d)
Sol: We have consider option (A) and (D) only because which contains variable r.
By integrating (D), we get
(1/3) πr2H, which is volume of cone.
Q59: For the scalar field 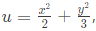 magnitude of the gradient at the point (1, 3) is (2005)
magnitude of the gradient at the point (1, 3) is (2005)
(a) √13/9
(b) √9/2
(c) √5
(d) 9/2
Ans: (c)
Sol: 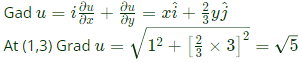
Q60: For the function f(x) = x2ex, the maximum occurs when x is equal to (2005)
(a) 2
(b) 1
(c) 0
(d) -1
Ans: (a)
Sol: 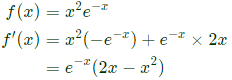
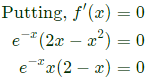 x = 0 or x = 2 are the stationary points.
x = 0 or x = 2 are the stationary points.
Now,
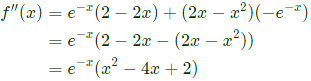
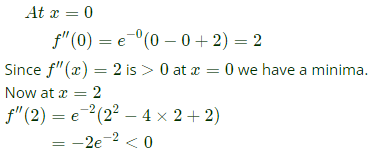 ∴ At x = 2 we have a maxima.
∴ At x = 2 we have a maxima.
Q61: If 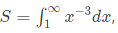 then S has the value (2005)
then S has the value (2005)
(a) -(1/3)
(b) 1/4
(c) 1/2
(d) 1
Ans: (c)
Sol: 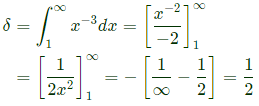
 in the counterclockwise direction, around |z - 1| = 1, is (SET-3(2014))
in the counterclockwise direction, around |z - 1| = 1, is (SET-3(2014))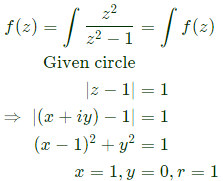
 Poles of f(z)
Poles of f(z)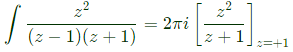
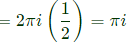
 as it lies outside from counter.
as it lies outside from counter.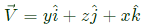
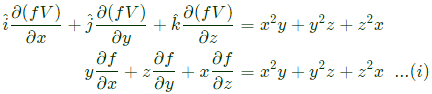
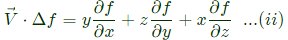

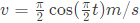
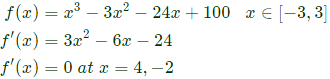 Critical points are [-3, -2, 3]
Critical points are [-3, -2, 3]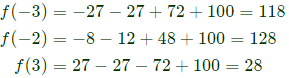 Hence f(x) has minimum value at x = 3 which is 28.
Hence f(x) has minimum value at x = 3 which is 28.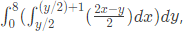 we make the substitution
we make the substitution 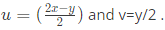 The integral will reduce to (SET-2(2014))
The integral will reduce to (SET-2(2014))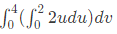
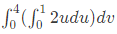
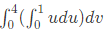
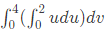
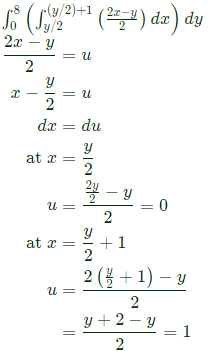 Thus, integral becomes
Thus, integral becomes 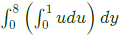
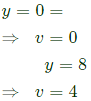
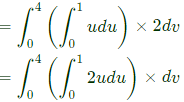
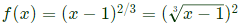 As f(x) is square of
As f(x) is square of 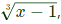 hence its minimum value be 0 where at x = 1.
hence its minimum value be 0 where at x = 1.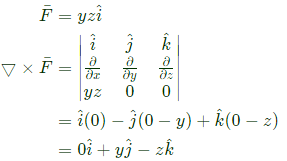 By strokes theoram,
By strokes theoram,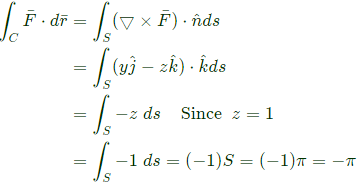 where S is surface area of x2 + y2 = 1
where S is surface area of x2 + y2 = 1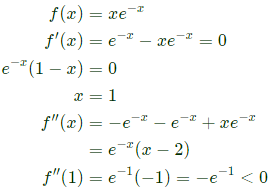 Hence f(x) has maximum value at x = 1
Hence f(x) has maximum value at x = 1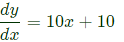
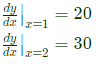 ∵ x is defined open interval x = (1, 2)
∵ x is defined open interval x = (1, 2)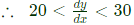
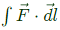 along a segment on the x-axis from x = 1 and x = 2.
along a segment on the x-axis from x = 1 and x = 2.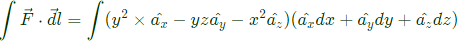
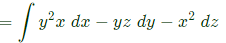 Putting y = 0, z = 0, dy = 0 and dz = 0, we get
Putting y = 0, z = 0, dy = 0 and dz = 0, we get 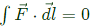
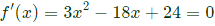
 x = 2, 4
x = 2, 4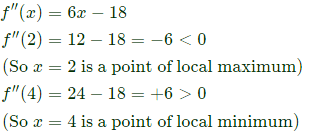 Now tabulate the value of f at end point of interval and at local maximum point, to find absolute maximum in given range, as shown below
Now tabulate the value of f at end point of interval and at local maximum point, to find absolute maximum in given range, as shown below Clearly the absolute maxima is at x=6 and absolute maximum value is 41.
Clearly the absolute maxima is at x=6 and absolute maximum value is 41.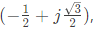 are (2011)
are (2011)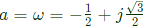
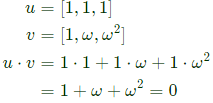 So u and v are orthogonal.
So u and v are orthogonal.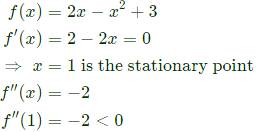 So at x = 1 we have a relative maxima.
So at x = 1 we have a relative maxima.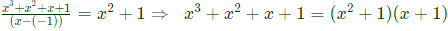 So root are (-1, +j, -j)
So root are (-1, +j, -j) (2010)
(2010)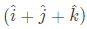
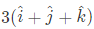
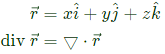
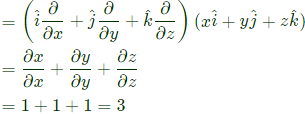
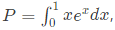 is equal to (2010 )
is equal to (2010 )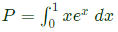 Integrating by parts:
Integrating by parts: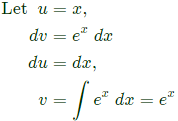
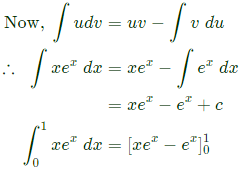
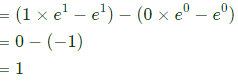
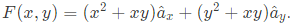 It's line integral over the straight line from (x, y) = (0, 2) to (x, y) = (2, 0) evaluates to (2009)
It's line integral over the straight line from (x, y) = (0, 2) to (x, y) = (2, 0) evaluates to (2009)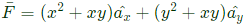
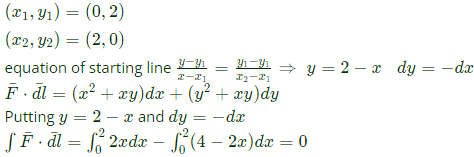
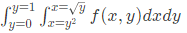
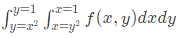
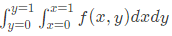
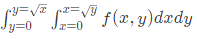

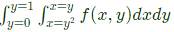
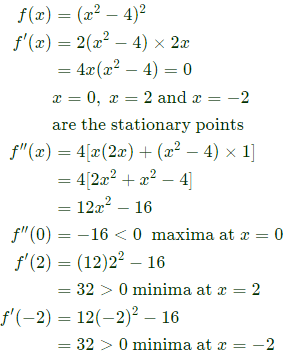 Therefore, there is only one maxima and only two minima for this function.
Therefore, there is only one maxima and only two minima for this function. (2007)
(2007)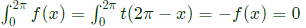
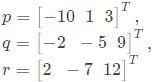 are three Vectors.
are three Vectors.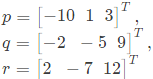 are three Vectors.
are three Vectors.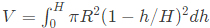 for the volume of a cone is equal to (2006)
for the volume of a cone is equal to (2006)
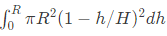
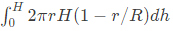
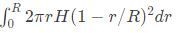
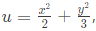 magnitude of the gradient at the point (1, 3) is (2005)
magnitude of the gradient at the point (1, 3) is (2005)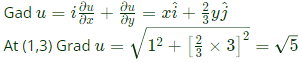
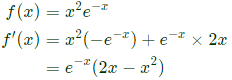
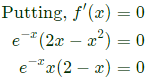 x = 0 or x = 2 are the stationary points.
x = 0 or x = 2 are the stationary points.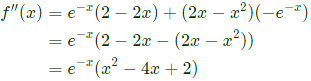
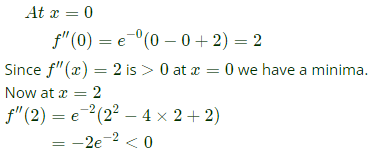 ∴ At x = 2 we have a maxima.
∴ At x = 2 we have a maxima.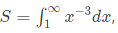 then S has the value (2005)
then S has the value (2005)