Congruence and Similarity of Triangles | Quantitative Aptitude for SSC CGL PDF Download
Geometry is a crucial subject in SSC Quantitative Aptitude, focusing on shapes and sizes. To excel in this area, one must master the fundamentals, theorems, and practical applications. This document will delve into the similarities and equalities between triangles, a fundamental part of Geometry in SSC.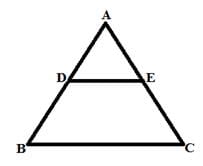
Congruence and similarity of triangles for SSC
- Two triangles are considered the same in both shape and size to be called congruent. This means that if the sides and angles of two triangles match up, they are congruent.
- Two triangles are called similar if they share the same shape. This implies that if the angles match and the sides are in proportion, the triangles are similar.
CPCTC: Corresponding Parts of Congruent Triangles are Congruent
Conditions for Congruence of Triangles
1. SSS (Side-Side-Side):
Corresponding sides are equal.
In △ABC and △DEF,
AB = FE, BC = ED and DF = CA
Hence △ABC ≅ △FED
2. SAS (Side-Angle-Side):
Two corresponding sides and the corresponding angle between them are equal.

In △ABC and △DEF,
AB = FE, DF = CA and ∠A = ∠F
Hence △ABC ≅ △FED
3. AAS(Angle-Angle-Side):
Two corresponding angles and the corresponding side which is not between them are equal.
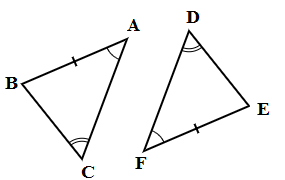
In △ABC and △DEF,
AB = FE, ∠C = ∠D and ∠A = ∠F
Hence △ABC ≅ △FED
4. ASA (Angle-Side-Angle):
Two corresponding angles and the corresponding side between them are equal.
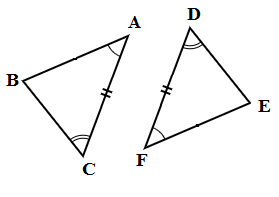
In △ABC and △DEF,
AC = FD, ∠C = ∠D and ∠A = ∠F
Hence △ABC ≅ △FED
5. RHS (Right-Hypotenuse-Side):
Hypotenuse and a pair of corresponding angles are equal in two right triangles.
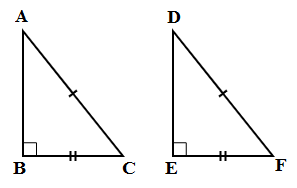
In △ABC and △DEF,
∠B = ∠E = 900, AC = DF and BC = EF
Hence △ABC ≅ △DEF
Conditions for Similarity of Triangles
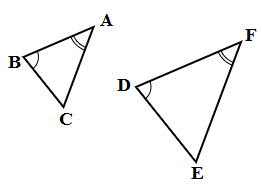
1. AA (Angle-Angle):
Two pairs of corresponding angles are equal.
△ABC and △FDE are similar
2. SAS (Side-Angle-Side):
Two pairs of corresponding sides are proportional and the angle between them is equal.

△ABC and △DEF are similar
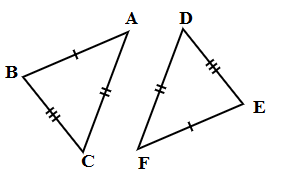
3. SSS (Side-Side-Side):
Corresponding sides are proportional.

AB/FD = BC/DE = AC/FE
△ABC and △FDE are similar
Note: If two triangles are similar then,
1. Ratio of area of the two triangles = Ratio of squares of corresponding sides
2. Ratio of sides of two triangles
= Ratio of their heights/altitudes
= Ratio of their medians
= Ratio of their angle bisectors
= Ratio of their in-radii/circum-radii
= Ratio of their perimeters
The conditions given above form the backbone for the preparation Congruence and similarity of triangles for SSC exams. Learning them is a must! Let us look at some theorems based on Congruence and similarity of triangles for SSC exams.
Congruence and similarity of triangles for SSC: Some Important Theorems
1. Basic Proportionality Theorem:
A line parallel to a side of a triangle divides the other two sides in the same ratio.
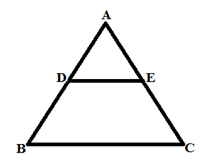
If DE ││ BC then,
AD/DB = AE/EC
Example: Area of quadrilateral DECB is 180 cm2 and DE divides AC in the ratio 2:5. If DE ││ BC, what is the area of △ADE?
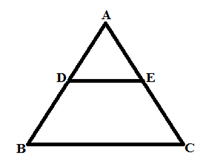
a) 16 cm2
b) 32 cm2
c) 40 cm2
d) 20 cm2
Answer: a
Solution:
AE/EC = 2/5 (DE divides AC in the ratio 2:5)
AE/EC = AD/DB (Basic Proportionality Theorem)
=> AE/EC = AD/AB = 2/7 and ∠DAE =∠BAC
=> △ADE and △ABC are similar. (By SAS Similarity Rule)
Area of △ADE / Area of △ABC = (2/7)2 = 4/49
Let area of △ADE = 4x then, area of △ABC = 49 x
Area of △ABC = Area of △ADE + Area of quadrilateral DCEB
49 x = 4x + 180
45 x = 180
x = 4
Area of △ADE = 4 x = 16 cm2
2. Angle Bisector Theorem:
The angle bisector divides the side in the ratio of remaining two sides.
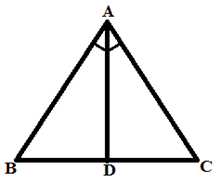
If AD bisects ∠A then, BD/DC = AB/AC
Example: If AD bisects ∠BAC and AD divides BC in the ratio 1:1 then, the ratio of area of △ABC to the area of △ABD is:
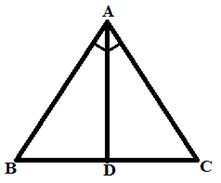
a) 3:1
b) 4:1
c) 3:2
d) 2:1
Answer : d
Solution:
BD/DC = AB/AC = 1
=> AB = AC and BD = DC
Also, AD = AD (common side)
△ABD ≅ △ACD (By SSS Congruence Rule)
Area of △ABC = Area of △ABD + Area of △ACD
= 2 Area of △ABD (Since, area of congruent triangles are equal)
Required ratio = 2:1
|
314 videos|170 docs|185 tests
|
FAQs on Congruence and Similarity of Triangles - Quantitative Aptitude for SSC CGL
| 1. What is the difference between congruence and similarity of triangles? |  |
| 2. How can we prove two triangles are congruent? |  |
| 3. What are some important theorems related to congruence and similarity of triangles? |  |
| 4. How can we determine if two triangles are similar? |  |
| 5. Can two triangles be congruent and similar at the same time? |  |
|
314 videos|170 docs|185 tests
|

|
Explore Courses for SSC CGL exam
|

|