Previous Year Questions: Minimum Spanning Tree | Algorithms - Computer Science Engineering (CSE) PDF Download
Q1: The number of distinct minimum-weight spanning trees of the following graph is _______ (2024 SET-2)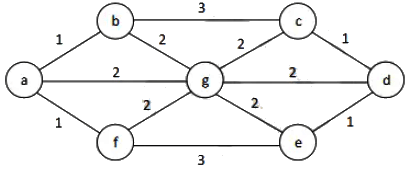
(a) 9
(b) 8
(c) 10
(d) 6
Ans: (a)
Sol: As we know, for the Min-Weight Spanning Tree of given graph, we will have 6 edges as the number of vertices are 7.
We want to find all the possible number of MSTs. So, in all the MSTs, "1" weights will be included making 4 edges.
Now, for the remaining 2 edges we have 6 choices respectively but these 6 choices will be as 3 choices for one edge and 3 choices for the other edge.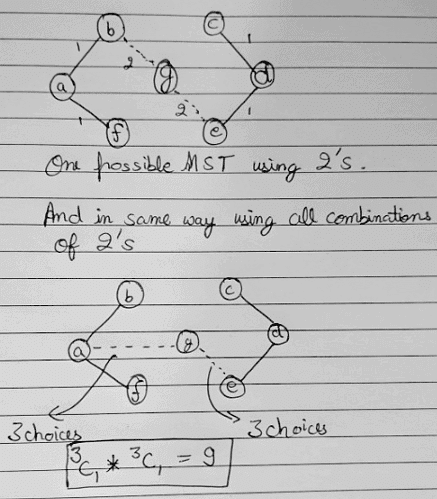
Q2: Let G be an undirected connected graph in which every edge has a positive integer weight. Suppose that every spanning tree in G has even weight. Which of the following statements is/are TRUE for every such graph G? (2024 SET-2)
(a) All edges in G have even weight
(b) All edges in G have even weight OR all edges in G have odd weight
(c) In each cycle G in G, all edges in G have even weight
(d) In each cycle G in G, either all edges in G have even weight OR all edges in G have odd weight
Ans: (d)
Sol:
Given:
- Graph G is undirected and connected.
- Every edge in G has a positive integer weight.
- Every spanning tree in G has an even weight.
Now, let's analyze each statement again in the context of these conditions:
Statement (a): All edges in G have even weight.
- This statement is false. The condition that every spanning tree has even weight does not enforce that each individual edge in the graph has even weight. It only ensures that the sum of weights of any spanning tree is even, not necessarily each edge.
Statement (b): All edges in G have even weight OR all edges in G have odd weight.
- This statement is true. The reason is that the total weight of any spanning tree, being even, implies that the parity (even or odd) of the weights of all edges in the graph must be consistent. If every spanning tree has even weight, then all edges in the graph must collectively have either all even weights or all odd weights to maintain this property across all possible spanning trees.
Statement (c): In each cycle in G, all edges have even weight.
- This statement is false. A cycle in G could contain edges with both even and odd weights. The condition that every spanning tree has even weight does not impose any restriction on the parity of edge weights within cycles that are not part of spanning trees.
Statement (d): In each cycle in G, either all edges have even weight OR all edges have odd weight.
- This statement is true. The key insight here is derived from the properties of spanning trees. Since every spanning tree has an even weight, any cycle in G that is not part of a spanning tree must have a consistent parity of edge weights. If there were a cycle with edges of mixed parity (some even, some odd), combining this cycle with a spanning tree (which has even weight) would result in a spanning tree with an odd weight, which contradicts the given condition.
Conclusion:
- The correct answer is option (d): "In each cycle in G, either all edges have even weight OR all edges have odd weight."
This conclusion follows logically from the given condition about spanning trees and the implications for cycles within the graph G. It shows that the parity of edge weights in any cycle must be uniform (either all even or all odd) to ensure that every spanning tree in G has an even weight.
Q3: The number of spanning trees in a complete graph of 4 vertices labelled A, B, C, and D is __________. (2024 SET-1)
(a) 12
(b) 16
(c) 18
(d) 22
Ans: (b)
Sol: Number of spanning trees in any complete graph (Kn) is nn-2, where n is a number of vertices.
here n = 4 ∴ the number of spanning tree is 44-2 = 42 = 16
So the correct answer is 16.
Q4: Let G(V, E) be a directed graph, where V = {1, 2, 3, 4, 5} is the set of vertices and E is the set of directed edges, as defined by the following adjacency matrix A.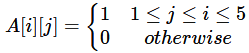
A[i][j] = l indicates a directed edge from node i to node j. A directed spanning tree of G, rooted at r ∈ V, is defined as a subgraph T of G such that the undirected version of T is a tree, and T contains a directed path from r to every other vertex in V. The number of such directed spanning trees rooted at vertex 5 is _________ (2022)
(a) 24
(b) 36
(c) 12
(d) 6
Ans: (a)
Sol:
Method 1(Complete Analysis):
Directed Spanning Tree definition is given. From the definition, it can be seen that Directed Spanning Tree(DST) is basically a Directed Acyclic Graph (DAG) whose root node is 5, and it contains all the vertices. We need to find how many such DAGs are possible. Let's find out :
5 is the root node of the DAG. Let's fix this at one place and permute all other numbers.
5, 4, 3, 1, 2 is one permutation possible, Similarly 5, 3, 4, 1, 2 is other permutation possible.
Total there are 4! = 24 permutations possible.
Now you give me any permutation (where 5 is fixed at start) and I will give you corresponding DAG.
For example, you give me 5, 3, 4, 1, 2 as permutation then i will draw following DAG.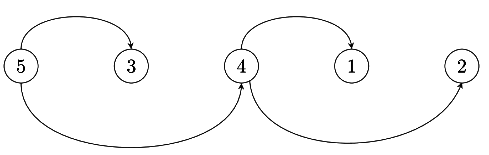
For 3, nearest larger node on the left is 5.
For 4, nearest larger node on the left is 5.
For 1, nearest larger node on the left is 4.
For 2, nearest larger node on the left is 4.
In this way, we can say that for every permutation there is unique DAG.
Now, we can say number of DAGs is atleast as large as number of permutations. Maybe more DAGs than 4!
Can we have unique permutation for any given DAG? - if yes then there is bijection between set of DAGS possible and the set of permutations possible, And So answer will be 4!.
Before that first understand that these 2 DAGs are the same-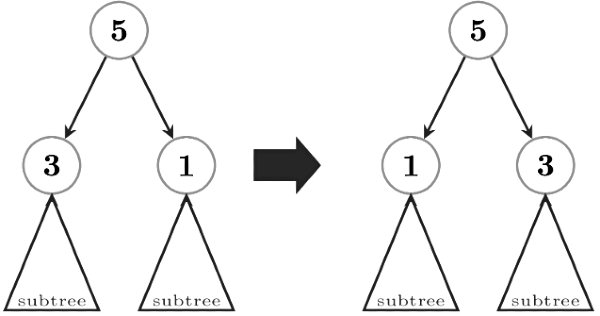
it does not matter if you swap left or right subtrees because they (Question makers) are interested in subgraphs and both the DAGs above are the same subgraph.
Now you give me a DAG, I will arrange all siblings of a node in increasing order(from left to right) and then
I will take level order traversal to write permutation. For example, You give me the following DAG -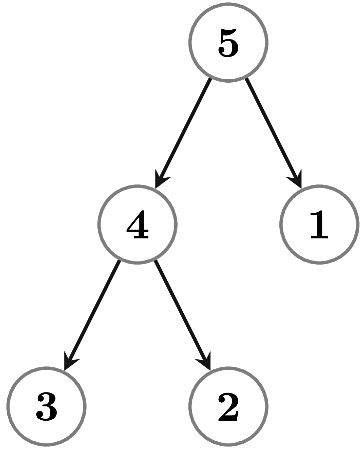
I will rearrange nodes as following –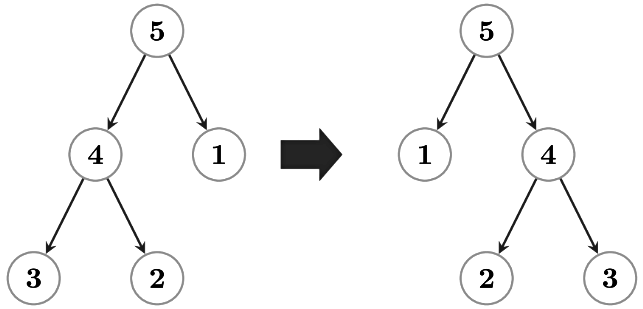
Level order will be 5, 1, 4, 2, 3
Now if we try to draw a DAG using same permutation, you will find same DAG.
For 1, nearest larger node on the left is 5.
For 4, nearest larger node on the left is 5.
For 2, nearest larger node on the left is 4.
For 3, nearest larger node on the left is 4.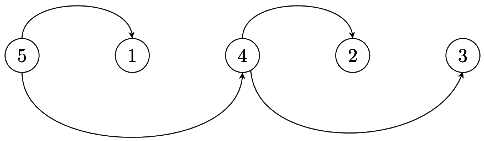
Both DAGs are the same.
Now it does not matter how I am converting a DAG to permutation or permutation to DAG. Consider my method as blackbox, I have some definite rule as black box and I can convert to each other uniquely.
So, we have shown that There is a bijection between set of DAGs possible and the set of permutations possible, Hence, answer will be 4!.
Q5: Consider a simple undirected weighted graph G, all of whose edge weights are distinct. Which of the following statements about the minimum spanning trees of G is/are TRUE? (2022)
(a) The edge with the second smallest weight is always part of any minimum spanning tree of G.
(b) One or both of the edges with the third smallest and the fourth smallest weights are part of any minimum spanning tree of G.
(c) Suppose S ⊆ V be such that S ≠ ∅ and S ≠ V. Consider the edge with the minimum weight such that one of its vertices is in S and the other in V \ S. Such an edge will always be part of any minimum spanning tree of G.
(d) G can have multiple minimum spanning trees.
Ans: (a, b and c)
Sol: In the given undirected weighted graph, All the edge weights are distinct, hence, there will be Exactly One Minimum Spanning Tree for the graph.
Option A:
The edge with the second smallest weight is always part of any minimum spanning tree of G.
Since G has Exactly One MST, the above statement can be written as "The edge with the second smallest weight is always part of the minimum spanning tree of G."
This can be proven by "Kruskal Algorithm" to find MST. Minimum Edge, Second Minimum Edge, both will be added in the MST by Kruskal Algorithm (Two edges cannot bring cycle)
Option B:
One or both of the edges with the third smallest and the fourth smallest weights are part of any minimum spanning tree of G.
Since G has Exactly One MST, the above statement can be written as "One or both of the edges with the third smallest and the fourth smallest weights are part of the minimum spanning tree of G."
This is True. Minimum Edge, Second Minimum Edge, both will be added in the MST by Kruskal Algorithm (Two edges cannot bring cycle), BUT third minimum edge might introduce cycle in the MST, and if so happens, we do not include third minimum edge in the MST and add fourth minimum edge in the MST.
Option D:
G can have multiple minimum spanning trees: False (Because all edge weights are distinct)
Option C:
Suppose S ⊆ V be such that S ≠ ∅ and S ≠ V. Consider the edge with the minimum weight such that one of its vertices is in S and the other in V - S. Such an edge will always be part of any minimum spanning tree of G.
This is True. This is a popular and basic property of Minimum Spanning Tree, known as "Cut Property." The cut property is the basis for the algorithms that we consider for the MST problem. "Cut Property" and "Cycle Property" are basic theorems in the study of MST, and must be understood by all, with proof.
Cut property:
Given any cut in an edge-weighted graph (with all edge weights distinct), the crossing edge of minimum weight is in the MST of the graph.
Given a cut (S, V - S) of G, recall that an edge (u, v) ∈ E is said to cross the cut if exactly one of u and v is in S. An edge e = (u, v) is a minimum weight edge crossing the cut (S, V - S) if its weight is the smallest of any edge crossing (S, V - S).
Then e = (u, v) must be included in the minimum spanning trees of G.
Let G = (V, E, w) be a connected undirected weighted graph with distinct edge weights. For any cut (U, V - U) of G, the minimum weight edge that crosses the cut is in the minimum spanning tree MST(G) of G.
We can prove it as following:
Proof :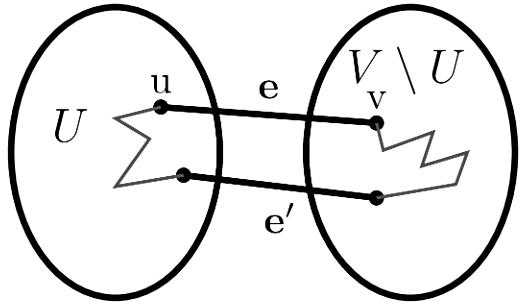
The proof is by contradiction. Assume the minimum-weighted edge e = (u, v) is not in the MST. Since the MST spans the graph and is a connected tree, there must be a unique simple path P connecting u and v in the MST (i.e., consisting of just edges in the MST). The path must cross the cut between U and V - U at least once since u and v are on opposite sides. Let e' be an edge in P that crosses the cut. By assumption the weight of e' is larger than that of e. Now, insert e into the graph-this gives us a cycle that includes both e and e' and remove e' from the graph to break the only cycle and obtain a spanning tree again. Now, since the weight of e is less than that of e', the resulting spanning tree has a smaller weight. This is a contradiction and thus e must have been in the tree.
Hence Proved.
Q6: Let G be a connected undirected weighted graph. Consider the following two statements.
S1: There exists a minimum weight edge in G which is present in every minimum spanning tree of G.
S2: If every edge in G has distinct weight, then G has a unique minimum spanning tree.
Which one of the following options is correct? (2021 SET-2)
(a) Both S1 and S2 are true
(b) S1 is true and S2 is false
(c) S1 is false and S2 is true
(d) Both S1 and S2 are false
Ans: (c)
Sol: We can think of running the Kruskals algorithm for finding the Minimum Spanning Tree on graph G.
While doing that, we sort the edges based on their weight and start selecting edges from the smallest weight
(Wsmall for example).
Problem with S1: If we have multiple copies of Wsmall, then a specific Wsmall weighted edge is not guaranteed to be selected by Kruskals algorithm.
S2 is Correct: If the sorted order of the edges contains only distinct values, Kruskals algorithm will always select a unique set of edges resulting in a unique minimum spanning tree.
Correct option: C.
Q7: Consider the following undirected graph with edge weights as shown: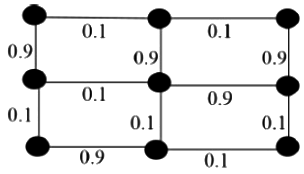
The number of minimum-weight spanning trees of the graph is __________ (2021 SET-1)
(a) 4
(b) 6
(c) 5
(d) 3
Ans: (d)
Sol: For finding a minimum-weight spanning tree we have different algorithms like the Prim, Kruskal's algorithm.
A spanning tree means a sub-graph of the original graph that should be the tree and connected to all the vertices together.
A Minimum spanning tree is for a weighted, connected and undirected graph is a spanning tree with weight less than or equal to the weight of every other spanning tree. The weight of a spanning tree is the sum of the weights of each edge of the spanning tree.
Now to find out MST of the given graph using Kruskal's algorithm (we can use any method here) we can follow the 2 step process:
- Sort all the edges in increasing order of their weight.
- Select the smallest edge & check if it forms a cycle with the spanning tree formed so far. If a cycle is not formed, include this edge. Else, discard it.
After applying the above steps graph will look like this: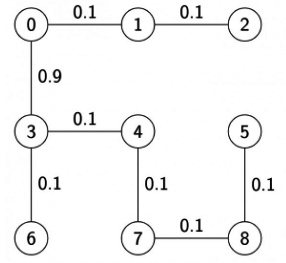
In the above figure, we cannot add edges (6, 7) or (4, 5) because it creates a cycle in MST. So we have only 3 edges remaining which are (0, 3), (1, 4) and (2, 5).
Since we know that for n vertices, the number of edges should be (n - 1) in MST. so from 3 edges we can select only 1 edge that is:(3/1) = 3 ways.
- 1st MST
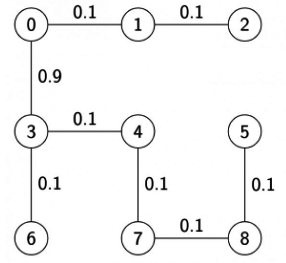
- 2nd MST
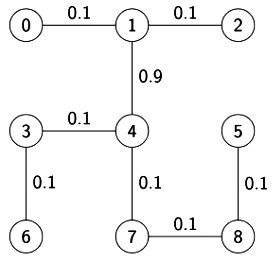
- 3rd MST
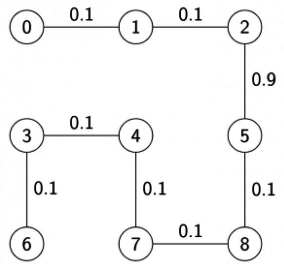
∴ Total 3 MSTs are possible for the given graph.
Q8: Consider a graph G = (V, E), where V = {v1, v2, ..., v100}, E = {(vi, vj)|1 ≤ i < j ≤ 100}, and weight of the edge (vi, vj) is i - j]. The weight of minimum spanning tree of G is ________ (2020)
(a) 100
(b) 99
(c) 199
(d) 90
Ans: (b)
Sol: Vertices are given from 1 to 100 and edge weight between the vertices is absolute values of the difference between the suffix values of the vertices.
So, if we choose the vertices consecutively as 1 - 2 - 3 - 4 - 5 - ... - 99 - 100 we get the spanning tree with minimum weight.
Spanning tree will contain 99 edges since there are 100 vertices and cost of each edge is '1'.
Therefore, weight of spanning tree would be 99 x 1 = 99.
Q9: Let G = (V, E) be a weighted undirected graph and let T be a Minimum Spanning Tree (MST) of G maintained using adjacency lists. Suppose a new weighed edge (u, v) ∈ V x V is added to G. The worst case time complexity of determining if T is still an MST of the resultant graph is (2020).
(a) Θ( |E| + |V|)
(b) Θ(|E| |V|)
(c) Θ(|E| log |V|)
(d) Θ(|V|)
Ans: (d)
Sol: We can do this in O(IVI) in the following way:
- Run BFS in T from u to v to detect the edge with maximum value in that path. -O(|V|).
- If the weight of that edge is greater than the weight of the edge you're trying to add, remove that old edge and add the new one.
- Otherwise, do nothing, because the new edge would not improve the MST. -O(1).
The rationale behind this solution is that simply adding an edge into T would create exactly one cycle, and to restore the MST property we have to remove the edge with maximum value from that cycle.
Q10: Let G be any connection, weighted, undirected graph:
I. G has a unique minimum spanning tree if no two edges of G have the same weight.
II. G has a unique minimum spanning tree if, for every cut of G, there is a unique minimum weight edge crossing the cut.
Which of the above two statements is/are TRUE? (2019)
(a) I only
(b) II only
(c) Both I and II
(d) Neither I nor II
Ans: (c)
Sol: 1. If edge weights are distinct then there exist unique MST.
2. If for every cut of a graph there is a unique light edge crossing the cut then the graph has a unique minimum spanning tree but converse may not be true.
Proof by contradiction:
Lemma: If an edge e is contained in some minimum spanning tree, then it is a minimum cost edge crossing some cut of the graph.
Assume MST is not unique and there exist two MST's T1 and T2
Suppose e1 ∈T1 but e1 ∉ T2, if we remove e1 from T1, then we will have disconnected graph with two set of vertices V1 and V2. According to lemma e1 is a minimum cost edge in the cut between V1 and V2.
Suppose e2 ∈ T2 but e2 ∉ T1, if we remove e2 from T2, then we will have disconnected graph with two set of vertices V1 and V2. According to lemma e2 is a minimum cost edge in the cut between V1 and V2.
Because the minimum cost edge is unique implies e1 and e2 is the same edge. e1 ∈ T2 and e2 ∈ T1. We have chosen e1 at random, of all edges in T1, also in T2 and same for e2. As a result, the MST is unique.
So both statements in the question are TRUE.
Answer is (C).
Q11: Consider the following undirected graph G: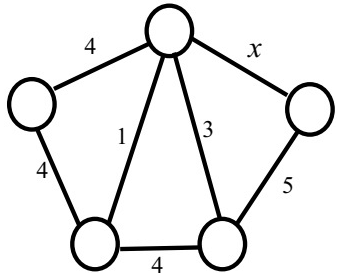
Choose a value for x that will maximize the number of minimum weight spanning trees (MWSTs) of G. The number of MWSTs of G for this value of x is _______. (2018)
(a) 3
(b) 4
(c) 5
(d) 1
Ans: (b)
Sol: Number of possible MSTs increase, when we have multiple edges with same edge weights.
To maximize the number of MST, x should be 5.
In the question, number of MST is asked for the value of X.
So, number of MST = 2 x 2 = 4 (Answer)
(Because one 4 forms cycle, cant be included in any way. Now from two 4 and 5 we can select one in 2 x 2 = 4 ways)
Q12: Let G = (V, E) be any connected undirected edge-weighted graph. The weights of the edges in E are positive and distinct. Consider the following statements:
(I) Minimum spanning tree of G is always unique.
(II) Shortest path between any two vertices of G is always unique.
Which of the above statements is/are necessarily true? (2017 SET-1)
(a) (I) only
(b) (II) only
(c) Both (I) and (II)
(d) Neither (1) nor (II)
Ans: (a)
Sol: MST is not unique only when edges are not distinct. Here the edges are distinct. Be careful for the keyword DISTINCT.
Shortest Path can be different even if the edges are distinct. Example is shown below. Shortest path from A to C is not unique here.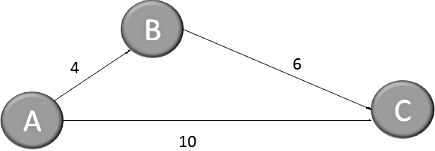
Q13: G = (V,E) is an undirected simple graph in which each edge has a distinct weight, and e is a particular edge of G. Which of the following statements about the minimum spanning trees (MSTs) of G is/are TRUE?
I. If e is the lightest edge of some cycle in G, then every MST of G includes e
II. If e is the heaviest edge of some cycle in G, then every MST of G excludes e (2016 SET-1)
(a) I only
(b) II only
(c) both I and II
(d) neither I nor II
Ans: (b)
Sol:
Statement 1:- False by [Cut Property of MST]
See counter example :- Here in below Graph G in (cycle 3, 4, 5) 3 is the lightest edge and still it is not included in MST.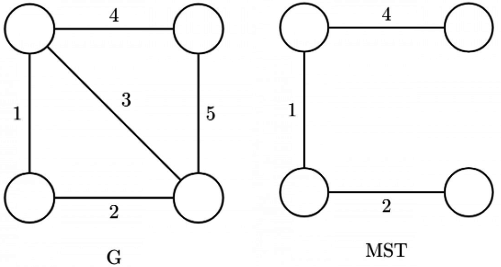
Statement 2:- True by [ Cycle property of MST]: (in above Graph G 1 - 2 - 3 is a cycle and 3 is the heaviest edge) If heaviest edge is in cycle then we will always exclude that because cycle is there means, we can have other choice of low cost edges. (If edge weights are not distinct even the heaviest edge can be part of the MST and here in question distinct edge weight is clearly mentioned)
So, option B is answer.
Q14: Let G be a complete undirected graph on 4 vertices, having 6 edges with weights being 1,2,3,4,5, and 6. The maximum possible weight that a minimum weight spanning tree of G can have is. (2016 SET-1)
(a) 6
(b) 7
(c) 8
(d) 5
Ans: (b)
Sol: Many people here have not understood the question itself. Consider a complete graph of 4 vertices. We have a total of 6 edges of given weights but we do not have the exact graph. Many different graphs are possible each having a different structure. Consider these 2 graphs, both of them are different. We do not know the exact structure of the graph, so what the question wants is to find the MST of all such structures and out of these tell the weight of the MST having maximum weight. The point about the MST of a graph with unique edge weights is valid for a given structure of the graph. With the same set of edge weights more than 1 graph is possible and all of them can have different MSTs.
My solution: Draw a complete graph of 4 vertices. Sort given edges y weight in increasing order. Just like Kruskal's algorithm sort the edges by weight. MST of graph with 4 vertices and 6 edges will have 3 edges. Now in any case we will have to include edges with weights 1 and 2 as they are minimum and Kruskal's algorithm includes minimum weight edge if it does not form a cycle. We can not have a cycle with 2 edges. In Kruskal's algorithm, an edge will be rejected if it forms a cycle with the edges already selected. To increase the weight of our MST we will try to reject the edge with weight 3. This can be done by forming a cycle. The graph in pic1 shows this case. This implies, the total weight of this graph will be 1 + 2 + 4 = 7.
Q15: Let G be a weighted connected undirected graph with distinct positive edge weights. If every edge weight is increased by the same value, then which of the following statements is/are TRUE?
P: Minimum spanning tree of G does not change
Q: Shortest path between any pair of vertices does not change (2016 SET-1)
(a) P only
(b) Q only
(c) Neither P nor Q
(d) Both P and Q
Ans: (a)
Sol: Statement P is true.
For statement Q consider a simple graph with 3 nodes.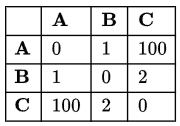
Shortest path from A to C is A-B-C = 1 + 2 = 3
Now if the value of each edge is increased by 100,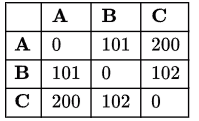
The shortest path from A to C is A-C = 200, (A-B-C = 101 + 102 = 203)
Hence, option A is correct.
Q16: The number of spanning trees for a complete graph with seven vertices is (2015)
(a) 25
(b) 75
(c) 35
(d) 22x5
Ans: (b)
Sol: No of spanning tree possible in complete graph with n node=nn-2
So No of spanning tree possible in complete graph with 7 node=75
Q17: Let G be a connected undirected graph of 100 vertices and 300 edges. The weight of a minimum spanning tree of G is 500. When the weight of each edge of G is increased by five, the weight of a minimum spanning tree becomes __________. (2015SET-3)
(a) 500
(b) 995
(c) 2500
(d) 1000
Ans: (b)
Sol: First find no of edges in mst.
Mst has n 1 edges where n is no of vertices. 100 - 1 = 99 edges
Each 99 edges in mst increases by 5 so weight in mst increased 99 x 5 = 495
Now total weight of mst = 500 + 495 = 995
Q 18: The graph shown below has 8 edges with distinct integer edge weights. The minimum spanning tree (MST) is of weight 36 and contains the edges: {(A, C), (B, C), (B, E), (E, F), (D, F)}. The edge weights of only those edges which are in the MST are given in the figure shown below. The minimum possible sum of weights of all 8 edges of this graph is _________. (2015 SET-1)
(a) 66
(b) 69
(c) 72
(d) 75
Ans: (b)
Sol: Consider the cycle ABC. AC and BC are part of minimum spanning tree. So, AB should be greater than max (AC, BC) (greater and not equal as edge weights are given to be distinct), as otherwise we could add AB to the minimum spanning tree and removed the greater of AC, BC and we could have got another minimum spanning tree. So, AB > 9.
Similarly, for the cycle DEF, ED > 6.
And for the cycle BCDE, CD > 15.
So, minimum possible sum of these will be 10 + 7 + 16 = 33. Adding the weight of spanning tree, we get the total sum of edge weights
= 33 + 36 = 69
Q19: The number of distinct minimum spanning trees for the weighted graph below is (2014 SET-2)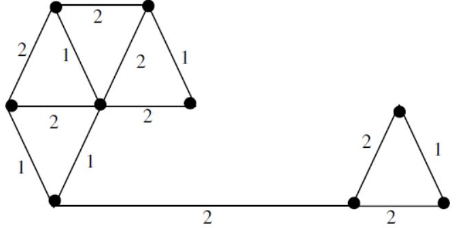
(a) 4
(b) 5
(c) 6
(d) 7
Ans: (c)
Sol: 6 is the answer.
2 x 3 = 6 possibilities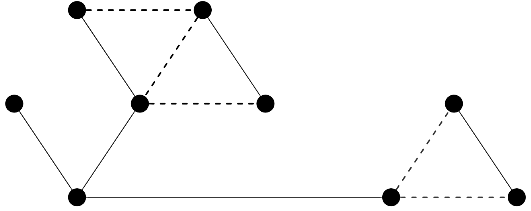
Q20: Let G be a weighted graph with edge weights greater than one and G' be the graph constructed by squaring the weights of edges in G. Let T and T' be the minimum spanning trees of G and G', respectively, with total weights t and t'.
Which of the following statements is TRUE? (2012)
(a) T' = T with total weight t' = t2
(b) T' = T with total weight t' < t2
(c) T' ≠ T but total weight t' = t2
(d) None of the above
Ans: (d)
Sol: When the edge weights are squared the minimum spanning tree won't change. t' < t2, because sum of squares is always less than the square of the sums except for a single element case.
Hence, B is the general answer and A is also true for a single edge graph. Hence, in GATE 2012, marks were given to all.
Q21: An undirected graph G(V, E) contains n (n>2) nodes named v1, v2.....vn. Two nodes vi, vj are connected if and only if 0<|i-j|≤2. Each edge (vi, vj) is assigned a weight i + j. A sample graph with n=4 is shown below.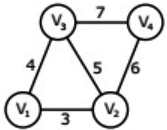
The length of the path from v5 to v6 in the MST of previous question with n = 10 is (2011)
(a) 11
(b) 25
(c) 31
(d) 41
Ans: (c)
Sol: 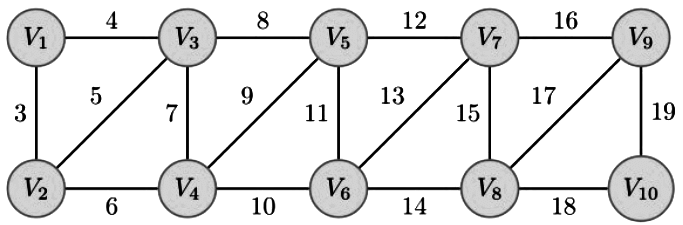
Above is the graph.
Below is the MST.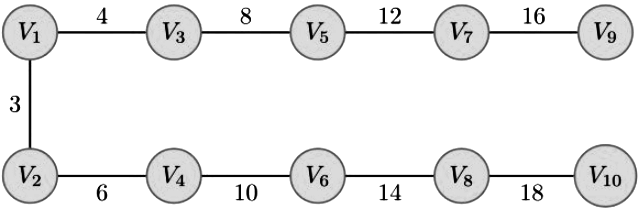
Length of the path from vs to v6 = 8 + 4 + 3 + 6 + 10 = 31 (Answer)
Correct Answer: C
Q22: An undirected graph G(V, E) contains n (n>2) nodes named v1, v2.....vn. Two nodes vi, vj are connected if and only if 0<|i-j|≤2. Each edge (vi, vj) is assigned a weight i + j. A sample graph with n=4 is shown below.
What will be the cost of the minimum spanning tree (MST) of such a graph with n nodes? (2011)
(a) 1/12(11n2 - 5n)
(b) n2 - n + 1
(c) 6n-11
(d) 2n+1
Ans: (b)
Sol: We observe a pattern in the weight of MST being formed
For n = 3 (1 + 2 + 3) + (1)
For n = 4 (1 + 2 + 3 + 4) + (1 + 2)
For n = 5 (1 + 2 + 3 + 4 + 5) + (1 + 2 + 3)
These can be obtained by drawing graphs for these graphs.
∴ Total weight of MST is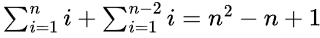
Q23: Consider a complete undirected graph with vertex set {0, 1, 2, 3, 4}.
Entry Wij in the matrix W below is the weight of the edge {i, j}.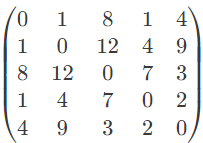
What is the minimum possible weight of a spanning tree T in this graph such that vertex 0 is a leaf node in the tree T? (2010)
(a) 7
(b) 8
(c) 9
(d) 10
Ans: (d)
Sol: 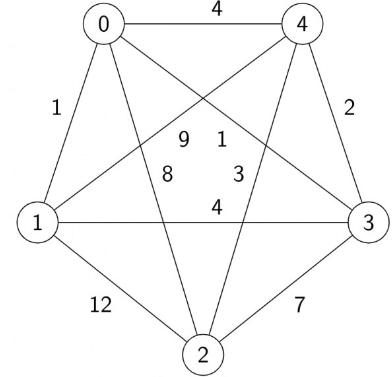
Answer is (D) 10. The edges of the spanning tree are: 0 - 1,1 - 3,3 - 4,4 - 2. Total Weight = 10
Q24: Consider the following graph: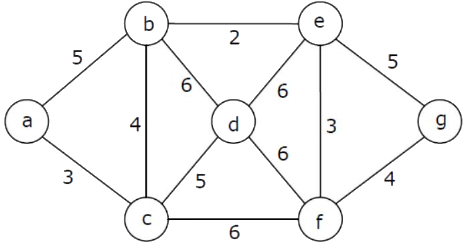
Which one of the following is NOT the sequence of edges added to the minimum spanning tree using Kruskal's algorithm? (2009)
(a) (b, e) (e, f) (a, c) (b, c) (f, g) (c, d)
(b) (b, e) (e, f) (a, c) (f, g) (b, c) (c, d)
(c) (b, e) (a, c) (e, f) (b, c) (f, g) (c, d)
(d) (b, e) (e, f) (b, c) (a, c) (f, g) (c, d)
Ans: (d)
Sol: In Option D b-c with weight, 4 is added before a-c with weight 3 is added. In Kruskal's algorithm, edges should be added in non-decreasing order of weight.
So, Option D may be correct.
Q25: For the undirected, weighted graph given below, which of the following sequences of edges represents a correct execution of Prim's algorithm to construct a Minimum Spanning Tree? (2008)
(a) (a, b), (d, f), (f, c), (g, i), (d, a), (g, h), (c, e), (f, h)
(b) (c, e), (c, f), (f, d), (d, a), (a, b), (g, h), (h, f), (g, i)
(c) (d, f), (f, c), (d, a), (a, b), (c, e), (f, h), (g, h), (g, i)
(d) (h, g), (g, i), (h, f), (f, c), (f, d), (d, a), (a, b), (c, e)
Ans: (c)
Sol: Prim's algorithm starts with from any vertex and expands the MST by adding one vertex in each step which close to the Intermediate MST(made till previous step).
Therefore, correct answer would be (C).
(A): (d, f) is chosen but neither d nor f vertices are part of the previous MST(MST made till previous step).
(B): (g, h) is chosen but neither g or h vertices are part of the previous MST(MST made till previous step).
(D): (f, c) is chosen but at that point (f, d) is close to the intermediate MST.
Q26: G is a graph on n vertices and 2n-2 edges. The edges of G can be partitioned into two edge-disjoint spanning trees. Which of the following is NOT true for G? (2008)
(a) For every subset of k vertices, the induced subgraph has at most 2k-2 edges
(b) The minimum cut in G has at least two edges
(c) There are two edge-disjoint paths between every pair of vertices
(d) There are two vertex-disjoint paths between every pair of vertices
Ans: (d)
Sol: There are 2 spanning trees (a spanning tree connects all n vertices) for G which are edge disjoint. A spanning tree for n nodes require n - 1 edges and so 2 edge-disjoint spanning trees requires 2n - 2 edges.
As G has only 2n - 2 edges, it is clear that it doesn't have any edge outside that of the two spanning trees.
Now lets see the cases:
Lets take any subgraph of G with k vertices. The remaining subgraph will have n - k vertices. Between these two subgraphs (provided both has at least one vertex) there should be at least 2 edges, as we have 2 spanning trees in G. So, (B) is TRUE. Also, in the subgraph with k vertices, we cannot have more than 2k - 2 edges as this would mean that in the other subgraph with n - k vertices, we would have less than 2n - 2k edges, making 2 spanning trees impossible in it. So, (A) is also TRUE.
A spanning tree covers all the vertices. So, 2 edge-disjoint spanning trees in G means, between every pair of vertices in G we have two edge-disjoint paths (length of paths may vary). So, (C) is also TRUE.
So, that leaves option (D) as answer. It is not quite hard to give a counter example for (D).
Q27: What is the largest integer m such that every simple connected graph with n vertices and n edges contains at least m different spanning trees? (2007)
(a) 1
(b) 2
(c) 3
(d) n
Ans: (c)
Sol: Option (C) is Correct, reason is as follows:
A graph is connected and has 'n' vertices and edges means, exactly one cycle is there.
Now we can make a different spanning tree by removing one edge from the cycle, one at a time.
Minimum cycle length can be 3, So, there must be at least 3 spanning trees in any such graph.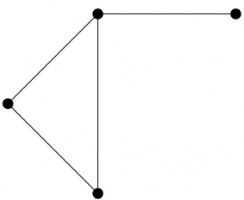
Consider the above graph. Here n = 4 and three spanning trees possible at max (removing edges of cycle one at a time, alternatively).
So, any such Graph with minimum cycle length '3' will have at least 3 spanning trees.
Q28: Let w be the minimum weight among all edge weights in an undirected connected graph. Let e be a specific edge of weight w. Which of the following is FALSE? (2007)
(a) There is a minimum spanning tree containing e.
(b) If e is not in a minimum spanning tree T, then in the cycle formed by adding e to T, all edges have the same weight.
(c) Every minimum spanning tree has an edge of weight w.
(d) e is present in every minimum spanning tree.
Ans: (d)
Sol: A minimum spanning tree must have the edge with the smallest weight (In Kruskal's algorithm we start from the smallest weight edge). So, C is TRUE.
If e is not part of a minimum spanning tree, then all edges which are part of a cycle with e, must have weight ≤ e, as otherwise we can interchange that edge with e and get another minimum spanning tree of lower weight. So, B and A are also TRUE.
D is false because, suppose a cycle is there with all edges having the same minimum weight w. Now, any one of them can be avoided in any minimum spanning tree.
Q29: Consider the following graph: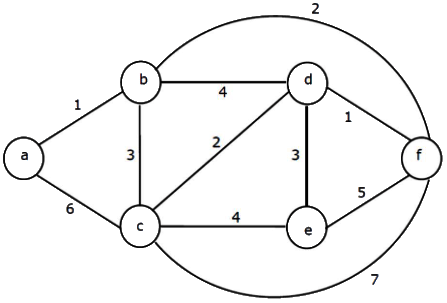
Which one of the following cannot be the sequence of edges added, in that order, to a minimum spanning tree using Kruskal's algorithm? (2006)
(a) (a - b),(d - f),(b - f),( d - c),(d - e)
(b) (a - b),(d - f),(d - c),(b - f),(d - e)
(c) (d - f),(a - b),(d - c),(b - f),(d - e)
(d) (d - f),(a - b),(b - f),(d - e),(d - c)
Ans: (d)
Sol: In Kruskal's algo the edges are added in non decreasing order of their weight. But in Option D edge d - e with weight 3 is added before edge d - c with weight 2.
Correct Answer: D
Q30: Consider a weighted complete graph G on the vertex set {U1, U2, ..., Un} such that the weight of the edge (vi, vj) is 2|i-j|. The weight of a minimum spanning tree (2006)
(a) n-1
(b) 2n-2
(c) (n/2)
(d) n2
Ans: (b)
Sol: 2(n - 1) the spanning tree will traverse adjacent edges since they contain the least weight.
Q31: Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE? (2005)
(a) There exists a cutset in G having all edges of maximum weight.
(b) There exists a cycle in G having all edges of maximum weight.
(c) Edge e cannot be contained in a cycle.
(d) All edges in G have the same weight
Ans: (a)
Sol: Option A is correct.
Questions says the MST of graph G contain an edge e which is a maximum weight edge in G. Need to choose the answer which is always true to follow the above constraint.
Case 1:
Option B says that if edge e is in MST then for sure there is a cycle having all edges of maximum weight. But it is not true always because when there is only n-1 edges(but no cycle) in graph then also maximum edge has to be taken for MST.
Case 2:
Option C says otherwise. That if e is in MST then it cannot be in any cycle that is wrong as if there is a cycle with all maximum edges then also e will be in MST
Option D says all edges should be of same weight same explanation if there are n 1 distinct edges(but no cycle) in G then have to take all edges including maximum weight edge.
And at last option A says if e is in MST then for sure there is a cut-set (A subset of Edge set of G whose removal disconnects the graph) in G having all edges of maximum weight. And it is true.
Because then only we maximum weight edges has to be taken in MST.
For eg. If there are n - 1 edges (but no cycle) then if edge e is not taken in the MST then MST will not be connected.
Q32: Let s and t be two vertices in a undirected graph G = (V, E) having distinct positive edge weights. Let [X, Y] be a partition of V such that S ∈ X and t ∈ Y. Consider the edge e having the minimum weight amongst all those edges that have one vertex in X and one vertex in Y.
Let the weight of an edge e denote the congestion on that edge. The congestion on a path is defined to be the maximum of the congestions on the edges of the path. We wish to find the path from s to t having minimum congestion. Which one of the following paths is always such a path of minimum congestion? (2005)
(a) a path from s to t in the minimum weighted spanning tree
(b) a weighted shortest path from s to t
(c) an Euler walk from s to t
(d) a Hamiltonian path from s to t
Ans: (a)
Sol: Here answer should be A.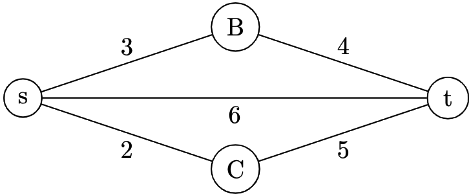
Here, shortest path will give 6.
Spanning tree contains edges of weights 2,3,4 so congestion in this case is max (2, 3, 4), that is,4. For path s to t, overall congestion is max(3, 4) = 4 but total weight is 7.
Option C and D are I think not related to this question.
Q33: Let s and t be two vertices in a undirected graph G = (V, E) having distinct positive edge weights. Let [X, Y] be a partition of V such that s ∈ X and t ∈ Y. Consider the edge e having the minimum weight amongst all those edges that have one vertex in X and one vertex in Y. (2005)
The edge e must definitely belong to:
(a) the minimum weighted spanning tree of G
(b) the weighted shortest path from s to t
(c) each path from s to t
(d) the weighted longest path from s to t
Ans: (a)
Sol: The answer should be Option A because edge e is the lightest safe edge connecting X and Y so the minimum spanning tree of G must contain e (Greedy and optimal choice). While option (B) might seem correct but it is not always true. One such case is when G is not connected therefore there might not be any path between s and t.
Since the question is about definitely TRUE, (B) is incorrect and (A) is the only correct option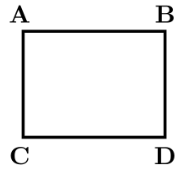
Lets say AC = 1, CD = 2,BD = 3 and AB = 4
Then if s = A and t = B then AC is the lightest edge crossing X and Y where X = A and Y = C, B, D
But clearly AC is not on the shortest path from A to B. The shortest path is AB = 4.
Q34: An undirected graph G has n nodes. Its adjacency matrix is given by an nxn square matrix whose
(i) diagonal elements are 0's and
(ii) non-diagonal elements are 1's.
which one of the following is TRUE? (2005)
(a) Graph G has no minimum spanning tree (MST)
(b) Graph G has a unique MST of cost n-1
(c) Graph G has multiple distinct MSTs, each of cost n-1
(d) Graph G has multiple spanning trees of different costs
Ans: (c)
Sol: Graph G has multiple distinct MSTs, each of cost n - 1
From the given data given graph is a complete graph with all edge weights 1. A MST will contain n 1 edges.
Hence weight of MST is n - 1.
The graph will have multiple MST. In fact all spanning trees of the given graph will be MSTs also since all edge weights are equal.
Q35: Consider the undirected graph below: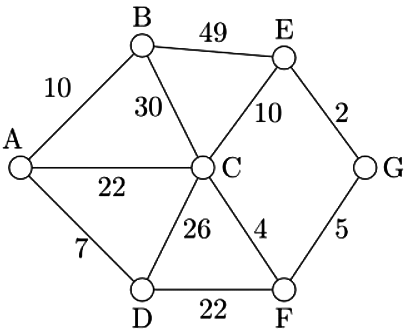
Using Prim's algorithm to construct a minimum spanning tree starting with node A, which one of the following sequences of edges represents a possible order in which the edges would be added to construct the minimum spanning tree? (2004)
(a) (E, G), (C, F), (F, G), (A, D), (A, B), (A, C)
(b) (A, D), (A, B), (A, C), (C, F), (G, E), (F, G)
(c) (A, B), (A, D), (D, F), (F, G), (G, E), (F, C)
(d) (A, D), (A, B), (D, F), (F, C), (F, G), (G, E)
Ans: (d)
Sol: A and B produce disconnected components with the Given order in options which is Never allowed by prims's algorithm.
C produces connected component every instant a new edge is added but when first vertex is chosen (first vertex is chosen randomly) first edge must be the minimum weight edge that is chosen. Therefore, (A, D) must be chosen Before (A, B). Therefore, C is FALSE.
Q36: What is the weight of a minimum spanning tree of the following graph? (2003)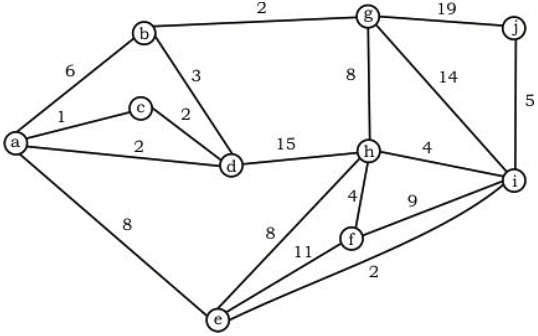
(a) 29
(b) 31
(c) 38
(d) 41
Ans: (b)
Sol: Apply Prim's algorithm, start from A as shown in figure below.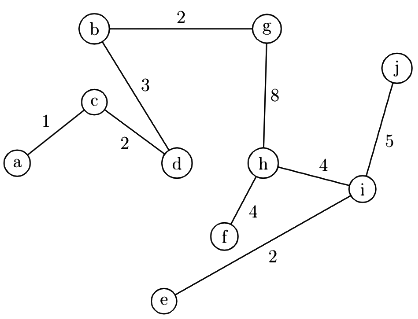
Add all the weights in the given figure which will be equal to 31.
Correct Answer: B
Q37: Let G be an undirected connected graph with distinct edge weights. Let emax be the edge with maximum weight and emin the edge with minimum weight. Which of the following statements is false? (2000)
(a) Every minimum spanning tree of G must contain emin
(b) If emaz is in a minimum spanning tree, then its removal must disconnect G
(c) No minimum spanning tree contains emax
(d) G has a unique minimum spanning tree
Ans: (c)
Sol: C the case should be written as "may or may not", to be true.
D will always be true as per the question saying that the graph has distinct weights.
Correct Answer: C
Q38: The correct matching for the following pairs is (1997)
(a) A-2 B-4 C-1 D-3
(b) A-3 B-4 C-1 D-2
(c) A-3 B-4 C-2 D-1
(d) A-4 B-1 C-2 D-3
Ans: (b)
Sol: Answer : (B) A-3 B-4 C-1 D-2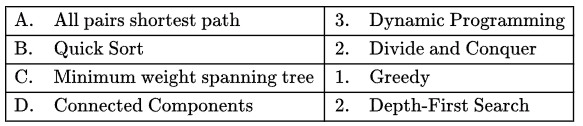
Q39: Choose the correct alternatives (more than one may be correct) and write the corresponding letters only:
Kruskal's algorithm for finding a minimum spanning tree of a weighted graph G with n vertices and m edges has the time
complexity of: (1991)
(a) O(n2)
(b) O(m n)
(c) O(m + n)
(d) O(m log n)
(e) O(m2)
Ans: (b, d and e)
Sol: When Union- Find algorithm is used to detect cycle while constructing the MST time complexity is O(m log n) where m is the number of edges, and n is the number of vertices. Since m = 0 (n2) in a graph, options B and E are also correct as big-O specifies asymptotic upper bound only.
|
81 videos|113 docs|33 tests
|
FAQs on Previous Year Questions: Minimum Spanning Tree - Algorithms - Computer Science Engineering (CSE)
| 1. What is a minimum spanning tree? |  |
| 2. How is a minimum spanning tree different from a maximum spanning tree? |  |
| 3. What are some common algorithms used to find a minimum spanning tree? |  |
| 4. How does Kruskal's algorithm find a minimum spanning tree? |  |
| 5. When is it appropriate to use Prim's algorithm to find a minimum spanning tree? |  |
















