Previous Year Questions :Stack | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Q1: Let S1 and S2 be two stacks. S1 has capacity of 4 elements. S2 has capacity of 2 elements. S1 already has 4 elements: 100, 200, 300, and 400, whereas S2 is empty, as shown below. (2024 SET 2)
Stack S1
Stack S2
(a) 100, 200, 400, 300
(b) 200, 300, 400, 100
(c) 400, 200, 100, 300
(d) 300, 200, 400, 100
Ans: (b, c, d)
Sol: It is given that the size of S1 stack is 4 , size of S2 stack is 2 . we can push and pop at any time but for printing the element is only from the stack S1 . Here first Pop two items 400 , 300 form S1 and push it into S2
S1 = 200 , 100 ; S2 = 300 , 400 from top to bottom. Print 200 as output.
Pop 300 from S2 and push it into S1 , Print 300 . Now S1 = 100 , S2 = 400
Pop 400 form S2 and push it back into S1 . Print 400,100.
In this way, we can generate 200 , 300 , 400 , 100 as output.
First print 400 which top most element in S1 .
Pop 300 from S1 and push it into S2 .
Now print 200 , 100 from S1
Pop 300 from S2 and push it into S1 . print 300
In this way, we can generate
Pop 400 from S1 and push into S2 . Print 300 , 200
Pop 400 from S2 and push it into S1 .
So S1 = 400 , 100 . Now print 400 , 100
In this way, we can generate 300 , 200 , 400 , 100
can not be generated to print 100 we have to first pop 400 , 300 , 200 which is not possible because the size of S2 is two
Q2: Consider the operator precedence and associativity rules for the integer arithmetic operators given in the table below. (2024 SET1)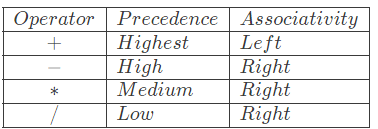
The value of the expression 3+1+5∗2/7+2−4−7−6/2 as per the above rules is _____
(a) 2
(b) 4
(c) 6
(d) 8
Ans: (c)
Sol:
Q3: Consider the following sequence of operations on an empty stack. (2021 SET 1)
push(54); push(52); pop(); push(55); push(62); s=pop();
Consider the following sequence of operations on an empty queue.
enqueue(21); enqueue(24); dequeue(); enqueue(28); enqueue(32); q=dequeue();
The value of s + q is ___________.
(a) 94
(b) 83
(c) 79
(d) 86
Ans: (d)
Sol: Stack:
- Push 54, push 52, pop (remove top element of stack)
- Now stack 54, (remove 52), push 55,push 62,pop
- Now top element is 62 (remove 62 as S)
S =62
Queue
- Enqueue 21Enqueue 24 dequeue (remove first element of queue)
- Now queue 24 (remove 21)Enqueue 28 Enqueue 32 dequeue
- Starting element is 24 ( remove 24 as Q)
- Q=24
S+Q=62+24 =68
Q4: The following postfix expression with single digit operands is evaluated using a stack: (2016)
8 2 3 ^/ 2 3∗+5 1∗− Note that ^ is the exponentiation operator. The top two elements of the stack after the first * is evaluated are
(a) 6,1
(b) 5,7
(c) 3,2
(d) 1,5
Ans: (a)
Sol: 8: Push. Stack becomes :8
2: Push. Stack becomes: 82
3: Push. Stack becomes: 823
^ : Pop and 3 and2 perform the operation2^3 and push the result to stack. Stack becomes : 88
/: Pop 8 and 8and perform the operation 8/8 and push the result to stack. Stack becomes :1
2: Push. Stack becomes :1 2
3: Push Stack becomes :1 2 3
*:Pop 3 and 2and perform the operation 2*3 and push the result to stack. Stack becomes :1 6
Q5:The result evaluating the postfix expression 10 5 + 60 6 / * 8 - is (2015 SET 3)
(a) 284
(b) 213
(c) 142
(d) 71
Ans: (c)
Sol: We have to keep symbol into stack and when we get two operands followed by operator. We will apply operator on last two operands.

Q6: Suppose a stack implementation supports an instruction REVERSE, which reverses the order of elements on the stack, in addition to the PUSH and POP instructions. Which one of the following statements is TRUE with respect to this modified stack?
(a) A queue cannot be implemented using this stack.
(b) A queue can be implemented where ENQUEUE takes a single instruction and DEQUEUE takes a sequence of two instructions.
(c) A queue can be implemented where ENQUEUE takes a sequence of three instructions and DEQUEUE takes a single instruction
(d) A queue can be implemented where both ENQUEUE and DEQUEUE take a single instruction each.
Ans: (c)
Sol: While ENQUEUE we RESVERSE the stack, PUSH the element and then again RESVERSE the stack. For DEQUE we simply POP the
element.
Option B can be used to get the first element from the stack by doing a POP after RESVERSE for DEQUEUE and PUSH for ENQUEUE . But we have to restore the stack using RESVERSE (otherwise next POP won't work) which means DEQUEUE actually needs 3 instructions and not 2.
Q7: The expression 1∗2∧3∗4∧5∗6 will be evaluated as (2009)
(a) 3230
(b) 1630
(c) 49152
(d) 173458
Ans: (c)
Sol: power has a higher priority than the multiplication
1*2^3*4^5*6
= 1 * (2^3) * (4^5 ) * 6
=1 * 8 * 1024 * 6
=49152
Q8: The infix expression A+(B−C)*D is correctly represented in prefix notation as (2006)
(a) A+B-C*D
(b) +A*-B C D
(c) A B C -D*+
(d) A+B C-D*
Ans: (c)
Sol: Scan Right to Left
Stack : * ) -
Pop - ) by seeing (
Stack: *
Pop * as incoming is +
Stack : +
Output : +A*-BCD
Q9: Assume that the operators +,−,× are left associative and ^ is right associative. The order of precedence (from highest to lowest) is ^ ,×,+,−. The postfix expression corresponding to the infix expression a+ b × c−d ^e^ f is (2009)
(a) a b c x+ def^^-
(b) a b c x+ de^ f^
(c) a b+ cx -e^ f^
(d) -+ax bc ^^ de f
Ans: (a)
Sol: Here is the procedure first :
Scan Infix Expression from left to right whenever you see operand just print it.
But, in case of operator
if(stack is empty) then push it.
if(precedence(to s) > precedence(current operator) ) push it. where, t o s means top of stack.
else if (precedence(t o s) > precedence(current operator) ) pop and print.
else if (precedence(t o s) == precedence(current operator) ) then check for associativity. In case Operators are Left to right then pop and print it otherwise push the current operator (Right to Left Associativity)
And once you have scanned infix expression completely. Make sure pop all the element and print it in same order.
Q10: Stack A has the entries a, b, c (with a on top). Stack B is empty. An entry popped out of stack A can be printed immediately or pushed to stack B. An entry popped out of the stack B can be only be printed. In this arrangement, which of the following permutations of a, b, c are not possible? (2008)
(a) b a c
(b) b c a
(c) c a b
(d) a b c
Ans: (c)
Q11: Consider the following C program: (2007)

What is the output of the program for the following input?
5 2 *3 3 2 + * +
(a) 15
(b) 25
(c) 30
(d) 150
Ans: (b)
Sol: 25let first part
5 ----push
2------push
push------ 5*2 =10. (pops 5 and 2)
Q12: The following postfix expression with single digit operands is evaluated using a stack: (2007)
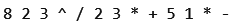
Note that ^ is the exponentiation operator. The top two elements of the stack after the first * is evaluated are:
(a) 6,1
(b) 5, 7
(c) 3, 2
(d) 1, 5
Ans: (a)
Sol: 8 : PUSH . Stack becomes :8
2 : PUSH .Stack becomes :82
3 : PUSH . Stack becomes :823
^ : POP 3 and 2 and perform the operation 2 ^ 3 and push the result to stack. Stack becomes:88
∕ : POP 8 and 8 and perform the operation 8 ∕ 8 and push the result to stack. Stack becomes:1
2 : PUSH . Stack becomes:12
3 : PUSH . Stack becomes:123
∗ : POP 3 and 2 and perform the operation 2 ∗ 3 and push the result to stack.
Q13: A function f defined on stacks of integers satisfies the following properties. f(∅)=0and f(push(S , i ))=max (f (S),0)+ i for all stacks S and integers 2, , -3, 2, -1, 2 in order from bottom to top, what is f(S)? (2005)
(a) 6
(b) 4
(c) 3
(d) 2
Ans: (c)
Sol: i : Element to be pushed
Initial State f(∅)For Empty Stack f(S) is 0
Then we push each element (i)one by one and calculate f(s)
for each insertion as given
is the function to compute f(S) for each insertions
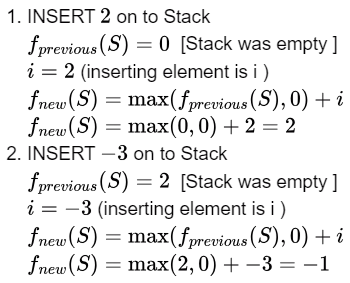
Similarly,
i: The element to be pushed
S: Stack
Initially f(S)=0.
Q14: A program attempts to generate as many permutations as possible of the string, 'a b c d' by pushing the characters a, b, c, d in the same order onto a stack, but it may pop off the top character at any time. Which one of the following strings CANNOT be generated using this program? (2004)
(a) ab c d
(b) dc b a
(c) c bad
(d) c ab d
Ans: (d)
Sol: this sequence is not possible because 'a' can not be popped before 'b' any how
Q15: Assume that the operators +, -, x , are left associative and ^ is right associative. the order of precedence (from highest to lowest) is ^, x , +, -. The postfix expression corresponding to the infix expression a + b x c -d ^e ^ f is (2004)
(a) a b c x+ def^^-
(b) a b c x+ de^ f^
(c) a b+ cx -e^ f^
(d) -+ax bc ^^ de f
Ans: (a)
Sol: Here is the procedure first : Scan Infix Expression from left to right whenever you see operand just print it. But, in case of operator if(stack is empty) then push it. if(precedence( to) < precedence(current operator) ) push it. where , to means top of stack. else if (precedence(to) > precedence(current operator) ) pop and print. else if (precedence(to) == precedence(current operator) ) then check for associativity. In case Operators are Left to right then pop and print it otherwise push the current operator (Right to Left Associativity) And once you have scanned infix expression completely. Make sure pop all the element and print it in same order.
Here, the infix expression is a + b × c − d ^ e ^ f
a : print it
+ : push into the Operator Stack
b : print it
∗ : its having higher precedence than + then push into Operator Stack
c : print it
′ − ′ : ′ − ′ is having less precedence than ′ ∗ ′ so pop from operator stack and print
′ ∗ ′ .after this stack will be having ′ + ′ on top. which is having same precedence as
′ − ′ but both are left to right associative then just pop + and print it. Now stack is
empty. Push ′ − ′ to it.
d : print it
' ^ ' : top of the stack is having ′ − ′ .' ^ ' has higher precedence than ′ − ′ .so simply
push ' ^ ' into stack
e : print it.
' ^ ' : Now top of the stack is ' ^ ' and has same precedence so associativity will come
to picture. Since ' ^ ' is right associative as given in question. So ' ^ ' will be pushed.
f : print it.
Now, we have scanned entire infix expression. Now pop the stack until it becomes empty. This way you will get a b c × + d e f ^ ^ − .
Q16: The best data structure to check whether an arithmetic expression has balanced parenthesis is a: (2017)
(a) Queue
(b) Stack
(c) Tree
(d) List
Ans: (b)
Sol: STACK scan the expression from left to right whenever a left p a r a n thesis is encountered just PUSH it into stack and whenever a right p a r a n thesis is encountered just POP it from stack. If at the end of expression we are left with an empty stack then it is a correctly parenthesized expression.
Q17: A single array A[1...MAXSIZE] is used to implement two stacks. The two stacks grow from opposite ends of the array. Variables top1 and top 2 (top1 < top 2) point to the location of the topmost element in each of the stacks. If the space is to be used efficiently, the condition for "stack full" is (2004)
(a) (top1 = MAXSIZE/2) and (top2 = MAXSIZE/2+1)
(b) (top1 + top2 = MAXSIZE
(c) (top1 = MAXSIZE/2) or (top2 = MAXSIZE)
(d) top1 = top2 -1
Ans: (d)
Sol: Since the stacks are growing from opposite ends, initially top1 =1 and top2 =MAXSIZE. Now, to make the space usage most efficient we should allow one stack to use the maximum possible space as long as other stack doesn't need it. So, either of the stack can grow as long as there is space on the array and hence the condition must be top1 =1 and top2 -1.
Q18: Let S be a stack of size n ≥1. Starting with the empty stack, suppose we push the first n natural numbers in sequence, and then perform n pop operations. Assume that Push and Pop operation take X seconds each , and Y seconds elapse between the end of the one such stack operation and the start of the next operation. For m ≥ 1, define the stack-life of m as the time elapsed from the end or Push (m) to the start of the pop operation that removes m from S . The average stack-life of an element of this stack is (2003)
(a) n(X+Y)
(b) 3Y+2X
(c) n(X+Y)-X
(d) Y+2X
Ans: (b)
Sol: Let us represent stack-life of I th element as S(I). The Ith element will be in stack till (n- i) elements are pushed and popped. Plus one more Y for the time interval between the push of I th element and the 1th element. So,
S (i) = Y+2.(n I) (Y+X) 2.(n I) Z=Y +2nZ -2 IZ
where Z=Y+X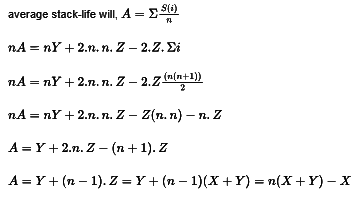
Q19: To evaluate an expression without any embedded function calls (2002)
(a) O ne stack is enough
(b) Two stack are needed
(c) As many stacks as the height of the expression tree are needed
(d) Turning machine is needed in the general case
Ans: (a)
Sol: Expression without any calls in it ⇒1+2*3- 4
Expression with embedded calls ⇒1+fun 1(a, b, c)* fun 2(3.4, 58 ) -fun3(x, y z;
First we can convert Infix to Postfix using single stack (Using it as operator stack)
Then we can evaluate that expression using Single stack.
Q20: Which of the following is essential for converting an infix expression to the postfix form efficiently? (1997)
(a) An operator stack
(b) An operand stack
(c) An operand stack and an operator stack
(d) A parse tree
Ans: (a)
Sol: First of all, this question must be clear in our mind and i.e. Why do we need to convert infix expression postfix expression?
"Conventional notation is called infix notation. The arithmetic operators appears between two operands. Parentheses are required to specify the order of the operations. For example: a + (b * c).
Post fix notation (also, known as reverse Polish notation) eliminates the need for parentheses.
There are no precedence rules to learn, and parenthesis are never needed. Because of this simplicity, some popular hand-held calculators use postfix notation to avoid the complications of multiple sets of parentheses.
The operator is placed directly after the two operands it needs to apply. For example: a b c * +
You got the answer of Why?
Now, it's time to know what?
What is Operand Stack?
When we evaluate a given postfix expression, then we only push the operands into the stack but not any operator. So, the stack used in postfix evaluation called operand stack.
What is Operator Stack?
When we convert an infix notation into postfix notation, then we only push the operators into the stack but not any operand. So, stack used in the conversion from infix to postfix is called operator stack.
Algorithm to convert Infix into Postfix expression using operator stack:
Input is-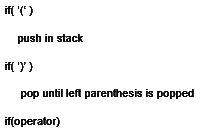 1. Lower priority is in input then pop
1. Lower priority is in input then pop
2. Higher priority is in input then push
3. Same r priority is pop except exponent Operator
if(Operand)
Ignore
Q21: The postfix expression for the infix expression A+B*(C+D)/F+D*E is: (1995)
(a) AB + CD + *F/D +E*
(b) ABCD + *F/DE* ++
(c) A * B + CD/F *DE ++
(d) A + *BCD/F* DE ++
Ans: (b)
Sol: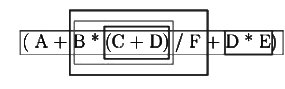
Thus before considering + which has the least priority, we get A+(BCD+*F/)+(DE*)
Now if we assume left associativity for+
So, considering right associativity for +
Q22: Which of the following permutations can be obtained in the output (in the same order) using a stack assuming that the input is the sequence 1, 2, 3, 4, 5 in that order? (1994)
(a) 3, 4, 5, 1, 2
(b) 3, 4, 5, 2, 1
(c) 1, 5, 2, 3, 4
(d) 5, 4, 3, 1, 2
Ans: (b)
Sol: Push 1 push 2push 3pop 3 push 4 pop 4 push 5 pop 5 pop 2 pop 1 then o/p is 3,4,5,2,1
Q23: Choose the correct alternatives (more than one may be correct) and write the corresponding letters only:
The following sequence of operations is performed on a stack: PUSH (10), PUSH (20), POP, PUSH (10), PUSH (20),
POP, POP, POP, PUSH (20), POP The sequence of values popped out is (1991)
(a) 20,10,20,10,20
(b) 20,20,10,10,20
(c)10,20,20,10,20
(d) 20,20,10,20,10
Ans: (b)
Sol: Let us try something different when you read the word pop then delete the last pushed element and print it. Now, delete the push word which we have already executed. Now, go on from left to right and do the same.
So, output will be 20,20,10,10,20.
|
159 docs|30 tests
|
FAQs on Previous Year Questions :Stack - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is a stack in computer science? |  |
| 2. How is a stack different from a queue? |  |
| 3. What are some common operations performed on a stack? |  |
| 4. How is a stack implemented in computer memory? |  |
| 5. What are some real-world applications of a stack data structure? |  |
















