Previous Year Question: Queue | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Q1: Consider a sequence a of elements a0 =1,a1=5,a2 =7,a3=8,a4 =9,and a5 =2.The following operations are performed on a stack S and a queue Q, both of which are initially empty. (2023)
I: push the elements of a from a0toa5 in that order into S.
II: enqueue the elements of a from a0toa5 in that order into Q.
III: pop an element from S.
IV: dequeue an element from Q.
V: pop an element from S.
VI: dequeue an element from Q.
VII: dequeue an element from Q and push the same element into S.
VIII: Repeat operation VII three times.
IX: pop an element from S.
X: pop an element from S .
The top element of S after executing the above operations is ___.
(a) 7
(b) 8
(c) 9
(d) 2
Ans: (b)
Sol: Given initial elements: =1,a1=5,a2 =7,a3=8,a4 =9,and a5 =2.
1) Push all the elements into the stack S in the same order:

2) Push all the elements into the queue Qin the same order:
3) Pop(S):
4) Dequeue(Q):
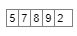 7) Dequeue (Q) and push the same element into S
7) Dequeue (Q) and push the same element into S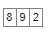

8) repeat step 7 three times we get:
First time: second time:
second time:


third time:  9 ) pop (S):
9 ) pop (S):  10 ) pop(S):
10 ) pop(S): 
from the resultant stack S topmost element is 8
Q2: Consider the queues Q1 containing four elements and Q2 containing none (shown as the Initial State in the figure). The only operations allowed on these two queues are Enqueue (Q ,element) and D e q u e u e ( Q ) Dequeue(Q). The minimum number of E n q u e u e Enqueue operations on Q1 required to place the elements of Q1 in Q2 in reverse order (shown as the Final State in the figure) without using any additional storage is (2022)
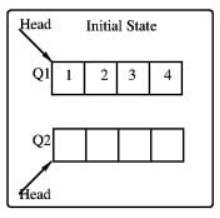
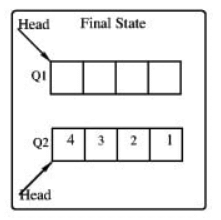 (a) 4
(a) 4
(b) 2
(c) 0
(d) 1
Ans: (c)
Sol: By convention, the end of the sequence at which elements are added is called the back, tail, or rear of the queue, and the end at which elements are removed is called the head or front of the queue.
Head means Dequeue.
We want the following situation.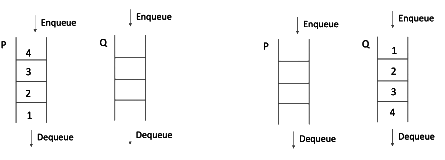
Before that, One quick question- Can you reverse a queue in place by just using simple enqueue and dequeue as asked in question?.
If queue is just having 2 elements then yes otherwise no.
Let me first divide 4 elements into 2-2 elements each.
Step 1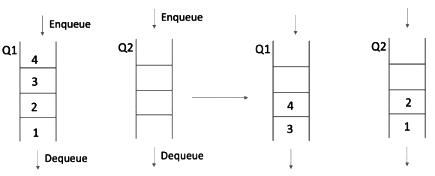
Till now, NO enqueue to Q1.
Now reverse . This doesn’t cost any ENQUEUE to Q1
Step2: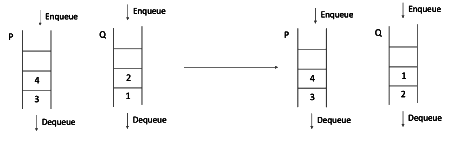
Step 3: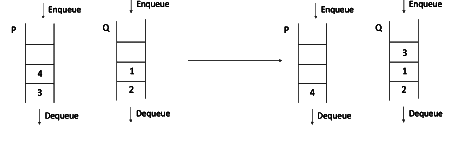 Step 4:
Step 4:
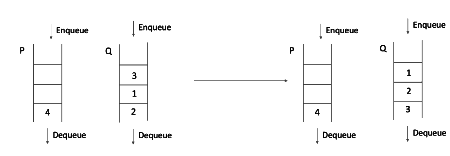 Step 5:
Step 5:
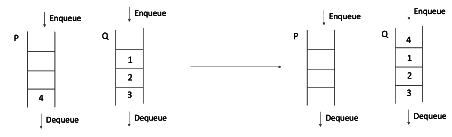
Step 6: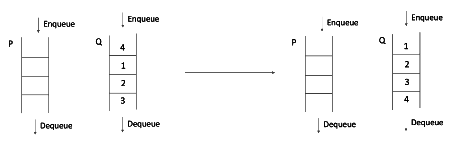
Q3: A queue is implemented using a non-circular singly linked list. The queue has a head pointer and a tail pointer, as shown in the figure. Let n denote the number of nodes in the queue. Let enqueue be implemented by inserting a new node at the head, and dequeue be implemented by deletion of a node from the tail. (2018)

Which one of the following is the time complexity of the most time-efficient implementation of enqueue and dequeue, respectively, for this data structure?
(a) Θ(1),Θ(1)
(b) Θ(1),Θ(n)
(c) Θ(n) , Θ(1)
(d) Θ(n) ,Θ(n)
Ans: (b)
Sol: New node to be inserted is P
Time Complexity =0(1) Because only pointer manipulation is involved which takes constant time.
Delete Tail
 Time Complexity = Time for Traversing list, free the last node and keep track of Tail pointer =0(n)
Time Complexity = Time for Traversing list, free the last node and keep track of Tail pointer =0(n)
Q4: Which of the following data structure is useful in traversing a given graph by breadth first search? (2017)
(a) Stack
(b) Queue
(c) List
(d) None of the above
Ans: (b)
Q5: A circular queue has been implemented using a single linked list where each node consists of a value and a single pointer pointing to the next node. We maintain exactly two external pointers FRONT and REAR pointing to the front node and the rear node of the queue, respectively. Which of the following statements is/are CORRECT for such a circular queue, so that insertion and deletion operation can be performed in O (1) time ? (2017 SET 2)
I. Next pointer of front node points to the rear node.
II. Next pointer of rear node points to the front node.
(a) I only
(b) II only
(c) Both I and II
(d) Neither I nor II
Ans: (b)
Sol:
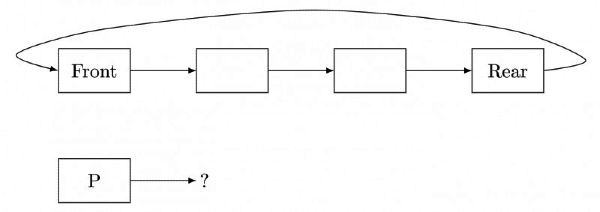
This is how the things look. We do insertion by cutting in between Rear and Front and we do deletion by forwarding the Front pointer and updating the Rear accordingly.
Q6: Let Q denote a queue containing sixteen numbers and S be an empty stack. Head(Q) returns the element at the head of the queue Q without removing it from Q. Similarly Top(S) returns the element at the top of S without removing it from S. Consider the algorithm given below. (2016 SET 1)
The maximum possible number of iterations of the while loop in the algorithm is_________.
(a) 16
(b) 64
(c) 256
(d) 1027
Ans: (c)
Sol: Now, 16 will be first pushed into the stack, So, now stack top is 16 and HEAD(Q) is 15 , So 16 will be popped out of the stack ( since, "if S is Empty OR
TOP(S) ≤/head(Q "returns false, hence else part will be executed) and enqueued into the Queue. ,
So, after two iterations Queue elements will be → 15,14,13,..., 2,1,16 and stack will be empty.}
Similarly, each of the elements 15,14,13,..., 2,
will be pushed into the stack and immediately popped out of the stack(when popped out of the stack then also enqueue into the queue).So after 30 iterations stack will be empty and Queue contains will be like ⇒1,16,15,14 ,..., 2,.
Now 1 will be Dequeued and pushed into the stack. Once 1 is pushed into the stack, it will never be popped(or we can say never be enqueued into the Queue again) because in order to Pop 1, there should be an element into the Queue which is less than 1 and that element comes at the front of the queue, since there is no element currently present in the Queue which is less than 1, there is no way to pop 1.
So, after 31 iterations Queue is ⇒16,15,14 ,..., 2,. and stack contains 1.
Now, the problem boils down to Queue with 15elements.
Using the similar logic we can say after another 29iterations (Total =31+29)Queue will be like ⇒16,15,14 ,..., 3 and stack contains 1,2(stack top is 2) and then 2 will remain there in the stack forever.
Q7: A queue is implemented using an array such that ENQUEUE and DEQUEUE operations are performed efficiently. Which one of the following statements is CORRECT (n refers to the number of items in the queue)? (2016 SET1 )
(a) Both operations can be performed in O(1) time
(b) At most one operation can be performed in O(1) time but the worst case time for the other operation will be Ω(n)
(c) The worst case time complexity for both operations will be Ω(n)
(d) Worst case time complexity for both operations will be Ω(log n)
Ans: (a)
Sol: Consider a normal array implementation of a queue. We’ll have 2pointers Front and Rear where Front points to the first element of the queue and Rear points to the next free space. When queue is full Rear points to NULL
The below figure depicts the Queue full condition and then a DEQUEUE is performed which removes element 4In the second part of the figure, all elements are shifted by one position or else we won’t be able to make use of the free space for the next element to be inserted. So, this means Θ(n)operations for DEQUEUE where as ENQUEUE can be done in 0(1)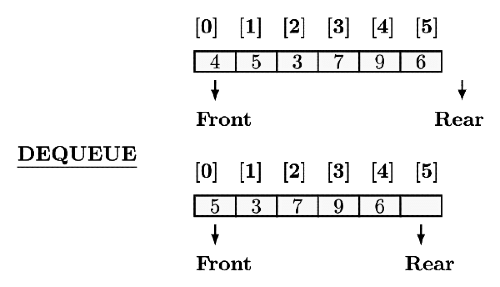
But we can in fact do both ENQUEUE and DEQUEUE operations in 0(1) and fully utilize the array space by smartly using the and pointers as shown in DEQUEUE opt. If MAX denote the total size of the array, here,
Q8: Consider the following operation along with Enqueue and Dequeue operations on queues, where k is a global parameter. (2013)

What is the worst case time complexity of a sequence of n queue operations on an initially empty queue?
(a) Θ(n)
(b) Θ(n+ k)
(c) Θ(n k)
(d) Θ(n 2)
Ans: (a)
Sol: There are three possible operations on queue- Enqueue, Dequeue and Multi Dequeue. Multi Dequeue is calling Dequeue multiple times based on a global variable k. Since, the queue is initially empty, whatever be the order of these operations, there cannot be more number of Dequeue operations than Enqueue operations. Hence, the total number operations will be n only.
Q9: Suppose a circular queue of capacity (n-1) elements is implemented with an array of n elements. Assume that the insertion and deletion operations are carried out using REAR and FRONT as array index variables, respectively. Initially, REAR = FRONT = 0. The conditions to detect queue full and queue empty are (2012)
(a) full: (REAR+1) mod n == FRONT
empty: REAR == FRONT
(b) full: (REAR+1) mod n == FRONT
empty: (FRONT+1) mod n == REAR
(c) full: REAR == FRONT
empty: (REAR+1) mod n == FRONT
(d) full: (FRONT+1) mod n == REAR
empty: REAR == FRONT
Ans: (a)
Sol: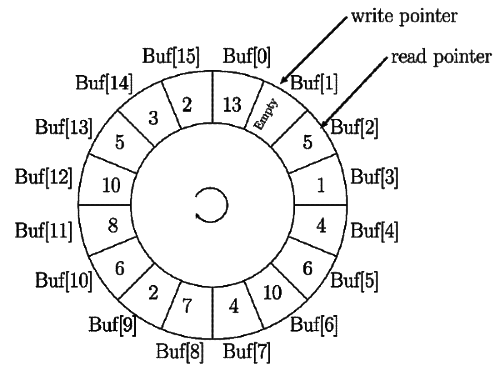 REAR= WRITE
REAR= WRITE
FRONT= READ
full: (REAR +1) mod n ==FRONT
empty: REAR==FRONT
Q10: Suppose you are given an implementation of a queue of integers. The operations that can be performed on the queue are: (2007)
i . is Empty(Q) returns true if the queue is empty, false otherwise.
ii. delete(Q) deletes the element at the front of the queue and returns its value.
iii. insert(Q ,i ) inserts the integer i at the rear of the queue.
Consider the following function
What operation is performed by the above function f ?
(a) Leaves the queue Q unchanged
(b) Reverses the order of the elements in the queue Q
(c) Deletes the element at the front of the queue Q and inserts it at the rear keeping the other elements in the same order
(d) Empties the queue Q
Ans: (b)
Sol:
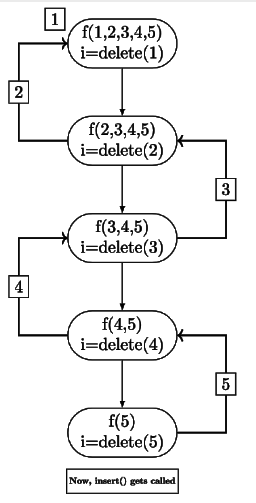
insert( ) will inserts the values in reverse order.
Q11: An implementation of a queue Q, using two stacks S1 and S2, is given below: (2006)
Let n insert and m(≤n) delete operations be performed in an arbitrary on an empty queue Q, Let x and y be the number of push and pop operations performed respectively in the processes. Which one of the following is true for all m and n ?(a) m +n ≤ x ≤ 2n and 2m ≤ y ≤ n +m
(b) m +n ≤ x ≤ 2n and 2m ≤y≤ 2n
(c) 2m+n ≤ x ≤ 2n and 2m≤ y ≤ n+ m
(d) 2m+n ≤ x ≤ 2n and 2m ≤ y ≤ 2n
Ans: (a)
Sol: The order in which insert and delete operations are performed matters here.
The best case: Insert and delete operations are performed alternatively. In every delete operation, 2pop and 1 push operations are performed. So, total m+ n push (n push for insert() and m push for delete()) operations and 2 m pop operations are performed.
The worst case: First n elements are inserted and then m elements are deleted. In first delete operation, n+1 pop operations and n push operation are performed. Other than first, in all delete operations, 1 pop operation is performed. So, total m +n pop operations and 2npush operations are performed (n push for insert() and m push for delete()
Q12: A priority queue Q is used to implement a stack that stores characters. PUSH (C) is implemented as INSERT (Q,C,K) where K is an appropriate integer key chosen by the implementation. POP is implemented as DELETEMIN (Q). For a sequence of operations, the keys chosen are in (1997)
(a) non-increasing order
(b) non-decreasing order
(c) strictly increasing order
(d) strictly decreasing order
Ans: (d)
Sol: Implementing stack using priority queue require first element inserted in stack will be deleted at last, and to implement it using delete min() operation of queue will require first element inserted in queue must have highest priority.
So the keys must be in strictly decreasing order.
Q13: Consider the following statements: (1996)
(i). First-in-first out types of computations are efficiently supported by STACKS.
(ii). Implementing LISTS on linked lists is more efficient than implementing LISTS on an array for almost all the basic LIST operations.
(iii). Implementing QUEUES on a circular array is more efficient than implementing QUEUES on a linear array with two indices.
(iv). Last-in-first-out type of computations are efficiently supported by QUEUES.
(a) (ii) and (iii) are true
(b) ( i) and (ii) are true
(c) ( iii) and (iv) are true
(d) (ii) and (iv) are true
Ans:(a)
Q14: What is the minimum number of stacks of size n required to implement a queue to size n ? (2001)
(a) One
(b) two
(c) three
(d) four
Ans:(b)
Sol: A queue can be implemented using two stacks.
Let queue be represented as " q" and stacks used to implement q be "stack1" and "stack2".
q can be implemented in two ways:
Method 1 (By making E n Queue operation costly)
This method makes sure that newly entered element is always at the bottom of stack 1, so that de Queue operation just pops from stack1. To put the element at top of stack1, stack2 is used.|
e n Queue (q, x )
1.While stack1 is not empty, push everything from stack1 to stack2.
2.Push x to stack1 (assuming size of stacks is unlimited).
3.Push everything back to stack1.
e n Queue (q)
1. If stack1 is empty then error
2.Pop an item from stack1 and return it
Method 2 (By making de Queue operation costly)
In this method, in e n-queue operation, the new element is entered at the top of stack1. In de-queue operation, if stack2 is empty then all the elements are moved to stack2 and finally top of stack2 is returned.
e n Queue (q, x )
1. Push x to stack1 (assuming size of stacks is unlimited).
e n Queue (q)
1. If both stacks are empty then error.
2.If stack2 is empty While stack1 is not empty, push everything from stack1 to stack2.
3. Pop the element from stack2 and return it.
|
159 docs|30 tests
|
FAQs on Previous Year Question: Queue - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is a Queue in Computer Science Engineering (CSE)? |  |
| 2. How is a Queue different from a Stack in Computer Science Engineering (CSE)? |  |
| 3. What are the operations that can be performed on a Queue in Computer Science Engineering (CSE)? |  |
| 4. How is a Queue implemented in Computer Science Engineering (CSE)? |  |
| 5. What are the real-world applications of Queues in Computer Science Engineering (CSE)? |  |
















