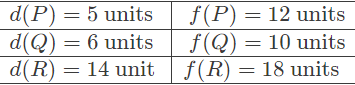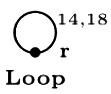Q1: Let U = {1, 2, 3}. Let 2U denote the powerset of U. Consider an undirected graph G whose vertex set is 2U. For any A, B ∈ 2U, (A, B) is an edge in G if and only if (i) A ≠ B, and (ii) either A ⊆ B or B ⊆ A. For any vertex A in G, the set of all possible orderings in which the vertices of G can be visited in a Breadth First Search (BFS) starting from A is denoted by B(A).
If ∅ denotes the empty set, then the cardinality of B(∅) is_____. (2023)
(a) 524
(b) 63218
(c) 5040
(d) 2540
Ans: (c)
Sol: Given that U = {1,2,3}→ |U| = 3 → Vertex set = {∅, {1},{2},{3},{1,2},{1,3},{2,3}, {1,2,3}} and cardinality is 8.
There is an edge between A and B vertices if either of vertex set is proper subset to other vertex.
As we know ∅ is proper subset to every other set in the vertex set except itself.
That implies, ∅ is connected with 7 vertices directly, these 7 vertices can be visited in any order in BFS.
Therefore No. of BFS orders = 7! = 120 x 6 x 7 = 5040.
Q2: An articulation point in a connected graph is a vertex such that removing the vertex and its incident edges disconnects the graph into two or more connected components.
Let T be a DFS tree obtained by doing DFS in a connected undirected graph G.
Which of the following options is/are correct? (2021 SET-1)
(a) Root of T can never be an articulation point in G.
(b) Root of T is an articulation point in G if and only if it has 2 or more children.
(c) A leaf of T can be an articulation point in G.
(d) If u is an articulation point in G such that x is an ancestor of u in T and y is a descendent of u in T, then all paths from x to y in G must pass through u.
Ans: (b)
Sol:
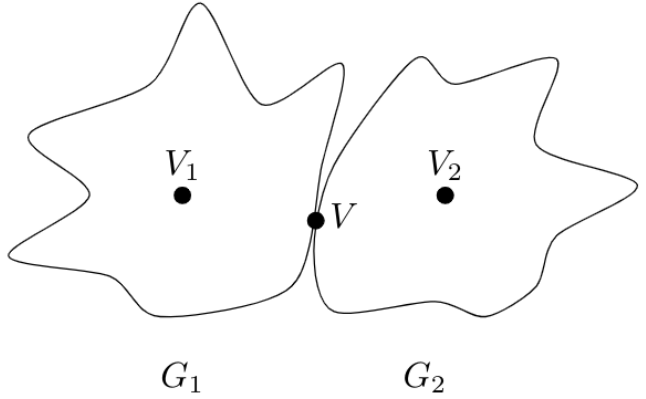
As per the option B it says root of T can be an articulation point in G if and only if it has 2 or more children, now here for simplicity I have taken simple case where root will have 2 children and I will tell you for the generalized case later. Also as its double implication lets see it as separately
Case 1: If root is articulation point then root will have 2 or more children If a vertex is articulation point then its removal disconnects the graph into 2 or more components means there must exist at least 2 vertices for which each and every path in between them will pass through articulation point and removal of articulation point will destroy all the paths in between them and thereby disconnecting the graph into components, otherwise that vertex can not be an articulation point because even if we remove that vertex still every pair of vertices has some other path and hence graph wont get disconnected.
Now when we start DFS Traversal from vertex V (articulation point) we may visit either the vertex from G1 or G2 first, lets say we visited vertex of G2 first now during the DFS traversal which becomes child of V now we can never visit any vertex in G1 unless and until we do not use vertex V because every path will go through vertex V only, and by the nature of DFS no vertex during the traversal of sub-graph G2 can visit the vertex V again as it will be having Gray color/ not yet finished (refer DFS algorithm from CLRS for better understanding) and because of this property all the vertices in G2 will be exhausted and we will be back to the vertex V but vertex V still has path to the unvisited vertices of sub-graph G1 and hence the first vertex which will be visited in G1 will become the new child of V thereby making 2 children for the root vertex V which is the articulation point.
Case 2: If root vertex has 2 or more children then it is articulation point
Lets say in an undirected graph if root has 2 children then it is true that there is no path between the vertices in left sub-tree and right sub-tree of vertex V (w.r.t DFS traversal tree) because if there had been any path between the left and right sub-tree the in that case if we start with right child then before reaching to the root all the vertices in left sub-tree would have been visited and root had only single child but it is contradiction as root has 2 children and hence there can be no path between the left and right sub-tree of vertex V, thereby making it the only vertex through which vertices in left and right sub-tree are connected
Hence above two cases proves the option B is correct and A is incorrect
For the generalized case visualize star graph with many vertices where center is articulation point, now you got the intuition and apply this on any graph!
Lets understand option C.
Option C says that leaf of tree T can be an articulation point, its FALSE because if some vertex is leaf of tree T then all the vertices to which it connects are already been visited which indicates that even without using this leaf vertex there exists path between all of its neighbors and hence it can not be an articulation point.
Hence option C is incorrect
Now option D
Option D talks about ancestors and decedents X and Y and says that if X is ancestor of U in T and Y is decedent then all the paths between X and Y must pass through U but we have counter for this as shown below.
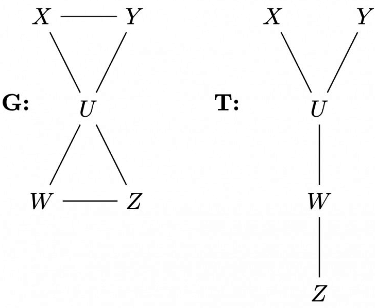
Hence option D is incorrect
Q3: G is an undirected graph with vertex set {v1, v2, v3, v4, v5, v6, v7} and edge set {v1v2, v1v3, v1v4, v2v4, v2v5, v3v4, v4v5, v4v6, v5v6, v6v7 }. A breadth first search of the graph is performed with v1 as the root node. Which of the following is a tree edge? (2020)
(a) v2v4
(b) v1v4
(c) v4v5
(d) v3v4
Ans: (b)
Sol: V1 is adjacent to V2, V3,V4
so queue state will be

After V1 is popped the queue will contain V2 V3 V4 and V5
Note: the above elements can appear in any order after V1
so, V4 can be popped first and you may think that the answer is V4V5. But here V2 V3 and V5 can also be popped first. so V4V5 may be an edge which will not be included in the BFS tree(as V2 also has an edge to V5).
But V1V4 edge will always be included in the BFS tree as we have taken V1 as the root.
So, answer is b)V1V4
Q4: Which of the following is application of Breath First Search on the graph? (2018)
(a) Finding diameter of the graph
(b) Finding bipartite graph
(c)Both (A) and (B)
(d) None of the above
Ans: (c)
Sol:
Some of the important applications of BFS are:
1. Finding diameter of the graph.
2. Finding the bipartite graph.
3. Peer to peer networks.
4. Shortest Path and Minimum Spanning Tree for the unweighted graph.
5. Social Networking Websites.
6. Crawlers in Search Engines.
7. GPS Navigation Systems.
8. Broadcasting in Network.
9. In Garbage Collection.
10. Cycle detection in the undirected graph.
11. Ford Fulkerson algorithm.
12. Path finding.
13. Finding all nodes within a connected component.
Q5: Let G be a simple undirected graph. Let TD be a depth first search tree of G. Let TB be a breadth first search tree of G. Consider the following statements.
(1) No edge of G is a cross edge with respect to TD. (A cross edge in G is between two nodes neither of which is an ancestor of the other in TD.)
(II) For every edge (u, v) of G, if u is at depth i and v is at depth j in TB, then |i-j| = 1.
Which of the statements above must necessarily be true? (2018)
(a) I only
(b) II only
(c) Both I and II
(d) Neither I nor II
Ans: (a)
Sol: I. Undirected graph cant have cross edges in DFS forest. (Only directed graphs can have) (Hence I is True)
(If you do not agree just try it with taking examples. You cant draw)
II. Just draw a triangle SAB. Source is S. Vertex A and B are at same level hence distance 1. So here |i - j| = 0. (Hence II is false)
Hence answer is (A).
Anyway, II is simple to understand from the above explanation.
Those who did not get I, you may see Theorem 22.10 in Cormen)
Q6: The Breadth First Search (BFS) algorithm has been implemented using the queue data structure. Which one of the following is a possible order of visiting the nodes in the graph below? (2017 SET-2)
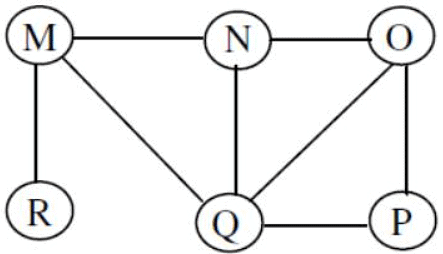
(a) MNOPQR
(b) NQMPOR
(c) QMNROP
(d) POQNMR
Ans: (d)
Sol: Here, we can see that only option (D) is following BFS sequence properly.
- As per BFS, if we start from M then RQN (immediate neighbors of M) have to come after it in any order but in A here, O comes in between. So, it is not BFS.
- As per BFS, if we start from N then QMO has to come after it in any order but in B here, P comes. So, it is not BFS.
- As per BFS, if we start from Q then MNOP has to come after it in any order but in C here, R comes. So, it is not BFS.
But D is following the sequences.
So, D is the correct answer.
Q7: Breadth First Search(BFS) is started on a binary tree beginning from the root vertex. There is a vertex t at a distance four from the root. If t is the n-th vertex in this BFS traversal, then the maximum possible value of n is (2016 SET-2)
A 16
(b)15
(c) 31
(d) 32
Ans: (c)
Sol: No of nodes at level 0(root) of tree ⇒ 1
No of nodes at level 1 of tree ⇒ 2
No of nodes at level 2 of tree ⇒ 4
No of nodes at level 3 of tree ⇒ 8
No of nodes at level 4 of tree ⇒ 16
Last node in level 4th is the node we are looking for ⇒ 1 + 2 + 4 + 8 + 16 ⇒ 31
Q8: Consider the following directed graph:
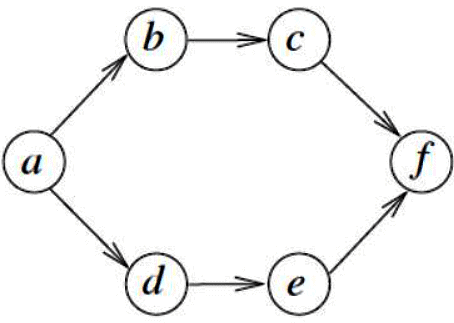
The number of different topological orderings of the vertices of the graph is (2016 SET-1)
(a) 4
(b) 5
(c) 6
(d) 7
Ans: (c)
Sol: Here, start with a and end with f.
a ______ f
Blank spaces are to be filled with b, c, d, e such that b comes before c, and d comes before e.
Number of ways to arrange b, c, d, e such that b comes before c and d comes before e, will be 4!/(2! x 2!) = 6
Q9: Let G = (V, E) be a simple undirected graph, and s be a particular vertex in it called the source. For x ∈ V, let d(x) denote the shortest distance in G from s to x. A breadth first search (BFS) is performed starting at s. Let T be the resultant BFS tree. If (u, v) is an edge of G that is not in T, then which one of the following cannot be the value of d(u)-d(v)? (2015 SET-1)
(a) -1
(b) o
(c) 1
(d) 2
Ans: (d)
Sol: d(u) - d(v) = 0 is possible when both u and v have an edge from from a common node t and t is in the shortest path from s to u and v.
d(u) - d(v) = 1 is possible when v and another node t are in the shortest path from s to u and both t and v are siblings- same distance from s to both t and v causing t - u edge to be in BFS tree and not v - u.
d(u)d(v) = -1 is possible as explained above by interchanging u and v.
d(u) d(v) = 2 is not possible. This is because on BFS traversal we either visit u first or v. Let's take u first. Now, we put all neighbors of u on
queue. Since v is a neighbor and v is not visited before as assumed, d(v) will become d(u) + 1. Similarly, for v being visited first.
Q10: Suppose depth first search is executed on the graph below starting at some unknown vertex. Assume that a recursive call to visit a vertex is made only after first checking that the vertex has not been visited earlier. Then the maximum possible recursion depth (including the initial call) is _________. (2014 SET-3)
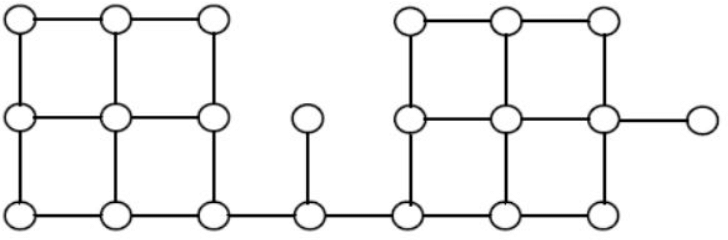
(a) 16
(b) 19
(c) 17
(d) 20
Ans: (b)
Sol: Total 21 nodes are there. 2 nodes require back track here in this question.
So, max recursion depth is 21 - 2 = 19
(Do DFS from extreme ends such that max recursion depth will occur. i.e., take leftmost top node as initial node for DFS as shown in below image)
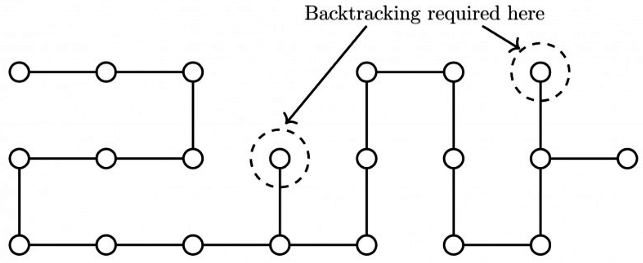
Note:- Backtrack means it reduces recursion depth in stack.
Q11: Let G be a graph with n vertices and m edges. What is the tightest upper bound on the running time of Depth First Search on G, when G is represented as an adjacency matrix? (2014 SET-1)
(a) Θ(n)
(b) Θ(n + m)
(c) Θ(n2)
(d) Θ(m2)
Ans: (c)
Sol: Takes O(m + n) time when the graph is represented using adjacency list. In adjacency matrix representation, graph is represented as an n∗ n matrix. To do DFS, for every vertex, we traverse the row corresponding to that vertex to find all adjacent vertices (In adjacency list representation we traverse only the adjacent vertices of the vertex). Therefore time complexity becomes O(n2).
Correct Answer: C
Q12: Consider the following sequence of nodes for the undirected graph given below:
1. a b e f d g c
2. a b e f c g d
3. a d g e b c f
4. a d b c g e f
A Depth First Search (DFS) is started at node a. The nodes are listed in the order they are first visited. Which of the above is/are possible output(s)? (2008)
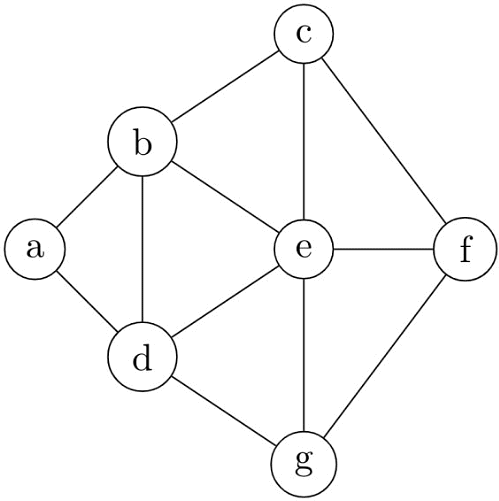
(a) 1 and 3 only
(b) 2 and 3 only
(c) 2, 3 and 4 only
(d) 1, 2 and 3 only
Ans: (b)
Sol:
1. After f is visited, c or g should be visited next. So, the traversal is incorrect.
4. After c is visited, e or f should be visited next. So, the traversal is incorrect.
2 and 3 are correct.
Q13: The Breadth First Search algorithm has been implemented using the queue data structure. One possible order of visiting the nodes of the following graph is (2008)
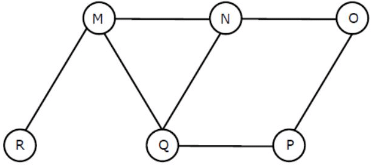
(a) MNOPQR
(b) NQMPOR
(c) QMNPRO
(d) QMNPOR
Ans: (c)
Sol:
A. MNOPQR: If you try to run BFS, after M, you must traverse NQR (In some order). Here, P is traversed before Q, which is wrong.
B. NQMPOR: This is also not BFS. P is traversed before O.
C. QMNPRO: Correct.
D. QMNPOR: Incorrect. Because R needs to be traversed before O. (Because M is ahead of N in queue).
Q14: The most efficient algorithm for finding the number of connected components in an undirected graph on n vertices and m edges has time complexity (2008)
(a) Θ(n)
(b) Θ(m)
(c) Θ(m + n)
(d) Θ(mn)
Ans: (c)
Sol: Run DFS to find connected components. Its time complexity is Θ(m + n), hence (C) is the answer.
Q15: A depth-first search is performed on a directed acyclic graph. Let d[u] denote the time at which vertex u is visited for the first time and f[u] the time at which the DFS call to the vertex u terminates. Which of the following statements is always
TRUE for all edges (u, v) in the graph? (2007)
(a) d[u] < d[v]
(b) d[u] < f[v]
(c) f[u] <f[v]
(d) f[u] > f[v]
Ans: (d)
Sol:
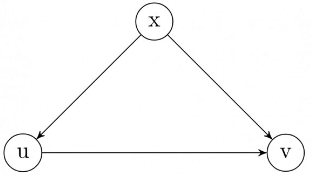
I'm gonna disprove all wrong options here:
A. d[u] < d[v], Counter Example ⇒ Well if we directly start DFS on V first, then I call DFS on X which visits U.
B. d[u] <f[v], Counter example ⇒ Same as A
C. f[u] <f[v], Counter example ⇒ Same as A again
So, answer is D.
Q16: Consider the DAG with V = {1,2,3,4,5,6}, shown below.
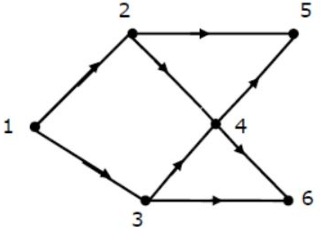
Which of the following is NOT a topological ordering? (2007)
(a) 1 2 3 4 5 6
(b) 1 3 2 4 5 6
(c) 1 3 2 4 6 5
(d) 3 2 4 1 6 5
Ans: (d)
Sol: We see that 3 cannot come at first because indegree is not 0. So, D is the answer here.
ALL other options are in Topological order.
Only 1 and 4 order matter for this question.
Q17: Consider the depth-first-search of an undirected graph with 3 vertices P, Q, and R. Let discovery time d(u) represent the time instant when the vertex u is first visited, and finish time f(u) represent the time instant when the vertex u is last visited. Given that
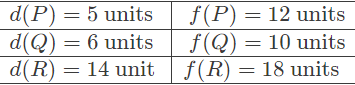
Which one of the following statements is TRUE about the graph? (2006)
(a) There is only one connected component
(b) There are two connected components, and P and R are connected
(c) There are two connected components, and Q and R are connected
(d) There are two connected components, and P and Q are connected
Ans: (d)
Sol:
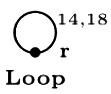
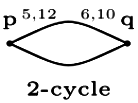
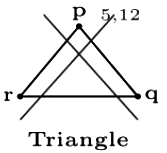
As seen in question, after 10 we have to go for p again and since p is finished and then r is started it means r must be disconnected. If there is an edge from q to r then r must be visited before q and p end.
Q18: Let T be a depth first search tree in a undirected graph G Vertices u and v are leaves of this tree T. The degrees of both u and v in G are at least 2. Which one of the following statements is true? (2006)
(a) There must exist a vertex w adjacent to both u and v in G
(b) There must exist a vertex w whose removal disconnects u and v in G
(c) There must be exist a cycle in G containing u and v
(d) There must exist a cycle in G containing u and all its neighbours in G
Ans: (d)
Sol: Let T be a depth-first search tree in an undirected graph G. Vertices u and v are leaves of this tree T. The degrees of both u and v in G are at least 2.
Let's interpret question correctly and draw inferences
Means (1) (u,v) is not an edge in the graph otherwise one would have been descendent of another and both of them must not be leaves.
(2) If vertices u and v are leaves of tree T, then when DFS was exploring them, after exploring say vertex u, it was unable to find any new unvisited Neighbour of u and hence, it had to backtrack the search. So, u became leaf of T. Same story goes with vertex v.
(3)If degrees of vertices u and v are at least 2 then I say consider the scenario for vertex u
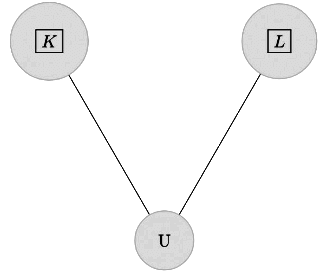
Consider some intermediate vertices K and L which are neighbours of vertex U, and there may be more vertices than K and L, ahead of them connected to either one of them(to K or L) but for simplicity, I consider only two(K and L).
Now, say my DFS algorithm explored vertex K, coloured it, Grey, then it went to vertex U and found it WHITE (means unvisited) so it marks it Grey and makes the edge (K,U) a tree edge. Now DFS examines neighbour of U and finds neighbour L.
Now if the neighbour L was WHITE (Means not visited), DFS would have visited this vertex L and then edge (U,L) would have been marked as tree edge and in this case Vertex, U would no longer be a leave in DFS Tree T.
So, Necessarily my vertex L was visited before U (L Maybe GREY or BLACK in colour) and this would have been connected to vertex K via some other vertices or directly, otherwise, it was impossible for this vertex L to be discovered via path any other than from U to L.
So, what all this means?
Yes Vertex U and it's neighbour are in a cycle and your DFS will mark some edges as back edges.
The similar story would hold for vertex V.
So, even if Option had said
"Vertex U and V are involved in cycle with their neighbour" then also this would have been true.
So Option (D) is the answer.
Q19: In a depth-first traversal of a graph G with n vertices, k edges are marked as tree edges.
The number of connected components in G is (2005)
(a) k
(b) k+1
(c) n-k-1
(d) n-k
Ans: (d)
Sol:

Tree edges are those edges which appear in the final DFS forest. For example in case of connected graph (i.e. resulting DFS forest containing only one tree), if we run DFS over it, edges belonging to the resulting DFS tree are called tree edges.
Let us assume the graph has a number of connected (or strongly connected in case of a directed graph) components. And assume 1st component has K1 tree edges, 2nd component has K2 tree edges and xth component has Kx tree edges.
Such that K1 + K2 + K3 +..+ Kx( = total)
Or in other way we can imagine like, the final DFS forest has a trees and those trees are having K1, K2, K3, ... , Kx edges respectively.
Now we know that a tree having Kx edges contains Kx + 1 nodes. Similarly a tree having K1 edges contains K1 + 1 nodes, etc. and so on.
So, summation of nodes in each tree = n
(K1 + 1) + (K2 + 1) + (K3 + 1) + ... + (Kx + 1) = n (K1 + K2 + K3 + ..
Q20: Consider the following graph
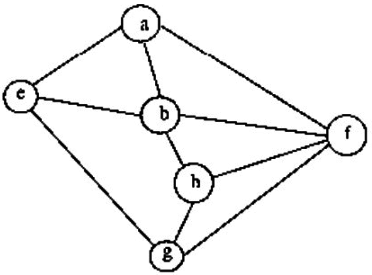
Among the following sequences
(I) a b e g h f
(II) a b f e h g
(III) a b f h g e
(IV) a f g h b e
Which are depth first traversals of the above graph? (2003)
(a) I, II and IV only
(b) I and IV only
(c) II, III and IV only
(d) I, III and IV only
Ans: (d)
Sol: For GATE purpose, without actually applying DFS, we can answer by just seeing options.
In DFS, we go in depth first i.e., one node to another in depth first order.
Here, ab f ehg is not possible as we can not go from f to e directly.
Thus, option (D) is correct.
In all the other options we can reach directly from the node to the next node.
So, just visualize and do.
Q21: Let G be an undirected graph. Consider a depth-first traversal of G, and let T be the resulting depth-first search tree. Let u be a vertex in G and let v be the first new (unvisited) vertex visited after visiting u in the traversal. Which of the following statement is always true? (2000)
(a) u, v must be an edge in G, and u is a descendant of v in T
(b) u, v must be an edge in G, and v is a descendant of u in T
(c) If u, v is not an edge in G then u is a leaf in T
(d) If u, v is not an edge in G then u and v must have the same parent in T
Ans: (c)
Sol:
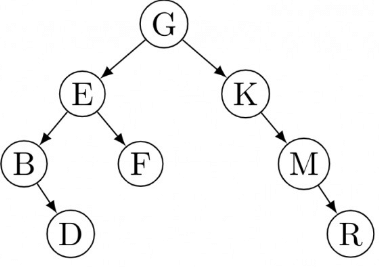
Let this be the DFS order of the tree, then,
u = D and v = F
So, we conclude that
- It is not necessary that there is an edge between them.
- If there is no edge then u must be leaf i.e. D is leaf here.
- It is not always possible that u and v have same parent. But they have same ancestor.
Correct Answer: C
Q22: Consider the undirected unweighted graph G. Let a breadth-first traversal of G be done starting from a node r.
Let d(r, u) and d(r, v) be the lengths of the shortest paths form r to u and v respectively in G. If u is visited before v during the breadth-first traversal, which of the following statements is correct? (2001)
(a) d(r, u) < d(r, v)
(b) d(r, u) ≤ d(r, v)
(c) d(r, u) > d(r, v)
(d) None of the above
Ans: (b)
Sol: The correct option is B d(r, u) ≤ d(r, v)
If u is visited before v, d(r, u) ≤ d(r, v) i.e., r to u is having shortest or equal length as compared to r to v.