Previous Year Questions: B+ Tree | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Q1: In a B+ tree, the requirement of at least half-full (50%) node occupancy is relaxed for which one of the following cases? (2024 SET 1)
(a) Only the root node
(b) All leaf nodes
(c) All internal nodes
(d) Only the leftmost leaf node
Ans: (a)
Sol: In a B+ tree, the root node serves as the entry point for accessing data in the tree. Unlike internal and leaf nodes, the root node may not have strict occupancy requirements due to its unique position and role within the tree structure. Allowing the root node to have less than half-full occupancy helps in accommodating changes in the tree's structure efficiently, especially during insertion and deletion operations. This relaxation ensures that the root node can adapt to varying data volumes and maintain a balanced tree structure. Therefore, option A, where only the root node has relaxed occupancy requirements, is the correct choice.
Q2: B+ Trees are considered BALANCED because (2016 SET 2)
(a) the lengths of the paths from the root to all leaf nodes are all equal.
(b) the lengths of the paths from the root to all leaf nodes differ from each other by at most 1.
(c) the number of children of any two non-leaf sibling nodes differ by at most 1
(d) the number of records in any two leaf nodes differ by at most 1
Ans: (a)
Sol: In B + Tree all leaves are at same level.
In both B Tree and B + trees, depth (length of root to leaf paths) of all leaf nodes is same. This is made sure by the insertion and deletion operations. In these trees, we do insertions in a way that if we have increase height of tree after insertion, we increase height from the root. This is different from BST where height increases from leaf nodes. Similarly, if we have to decrease height after deletion, we move the root one level down. This is also different from BST which shrinks from the bottom. The above ways of insertion and deletion make sure that depth of every leaf node is same.
Q3: With reference to the B+ tree index of order 1 shown below, the minimum number of nodes (including the Root node) that must be fetched in order to satisfy the following query: "Get all records with a search key greater than or equal to 7 and less than 15"is ____________. (2015 SET 2)
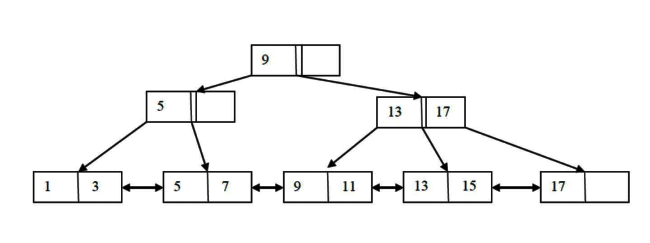
(a) 7
(b) 6
(c) 5
(d) 4
Ans: (c)
Sol: whichever way you go from the root to leaves, you'll always end up counting 5 nodes.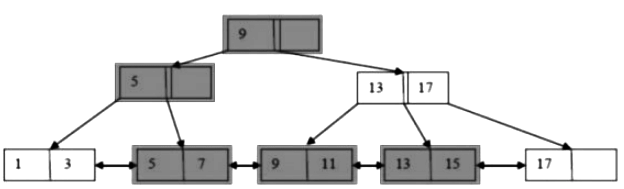
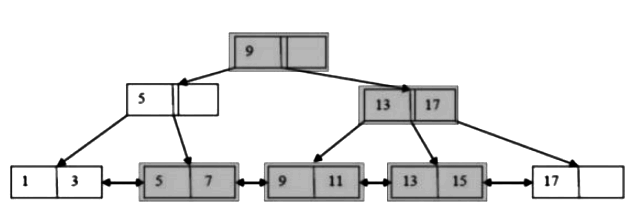


Q4: Consider a B+-tree in which the maximum number of keys in a node is 5. What is the minimum number of keys in any non-root node? (2010)
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (b)
Sol: Order = 5 + 1 = 6
Minimum children in a non root node
Keys = Minimum children in a non root node - 1 =2
Q5: The following key values are inserted into a B+ tree in which order of the internal nodes is 3, and that of the leaf nodes is 2, in the sequence given below. The order of internal nodes is the maximum number of tree pointers in each node, and the order of leaf nodes is the maximum number of data items that can be stored in it. The B+ - tree is initially empty. (2009)
10, 3, 6, 8, 4, 2, 1
The maximum number of times leaf nodes would get split up as a result of these insertions is
(a) 2
(b) 3
(c) 4
(d) 5
Ans: (c)
Sol: In this question they have asked only to count leaf node splits.
So, after discussing with my friends on Facebook, I found that you will get two different answers depending on which convention you follow. Convention 1: put the middle element in the left node, if you follow this you will get 4 as answer.
Convention 2: put the middle element in the right node, if you follow this you will get 3 as answer.
4 splits:
1. after inserting 6
2. after inserting 4
3. after inserting 2 (there will be an internal node split and a leaf node split)
4. after inserting 1
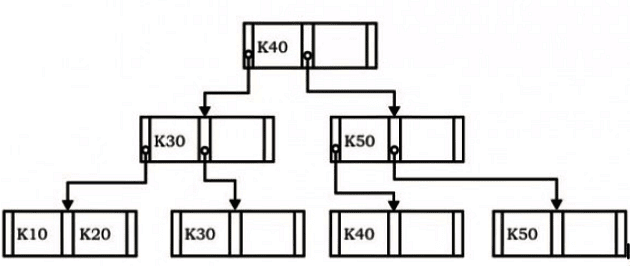
Q6: Consider the B+ tree in the adjoining figure, where each node has at most two keys and three links. (2007)
 Now the key K50 is deleted from the B + tree resulting after the two insertions made earlier. Consider the following statements about the B+tree resulting after this deletion.
Now the key K50 is deleted from the B + tree resulting after the two insertions made earlier. Consider the following statements about the B+tree resulting after this deletion.
i. The height of the tree remains the same.
ii. The node
 (disregarding the links) is present in the tree.
(disregarding the links) is present in the tree.
iii. The root node remains unchanged (disregarding the links)1
Which one of the following options is true ?
(a) Statements (i) and (ii) are true
(b) Statements (ii) and (iii) are true
(c) Statements (iii) and (i) are true
(d) All the statements are false
Ans: (a)
Sol: 
Now merge 40 in upper level.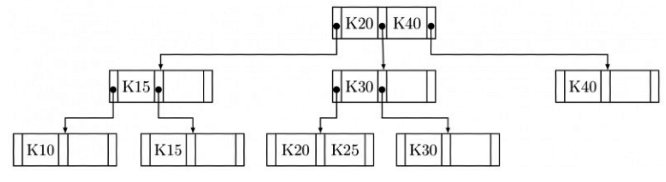 Now redistribute:
Now redistribute:
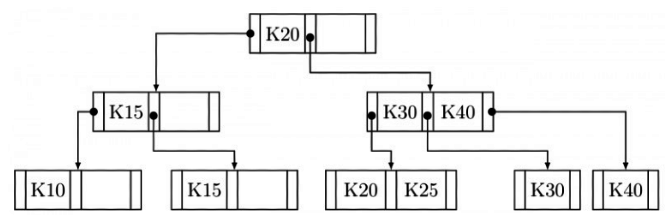
Q7: Consider the B+ tree in the adjoining figure, where each node has at most two keys and three links. (2007)
Keys K15 and then K25 are inserted into this tree in that order. Exactly how many of the following nodes (disregarding the links) will be present in the tree after the two insertions?
 (a) 1
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (a)
Sol: It is a B+ tree
After inserting K15 we get

Now, we insert K 25 , which gives - So, we see in the final tree only (K20, K25) is present.
So, we see in the final tree only (K20, K25) is present.
Q8: Which of the following is correct? (1999)
(a) B-trees are for storing data on disk and B + trees are for main memory.
(b) Range queries are faster on B+ trees.
(c) B-trees are for primary indexes and B + trees are for secondary indexes.
(d) The height of a B + tree is independent of the number of records
Ans: (a)
Sol:
A. False. Both r stored in disk
B. True. By searching leaf level linearly in B + tree, we can say a node is present or not in B + tree. But for B tree we have to traverse the whole tree
C. False. B tree and B + tree uses dynamic multilevel indexes
D. False. Height depends on number of record and also max no of keys in each node (order of tree)
|
119 docs|30 tests
|
FAQs on Previous Year Questions: B+ Tree - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is a B+ tree in computer science engineering? |  |
| 2. How does a B+ tree differ from a B tree? |  |
| 3. What are the advantages of using a B+ tree in computer science engineering? |  |
| 4. How is data insertion handled in a B+ tree? |  |
| 5. Can a B+ tree be used for disk-based storage in computer science engineering applications? |  |

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
















