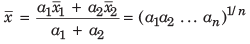Statistics | Quantitative Aptitude for SSC CGL PDF Download
| Table of contents |

|
| Mean |

|
| Median |

|
| Mode |

|
| Solved Example |

|
Statistics is the study of collection, analysis, interpretation, presentation and organisation of data. It deals with all aspects of data, including the planning of data collection in terms of design of surveys and experiments.
Mean
The mean of a set of data values is the sum of all data values divided by the number of data values.
Arithmetic Mean
The average of set of numerical values as calculated by adding them together and dividing by the number of terms in the set.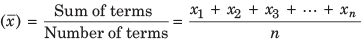
- For two numbers a and b, AM = (a +b)/2
 = 0 where x is the AM ( i = 1....n).
= 0 where x is the AM ( i = 1....n). - If
 are the respective AMs of two different sets of data having a1 and a2 elements respectively, then mean of the total set is
are the respective AMs of two different sets of data having a1 and a2 elements respectively, then mean of the total set is
Geometric Mean
For two numbers a and b, 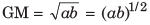
Harmonic Mean
In Mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired. The harmonic mean of the positive real numbers a1, a2 .....K an > 0 is defined to be,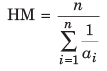
For two numbers a and b, 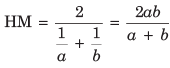
⇒ AM ≥ GM ≥ HM
Mean of Ungrouped Data
The information collected systematically regarding a population or a sample survey is called ungrouped data.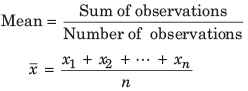
Mean of Grouped Data
If x1, x2 , . . , xn are observations with respective frequencies f1, f2,..., fn , then the mean
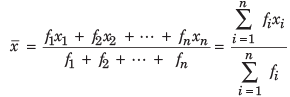
Assumed Mean Method:
Assumed mean method for calculating mean
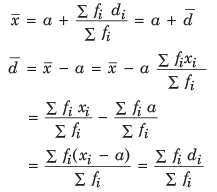
Example: The following table gives the marks scored by 24 students in a class
Find the mean of the data given.
(a) 26.81
(b) 27.91
(c) 28.11
(d) None of these
Ans: (b)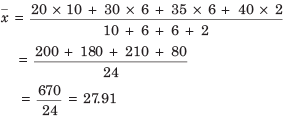
Median
When numbers are arranged either in ascending or descending order, median
- is the middle term when number of terms is odd.
- is the average of middle two terms when the number of terms is even.
- divides the distribution in two equal parts.
Median of Ungrouped Data
Step 1 We arrange the data into ascending order or descending order.
Step 2 (a) If n is an odd number, then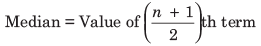
(b) If n is an even number, then Median
Here, n = 6
Median of Grouped Data
Date which have been arranged in groups or classes rather than showing all the original figures.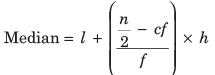
where,
l = Lower limit of median class
n = Number of observations
cf = Cumulative frequency of class preceding the median class
f = Frequency of median class
h = Class size
⇒ Find cumulative frequencies of all the classes and n / 2.
Locate the class whose cumulative frequency is greater than n /2. That is called the median class.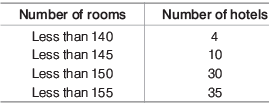
Example: The data below given shows the number of rooms in 50 hotels of a city Find the median number of rooms.
Find the median number of rooms.
(a) 148.25
(b) 148.50
(c) 148.75
(d) 149.00
Sol. (c)
Here, n = 50
So, n/2 = 25
which lies in 145 150 class interval.
∴ The modal class = 145 −150,
l = 145, cf = 10,
f = 20 and h = 5
Thus,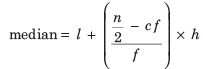
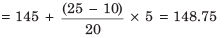
Mode
The number which has the highest frequency is the mode.
Mode of Ungrouped Data
e.g. 4, 1, 1, 4, 11, 11, 7, 5, 11, 35, 12, etc.
Here, mode is 11. e.g. 4, 4, 1, 4, 11, 11, 7, 5, 11, 35, 12, etc.
This distribution is multi-modal.
In this situation the mode will become undefined. In the cases where 2 or more items carry the same highest frequency, mode is ill-defined as a measure of central tendency. e.g. 4, 7, 1, 15, 35, 25, 18, etc.
In this case, mode is also ill-defined.
Mode of Grouped Data
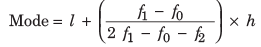
where,
l = Lower limit of the modal class (class with maximum frequency is modal class)
h = Size of the class interval
f0 = Frequency of the class preceding to the modal class
f1 = Frequency of the modal class
f2 = Frequency of the class succeeding to the modal class
Example: The table below shows the number of cars (in lakh) on road of 30 different states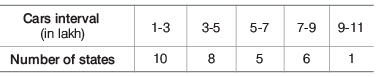
What is the mode of the data shown above?
(a) 3.66
(b) 2.66
(c) 3.00
(d) None of the above
Sol. (b)
Here, the modal class = 1-3 (as it has the maximum frequency i.e. 10)
l = 1, Class size (h) = 2 ,
f1 = 10, f0 = 0, f2 = 8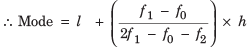
Empirical Relationship between Mean, Median and Mode
For a moderately skewed distribution, the following relationship is found to be valid
Mode = 3 Median − 2 Mean
where, skewness refers to the degree of departure from a normal i.e. bell shaped symmetrical distribution.
Example: For a given data mean is 39 and mode is 36. Find the median.
(a) 38
(b) 39
(c) 37
(d) 40
Sol. (a)
Mode = 3 Median − 2 Mean
⇒ 36 = 3 × Median − 2 × 39
⇒ 36 = 3 × Median − 78
⇒ 36 + 78 = 3 Median ⇒ 114/3 = Median
∴ Median = 38
Solved Example
Q1: Marks obtained by a student in 5 subjects are given below 25, 26, 27, 28, 29 in these obtained marks 27 is
(a) mode
(b) median and mode
(c) mean and median
(d) Both (a) and (c)
Ans: (c)
27 is in the middle, so is the median and its the mean too.
Q2: The mean weekly pay for ten persons equals to ₹ 100, if one of the persons gets a hike of `₹ 10 per week, what is the new mean weekly pay?
(a) ₹ 99
(b) ₹ 101
(c) ₹ 200
(d) ₹ 250
Ans: (b)
Total weekly salary = 100 × 10 = ₹ 1000
After hike, total salary = 1000 + 10 = ₹ 1010
Now, mean weekly salary = 1010/10 = ₹101
Q3: The mode for the following data will be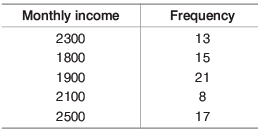 (a) 2300
(a) 2300
(b) 2500
(c) 1900
(d) 2100
Ans: (c)
1900 as it has the highest frequency.
Q4: Mean of 11 observations is 17.5. If an observation 15 is deleted, then find the mean of the remaining observations.
(a) 17.5
(b) 17.25
(c) 17.75
(d) None of these
Ans: (c)
Mean of the 11 observations is 17.5.
∴ 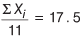
⇒ Total of 11 observations = ΣXi = 11 × 17.5
= 192.5
One observation 15 is deleted.
i.e. total of 10 observations = 192 . 5 − 15 = 177. 5
∴ Mean of 10 observations = 177.5/10 = 17.75
Q5: The median for the data 2, 4, 6, 8, 10, 12, 14 is
(a) 6
(b) 8
(c) 9.5
(d) 10
Ans: (b)
4th observation i.e. 8 is the median.
Q6: The mean of the following data is (a) 10
(a) 10
(b) 11
(c) 12
(d) None of these
Ans: (b)
The mean of the data given below: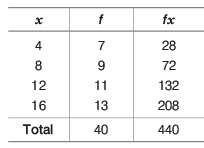
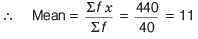
Q7: The sales in rupees of a particular soap from Sunday to Saturday are given. Find the mean of daily sales 310, 420, 380, 370, 215, 430, 270.
(a) 342
(b) 342.25
(c) 342.5
(d) None of these
Ans: (a)
Arithmetic mean,
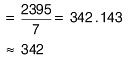
Q8: If 6, 4, 5 and 3 occur with frequencies 2, 2, 5 and 4 respectively, then the arithmetic mean is
(a) 6
(b) 4.38
(c) 6.25
(d) 5.42
Ans: (b)
Arithmetic mean,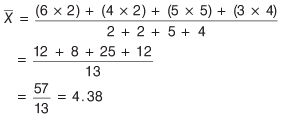
|
314 videos|170 docs|185 tests
|
FAQs on Statistics - Quantitative Aptitude for SSC CGL
| 1. What is the difference between mean, median, and mode? |  |
| 2. How are mean, median, and mode used in statistics? |  |
| 3. When is it appropriate to use the mean, median, or mode in data analysis? |  |
| 4. How do you calculate the mean, median, and mode of a set of numbers? |  |
| 5. Can a data set have more than one mode? |  |
|
314 videos|170 docs|185 tests
|

|
Explore Courses for SSC CGL exam
|

|
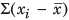 = 0 where x is the AM ( i = 1....n).
= 0 where x is the AM ( i = 1....n).  are the respective AMs of two different sets of data having a1 and a2 elements respectively, then mean of the total set is
are the respective AMs of two different sets of data having a1 and a2 elements respectively, then mean of the total set is