Previous Year Questions- Measurement of Energy and Power - 2 | Electrical and Electronic Measurements - Electrical Engineering (EE) PDF Download
Q16: The pressure coil of a dynamometer type wattmeter is (2009)
(a) Highly inductive
(b) Highly resistive
(c) Purely resistive
(d) Purely inductive
Ans: (b)
Sol: It is difficult to have purely resistive pressure coil. The pressure coil has a small value of inductance, due to which error occurs in wattmeter readings.
Q17: A sampling wattmeter (that computes power from simultaneously sampled values of voltage and current) is used to measure the average power of a load. The peak to peak voltage of the square wave is 10 V and the current is a triangular wave of 5 A p-p as shown in the figure. The period is 20 ms. The reading in W will be (2006)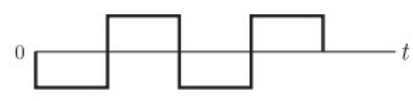
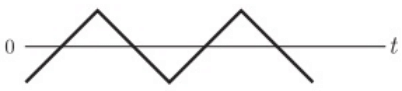 (a) 0 W
(a) 0 W
(b) 25 W
(c) 50 W
(d) 100 W
Ans: (a)
Sol:  Positive Power = Negative Power
Positive Power = Negative Power
So average power = 0 W
Q18: Two wattmeters, which are connected to measure the total power on a three-phase system supplying a balanced load, read 10.5 kW and -2.5 kW, respectively. The total power and the power factor, respectively, are (2005)
(a) 13.0 kW, 0.334
(b) 13.0 kW, 0.684
(c) 8.0 kW, 0.52
(d) 8.0 kW, 0.334
Ans: (d)
Sol: P1 = 10.5kW and P2 = −2.5kW
Total power = P1 + P2
= 10.5 − 2.5 = 8kW
Power factor,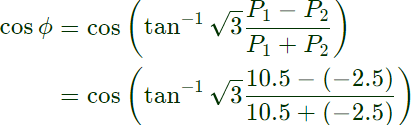 = 0.334
= 0.334
Q19: A single-phase load is connected between R and Y terminals of a 415 V, symmetrical, 3-phase, 4-wire system with phase sequence RYB. A wattmeter is connected in the system as shown in figure. The power factor of the load is 0.8 lagging. The wattmeter will read (2004)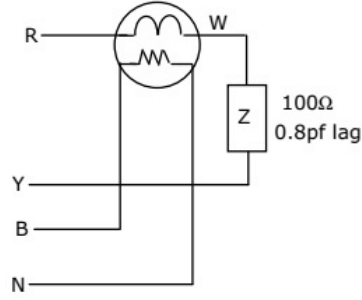 (a) −795W
(a) −795W
(b) −597W
(c) +597W
(d) +795W
Ans: (b)
Sol: Line of line voltage = 450V
Phase to neutral voltage = 415√3 V
Taking VR as the reference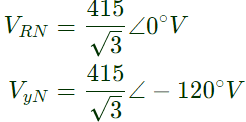 and
and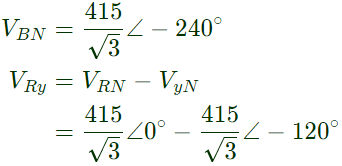 = 415∠30° V
= 415∠30° V
Load current,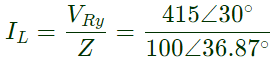 = 4.15∠-6.87° A
= 4.15∠-6.87° A
Current through current coil,
Icc = IL = 4.15∠ − 6.87° A
Voltage across pressure coil
VBN = 4.15/√3 ∠ − 240° V
Phase angle between VBN and Icc
ϕ = −240°−(−6.87°) = 233.13°
Wattmeter reading = ∣VBN∣∣IL∣cosϕ
= (415/√3) x 4.15 x cos 233.13
= -597 W
Q20: A dc A-h meter is rated for 15 A, 250 V. The meter constant is 14.4 A-sec/rev. The meter constant at rated voltage may be expressed as (2004)
(a) 3750 rev/kWh
(b) 3600 rev/kwh
(c) 1000 rev/kWh
(d) 960 rev/kWh
Ans: (c)
Sol: Meter constant , m = 14.4 A-sec/rev
To express meter constant in the unit rev/kWh
Meter constant 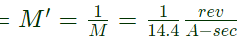
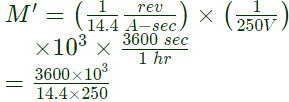 = 1000 rev/kWh
= 1000 rev/kWh
Q21: The circuit in figure is used to measure the power consumed by the load. The current coil and the voltage coil of the wattmeter have 0.02 Ω and 1000 Ω resistances respectively. The measured power compared to the load power will be (2004) (a) 0.4 % less
(a) 0.4 % less
(b) 0.2% less
(c) 0.2% more
(d) 0.4% more
Ans: (c)
Sol: Load Power (true power) = V I cosϕ
= 200 × 20 × 1 = 4000W
Resistance of current coil = Rcc = 0.02
Current through CC = Ic = 20A
Power consumed by current coil
= I2cRcc
= 202 × 0.02 = 8W
Measured power = Power consumed by load + Power consumed by current coil
Measured power = 4000 + 8 = 4008W
%error = 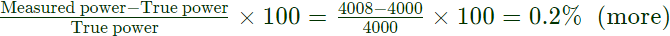
Q22: The voltage-flux adjustment of a certain 1-phase 220 V induction watt-hour meter is altered so that the phase angle between the applied voltage and the flux due to it is 85° (instead of 90°). The errors introduced in the reading of this meter when the current is 5 A at power factor of unity and 0.5 lagging are respectively (2003)
(a) 3.8 mW, 77.4 mW
(b) -3.8 mW, 77.4 mW
(c) -4.2 W, -85.1 W
(d) 4.2 W, 85.1 W
Ans: (c)
Sol: Measured value = V I sin(Δ − ϕ)
where,
Δ = Phase angle between voltage and flux
cosϕ = Poer factor
True value = VIcosϕ
Error = Measured value - True value
CASE-I:
Δ = 80°
pf = cosϕ = 1
ϕ = 0°
V = 220 V
I = 5 A
Error = VI sin(Δ - ϕ) - VI cosϕ
= 220 x 5sin(85 - 0°) - 220 x 1 x 1
≈ -4.2 W
CASE-II:
Δ = 85°
pf = cosϕ = 0.5
ϕ = 60°
V = 220 V
I = 5A
Error = VI sin(Δ - ϕ) - VI cosϕ
= 220 x 5sin(85 - 60°) - 220 x 5 x 0.5
= -85.1 W
Q23: A wattmeter reads 400 W when its current coil is connected in the R-phase and its pressure coil is connected between this phase and the neutral of a symmetrical 3-phase system supplying a balanced star connected 0.8 p.f. inductive load. This phase sequence is RYB. What will be the reading of this wattmeter if its pressure coil alone is reconnected between the B and Y phases, all other connections remaining as before ? (2003)
(a) 400
(b) 519.6
(c) 300
(d) 692.8
Ans: (b)
Sol: Taking VR as the reference and assuming phase to neutral voltage = V
VR = V∠0°
VY = V∠−120°
and VB = V ∠−240° VRIRcosϕ = 400 W
VRIRcosϕ = 400 W
VIR × 0.8 = 400 W
VIR = 400 ...(i)
IR = IR∠ -36.87°
[p.f. = 0.8 lag, inductive load]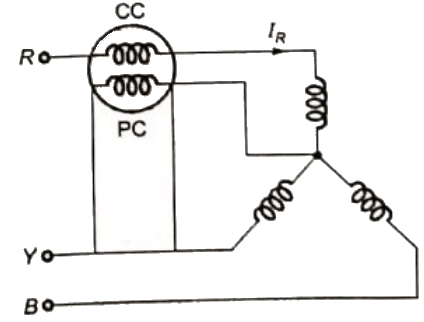 VYB = VYB - VB
VYB = VYB - VB
= V∠ −120° − V ∠ − 240°
= √3V ∠ -90° V
IR = IR∠ -36.87° A
Angle between VYB and IR
θ = −90° − (−36.87°) = 53.13°
As pressure coil connected between Y and B phase.
Reading of wattmeter = VYBIRcosθ
From equation (i)
= √3V × IR × cos(−53.13) = √3 × 500 × 0.6 = 519.6W
Q24: The line-to-line input voltage to the 3 phase, 50 Hz, ac circuit shown in figure is 100 V rms. Assuming that the phase sequence is RYB, the wattmeters would read. (2002)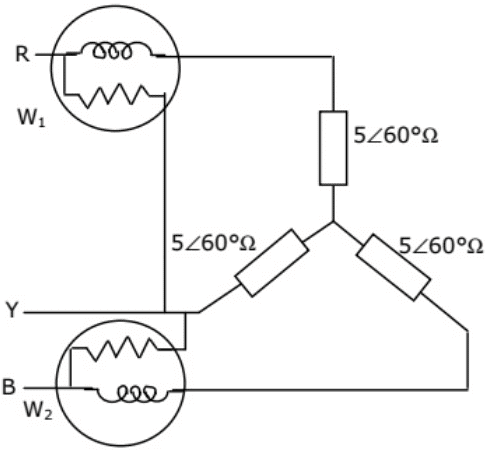 (a) W1 = 886 W and W2 = 886 W
(a) W1 = 886 W and W2 = 886 W
(b) W1 = 500 W and W2 = 500 W
(c) W1 = 0 W and W2 = 1000 W
(d) W1 = 250 W and W2 = 750 W
Ans: (c)
Sol: VL = 100V
IL = IP = VP/Z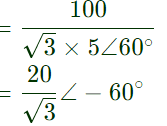 W1 = VLILcos(30° − ϕ)
W1 = VLILcos(30° − ϕ)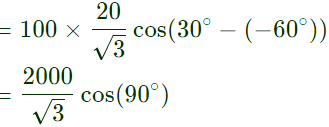 W2 = VLILcos(30° + ϕ)
W2 = VLILcos(30° + ϕ)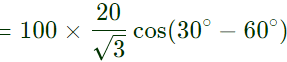 = 1000W
= 1000W
Q25: The minimum number of wattmeter (s) required to measure 3-phase, 3-wire balanced or unbalanced power is (2001)
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (b)
Sol: Two wattmeter method can also take care of unbalance.
Q26: If an energy meter disc makes 10 revolutions in 100 seconds when a load of 450 W is connected to it, the meter constant (in rev/kWh) is (2001)
(a) 1000
(b) 500
(c) 1600
(d) 800
Ans: (d)
|
3 videos|39 docs|22 tests
|
|
3 videos|39 docs|22 tests
|

|
Explore Courses for Electrical Engineering (EE) exam
|

|
















