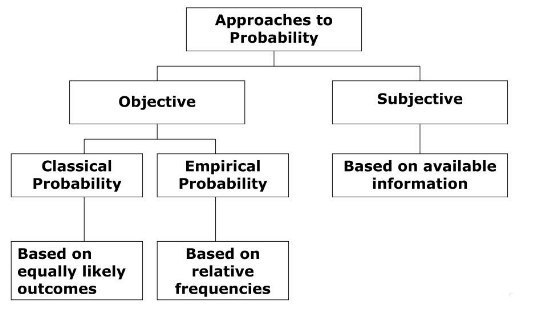
Approaches to Probability | UGC NET Commerce Preparation Course PDF Download
Classical or Mathematical Definition of Probability
Consider an experiment that can result in m+n possible outcomes, which are equally likely, mutually exclusive, and exhaustive. Out of these, m outcomes are favorable to event A, while the remaining n outcomes are not favorable. The probability of event A is defined as the ratio of the number of favorable outcomes to the total number of possible outcomes.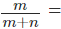

The probability of the occurrence of the event ‘A’ is P(A). Further, P(A) always lies between 0 and 1. These are the limits of probability.
Instead of saying that the probability of the occurrence of the event ‘A’ is  we can say that “Odds are m to n in favor of event A or n to m against the event A.”
we can say that “Odds are m to n in favor of event A or n to m against the event A.”
Therefore,
Odds in favor of the event A  =
= 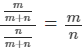
Odds against the event A 
Note: The ratio m/n or n/m is always expressed in its lowest form (integers with no common factors).
- If m = 0, or if the number of cases favorable to the occurrence of the event A = 0 then, P(A) = 0. In other words, event A is an impossible event.
- If n = m, then P(A) = m/m = 1. This means that the event A is a certain or sure event.
- If neither m = 0 nor n = 0, then the probability of occurrence of any event A is always less than 1. Therefore, the probability of occurrence the event satisfies the relation 0 < P < 1.
If the events are mutually exclusive and exhaustive, then the sum of their individual probabilities of occurrence = 1.
For example, if A, B, and C are three mutually exclusive events, then P(A) + P(B) + P(C) = 1. The probability of the occurrence of one particular event is the Marginal Probability of that event.
Choosing an object at random from N objects means that each object has the same probability 1/N of being chosen.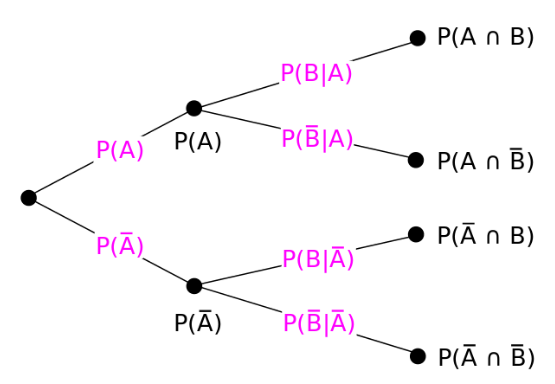
Empirical Probability or Relative Frequency Probability Theory
The Relative Frequency Probability Theory is as follows:
We can define the probability of an event as the relative frequency with which it occurs in an indefinitely large number of trials. Therefore, if an event occurs ‘a’ times out of ‘n’, then its relative frequency is a/n.
Further, the value that a/n approaches when ‘n’ becomes infinity is the limit of the relative frequency.
Symbolically,
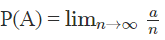
However, in practice, we write the estimate of P(A) as follows:
P(A) = a/n
While the classical probability is normally encountered in problems dealing with games of chance. On the other hand, the empirical probability is the probability derived from past experience and is used in many practical problems.
Total Probability Theorem or the Addition Rule of Probability
If A and B are two events, then the probability that at least one of then occurs is P(A∪B). We also have,
P(A∪B) = P(A) + P(B) – P(A∩B)
If the two events are mutually exclusive, then P(A∩B) = 0. In such cases, P(A∪B) = P(A) + P(B).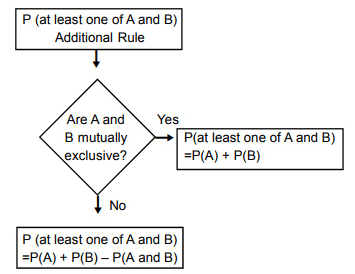
Multiplication Rule
If A and B are two events, the probability of their joint or simultaneous occurrence is:
P(A∩B) = P(A) . P(A/B)
If the events are independent, then
- P(A/B) = P(A)
- P(B/A) = P(B)

Therefore, we now have,
If the events are independent, then P(A∪B) = P(A) + P(B) – P(A∩B)
Also, P(A/B) is the conditional probability of the occurrence of the event A when event B has already occurred. Similarly, P(B/A) is the conditional probability of the occurrence of event B when event A has already occurred. If the events are independent, then the occurrence of A does not affect the occurrence of B.
∴ P(B/A) = P(B)
Also, P(A/B) = P(A)
Solved Example
Example 1: The percentages of 100 teenage offenders are in the following six categories: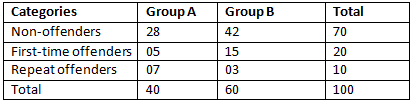
If you choose a teenager at random, then the following events are defined:
- The teenager is from Group A
- The teenager is from Group B
- The teenager is not an offender
Find the following probabilities:
- P(A)
- P(B)
- P(C)
Sol:
The probability that a teenager is from Group A is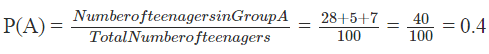
The probability that a teenager is from Group B is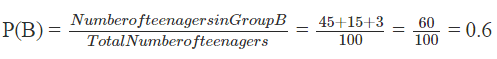
The probability that a teenager is from Group C is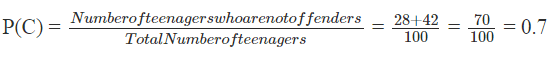
Example 2: An analyst develops the following table of joint probabilities relating the size of firm (measured in terms of the number of employees) and the type of firm.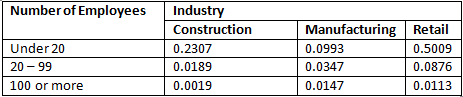
If one is selected at random, find the probability of the following events:
(i) P(A) = The firm employs fewer than 20 employees
(ii) P(B) = The firm is in the retail
(iii) P(C) = A firm in the construction industry employs between 20 to 99 workers
(iv) P(D) = A firm in the retail industry employed more than 20 workers.
Sol:
(i) The firm employs fewer than 20 employees
P(A) = 0.2307 + 0.0993 + 0.5009 = 0.8303
(ii) The firm is in the retail
P(B) = 0.5009 + 0.0876 + 0.0113 = 0.5998
(iii) A firm in the construction industry employs between 20 to 99 workers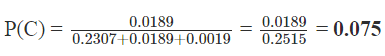
(iv) A firm in the retail industry employed more than 20 workers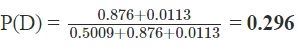
|
235 docs|166 tests
|
FAQs on Approaches to Probability - UGC NET Commerce Preparation Course
| 1. What are the different approaches to probability in the context of UGC NET? |  |
| 2. How is classical or theoretical probability defined in the UGC NET? |  |
| 3. What is empirical or experimental probability as per the UGC NET syllabus? |  |
| 4. How is subjective probability explained in the UGC NET context? |  |
| 5. What is axiomatic probability and its relevance to UGC NET? |  |

|
Explore Courses for UGC NET exam
|

|
















