Number Play NCERT Solutions | Mathematics for Class 6 PDF Download
| Table of contents |

|
| Page 55 |

|
| Page 56 |

|
| Page 57 & 58 |

|
| Page 59 |

|
| Page 60 |

|
| Page 61 |

|
| Page 62 |

|
| Page 63 |

|
| Page 64 & 65 |

|
| Page 66 & 67 |

|
| Page 69 & 70 |

|
| Page 71 |

|
| Page 72 |

|
| Page 73 |

|
Page 55
Q1: Think about various situations where we use numbers. List five different situations in which numbers are used. See what your classmates have listed, share, and discuss.
Ans:
Five different situations where we use numbers:
1. While telling the time, we use numbers to check hours and minutes on a clock.
2. When we go shopping, we use numbers to see the prices of items and calculate the total cost.
3. In sports, numbers are used to keep score, like goals in football or runs in cricket.
4. While measuring height or weight, numbers tell us how tall or heavy someone is.
5. In school, numbers are used for marks in exams or assignments.
Q2. Some children in a park are standing in a line. Each one says a number.
A child says '1' if there is only one taller child standing next to them. A child says '2' if both the children standing next to them are taller. A child says '0', if neither of the children standing next to them are taller. That is each person says the number of taller neighbours they have.
What do you think these numbers mean?
Ans: These numbers mean the number of taller children near that child.
Page 56
A child says '1' if there is only one taller child standing next to them. A child says '2' if both the children standing next to them are taller. A child says '0', if neither of the children standing next to them are taller. That is each person says the number of taller neighbours they have.
Try answering the questions below and share your reasoning:
Q1: Can the children rearrange themselves so that the children standing at the ends say ‘2’?
Ans: Yes, the children can rearrange themselves so that the children at the ends say ‘2’ because, as the line given above in the paragraph states, A child says '2' if both the children standing next to them are taller.
 Q2: Can we arrange the children in a line so that all would say only 0s?
Q2: Can we arrange the children in a line so that all would say only 0s?
Ans: Yes, it is possible to arrange the children in a line where all of them say only 0s. because, as the line given in the paragraph states, A child says '0', if neither of the children standing next to them is taller. That is, each person says the number of taller neighbours they have.
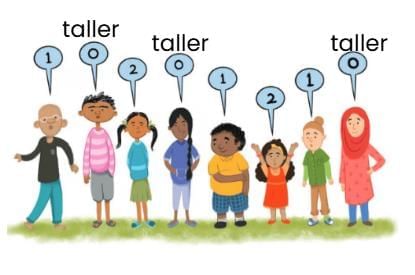 Q3: Can two children standing next to each other say the same number?
Q3: Can two children standing next to each other say the same number?
Ans: Yes, two children standing next to each other can say the same number if they are arranged either in ascending or descending order of their heights.

Q4: There are 5 children in a group, all of different heights. Can they stand such that four of them say ‘1’ and the last one says ‘0’? Why or why not?
Ans: Yes, it's possible only if the 5 children are arranged in ascending order of their heights.

Q5: For this group of 5 children, is the sequence 1, 1, 1, 1, 1 possible?
Ans: No, the sequence 1,1,1,1,1 is not possible because there are only five children and at least one child must have no taller neighbours, meaning they would say 'O'. It's impossible for every child to have one taller neighbour.
Q6: Is the sequence 0, 1, 2, 1, 0 possible? Why or why not?
Ans: Yes, it is possible if the shortest child is in the middle, with the heights increasing symmetrically as you move outward from the centre.
Q7: How would you rearrange the five children so that the maximum number of children say ‘2’?
Ans: Yes, it is possible if the tall and short children arrange themselves alternately.
Page 57 & 58
Q1: Colour or mark the supercells in the table below. Ans:
Ans: 
Q2: Fill the table below with only 4-digit numbers such that the supercells are exactly the coloured cells. Ans:
Ans: 
Q3: Fill the table below such that we get as many supercells as possible. Use numbers between 100 and 1000 without repetition. Ans:
Ans: 
Q4: Out of the 9 numbers, how many supercells are there in the table above?
Ans: Out of 9 numbers, there are 5 supercells in the above table.
Q5: Find out how many supercells are possible for different numbers of cells. Do you notice any pattern? What is the method to fill a given table to get the maximum number of supercells? Explore and share your strategy.
Ans: If there are n odd cells then number of supercells = 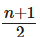
If there are n even cells then number of supercells = n/2
Yes, there is a pattern. Alternate cells can be supercells.
Method to fill a given table to get the maximum number of supercells.
- Make the first cell a supercell. After that, each alternate cell is to be made a supercell.
- No consecutive cells can be supercells except in the case of 4 cells, because then the first and fourth cells can be supercells.
For example - 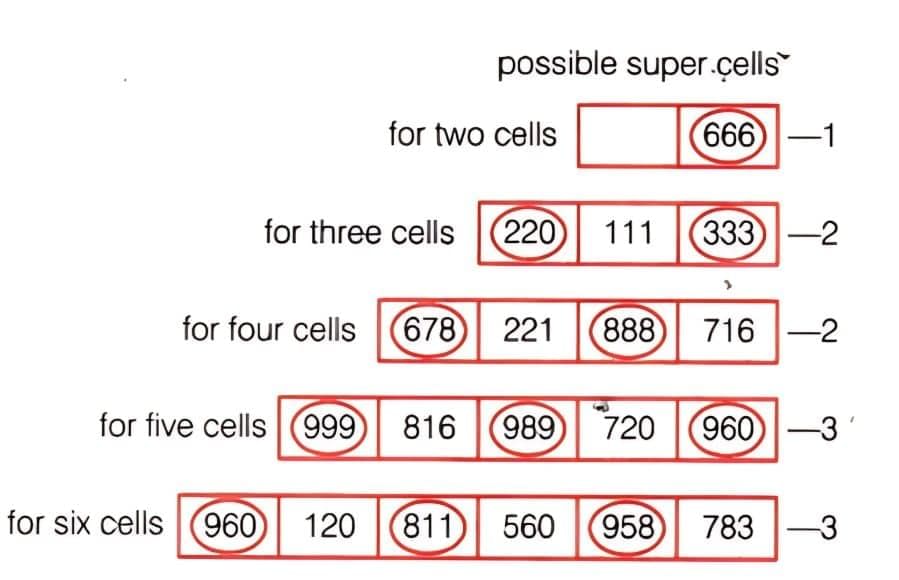
Q6: Can you fill a supercell table without repeating numbers such that there are no supercells? Why or why not?
Ans: No, it is not possible to fill a supercell table without repeating numbers such that there are no supercells.
As there are two cases:
Case I: If we fill the cells in descending order, then the first cell is the supercell.
Case II: If we fill the cells in ascending order, then the last cell will be the supercell.
If we don’t follow any order, then there will definitely at least one supercell.
Q7: Will the cell having the largest number in a table always be a supercell? Can the cell having the smallest number in a table be a supercell? Why or why not?
Ans: Yes, the cell with the largest number in a table will always be a supercell. Since the largest number is greater than any other number in the table, it will naturally be greater than its adjacent numbers. Therefore, it will always be a supercell.
No, the cell with the smallest number in a table cannot be a supercell. Since the smallest number in the table is less than or equal to all other numbers, it cannot be greater than its adjacent numbers. Thus, it cannot be a supercell.
Q8: Fill a table such that the cell having the second largest number is not a supercell.
Ans:  Largest number = 850
Largest number = 850
Second largest number = 730
Q9: Fill a table such that the cell having the second largest number is not a supercell but the second smallest number is a supercell. Is it possible?
Ans: Yes, it is possible. Here is one possible arrangement: Largest number = 750
Largest number = 750
Second largest number = 640
Smallest number = 100
Second smallest number = 210
Q10: Make other variations of this puzzle and challenge your classmates.
Ans: Fill a table such that only even numbers are supercell.
Fill a table such that all the supercells are divisible by 5.
Complete Table 2 with 5-digit numbers whose digits are ‘1’, ‘0’, ‘6’, ‘3’, and ‘9’ in some order. Only a coloured cell should have a number greater than all its neighbours.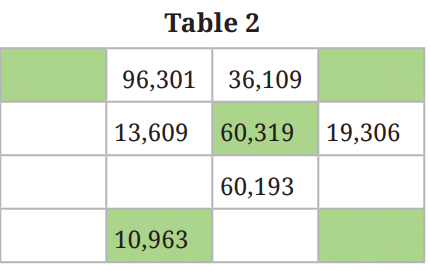
The biggest number in the table is ____________ .
The smallest even number in the table is ____________.
The smallest number greater than 50,000 in the table is ____________.
Once you have filled the table above, put commas appropriately after the thousands digit.
Ans:
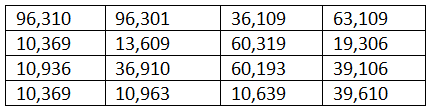
- The biggest number in the table is 96, 310.
- The smallest even number in the table is 10,936.
- The smallest number greater than 50,000 in the table is 60,193.
Page 59
Figure it Out
Q1: Identify the numbers marked on the number lines below, and label the remaining positions.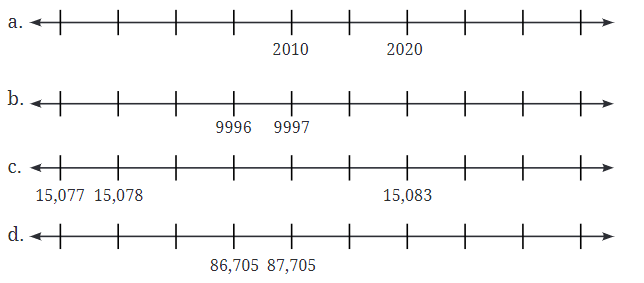 Put a circle around the smallest number and a box around the largest number in each of the sequences above.
Put a circle around the smallest number and a box around the largest number in each of the sequences above.
Ans: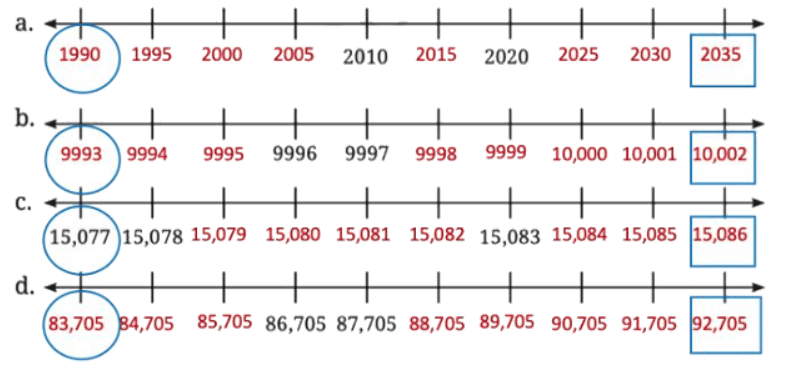
Page 60
Q1: Find out how many numbers have two digits, three digits, four digits, and five digits.

Ans:

Q2: Digit sum 14
(a) Write other numbers whose digits add up to 14.
(b) What is the smallest number whose digit sum is 14?
(c) What is the largest 5-digit whose digit sum is 14?
(d) How big a number can you form having the digit sum 14? Can you make an even bigger number?
Ans: (a) Some numbers whose digits add up to 14 are:
59, 68, 77, 86, 95, 149, 158, 167, 176, 185, 194, 239, 248, 257, 266, 275, 281, 293
(b) The smallest number whose digit sum is 14 = 59.
(c) The largest 5-digit number containing 0 whose digit sum is 14 = 95,000.
The largest 5-digit number not containing 0 whose digit sum is 14 = 92,111.
(d) Infinite numbers can be formed having the digit sum 14.
Yes, we can make a bigger even number.
Q3: Find out the digit sums of all the numbers from 40 to 70. Share your observations with the class.
Ans: 
Observation:
From 40 to 49: The digit sum increased from 4 to 13
From 50 to 59: The digit sum increased from 5 to 14
From 60 to 69: The digit sum increased from 6 to 15
From 70 to 79: The digit sum will increase from 7 to 16
Q4: Calculate the digit sums of 3-digit numbers whose digits are consecutive (for example, 345). Do you see a pattern? Will this pattern continue?
Ans:
 1 + 2 + 3 = 6,
1 + 2 + 3 = 6,
2 + 3 + 4 = 9,
3 + 4 + 5= 12,
4 + 5 + 6 = 15,
5 + 6 + 7 = 18,
6 + 7 + 8 = 21,
7 + 8 + 9 = 24.
Yes, the pattern is a table of 3 from 3 × 2 to 3 × 8.
We cannot continue this pattern after 789.
Page 61
Q1: Among the numbers 1-100, how many times will the digit ‘7’occur?
Ans: The total count of 7 that we get is 20.
Q2: Among the numbers 1-1000, how many times will the digit ‘7’occur?
Ans: The number of times 7 will be written when listing the numbers from 1 to 1000 is 300.
Q3: Write all possible 3-digit palindromes using these digits.
Ans:
- 111
- 121
- 131
- 212
- 222
- 232
- 313
- 323
- 333
Page 62
Q1: Will reversing and adding numbers repeatedly, starting with a 2-digit number, always give a palindrome? Explore and find out.
Ans: All two-digit numbers eventually become palindromes after repeated reversal and addition. About 80% of all numbers under 10,000 resolve into a palindrome ip four or fewer steps; about 90% of those resolve in seven steps or fewer.
Example 1: Number 12
1. Initial Number: 12
2. Reverse: 21
3. Add: 12 + 21 = 33
4. Palindrome
Check: 33 is a palindrome.
• Result: 33 is a palindrome.
Example 2: Number 89
1. Initial Number: 89
2. Reverse: 98
3. Add: 89 + 98 = 187
4. Palindrome Check: 187 is not a palindrome.
5. Reverse 187: 781
6. Add: 187 + 781 =968
7. Palindrome Check: 968 is not a palindrome.
Puzzle time
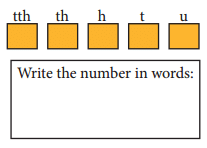
I am a 5-digit palindrome.
I am an odd number.
My ‘t’ digit is double of my ‘u’ digit.
My ‘h’ digit is double of my ‘t’ digit.
Who am I?___________
Ans: 12421
Page 63
Explore
Take different 4-digit numbers and try carrying out these steps. Find out what happens.
Ans: Selected a 4-digit number 1234
- Starting number: 1234
- Descending order: 4321
- Ascending order: 1234
- Subtract: 4321 – 1234 = 3087
Repeat:
- Descending order of 3087: 8730
- Ascending order of 3087: 0378
- Subtract: 8730 – 0378 = 8352
Repeat:
- Descending order of 8352: 8532
- Ascending order of 8352: 2358
- Subtract: 8532 – 2358 = 6174
Result: 6174 (Kaprekar constant)
Carry out these same steps with a few 3-digit numbers. What number will start repeating?
Ans: We will do this with help of two examples:
1. Number 123
- Starting number: 123
- Descending order: 321
- Ascending order: 123
- Subtract: 321 – 123 = 198
Repeat:
- Descending order of 198: 981
- Ascending order of 198: 189
- Subtract: 981 – 189 = 792
Repeat:
- Descending order of 792: 972
- Ascending order of 792: 279
- Subtract: 972 – 279 = 693
Repeat:
- Descending order of 693: 963
- Ascending order of 693: 369
- Subtract: 963 – 369 = 594
Repeat:
- Descending order of 594: 954
- Ascending order of 594: 459
- Subtract: 954 – 459 = 495
Repeat:
- Descending order of 495: 954
- Ascending order of 495: 459
- Subtract: 954 – 459 = 495
Result: The number 495 starts repeating.
2. Now let’s take the number 317
- Starting number: 317
- Descending order: 731
- Ascending order: 137
- Subtract: 731 – 137 = 594
Repeat:
- Descending order of 594: 954
- Ascending order of 594: 459
- Subtract: 954 – 459 = 495
Repeat:
- Descending order of 495: 954
- Ascending order of 495: 459
- Subtract: 954 – 459 = 495
Result: The number 495 starts repeating. When applying Kaprekar’s routine to 3- digit numbers, the number 495 is often reached and starts repeating. This number is known as the Kaprekar constant for 3-digit numbers.
Page 64 & 65
Try and find out all possible times on a 12-hour clock of each of these types. For example, 4:44, 10:10, 12:21.
Ans: 01:10, 02:20, 03:30, 04:40, 05:50, 10:01, 11:11, 12:21
Find some other dates of this form from the past like 20/12/2012 where the digits ‘2’, ‘0’, ‘1 ’, and ‘2 ’ repeat in that order.
Ans: 11/02/2011, 22/02/2022, 01/10/2010, 10/01/2010, 02/02/2020
Figure it Out
1. Pratibha uses the digits '4', '7', '3' and '2', and makes the smallest and largest 4-digit numbers with them: 2347 and 7432. The difference between these two numbers is 7432 - 2347 = 5085. The sum of these two numbers is 9779. Choose 4-digits to make:
(a) the difference between the largest and smallest numbers greater than 5085.
(b) the difference between the largest and smallest numbers less than 5085.
(c) the sum of the largest and smallest numbers greater than 9779.
(d) the sum of the largest and smallest numbers less than 9779.
Ans: (a) Digits: 9, 6, 5, 3
Largest number = 9653
Smallest number = 3569
Difference = 9653-3569 = 6084.
(b) Digits: 4, 6, 3, 2
Largest 4-digit number: 6432
Smallest 4- digit number = 2346
Difference: 6432 – 2346 = 4086 < 5085
(c) Digits: 9, 8, 7, 1
Largest number = 9871
Smallest number = 1789
Sum = 9871 +1789 = 11660
(d) Digits: 8, 5, 2, 1
Largest number = 8321
Smallest number = 1238
Sum = 8321 + 1238 = 9559
Q2: What is the sum of the smallest and largest 5-digit palindrome? What is their difference?
Ans: The smallest 5-digit palindrome = 10001
The largest 5-digit palindrome = 99999
Sum = 10001 + 99999 = 110000
Difference = 99999 - 10001 = 89998
Q3: The time now is 10:01. How many minutes until the clock shows the next palindromic time? What about the one after that?
Ans: Prime time = 10:01
Next palindromic time after 10:01 = 11:11
Difference = 11:11-10:01 = 70 minutes
Thus, the next palindromic time shows after 70 minutes.
Next palindromic time after 11 : 11=12:21
Difference = 12:21 – 11:11 = 70 minutes
= 1 hour 10 minutes
Thus, the next palindromic time shows after 1 hour 10 minutes and next one is 12 : 21 which comes total 2 hours 20 minutes later.
Q4: How many rounds does the number 5683 take to reach the Kaprekar constant?
Ans: The given number is 5683
1st round
Largest number = 8653
Smallest Number = 3568
Subtract = 8653 - 3568
= 5085
2nd round
Largest number = 8550
Smallest number = 0558
Subtract = 8550 - 0558
= 7992
3rd round
Largest number = 9972
Smallest number = 2799
Subtract= 9972 - 2799 = 7173
4th round
Largest number = 7731
Smallest number = 1377
Subtract = 7731 - 1377 = 6354
5th round
Largest number = 6543
Smallest number = 3456
Subtract = 6543 - 3456 = 3087
6th round
Largest number = 8730
Smallest number = 0378
Difference = 8730 - 0378
= 8352
7th round
Largest number = 8532
Smallest number = 2358
Difference = 8532-2358
= 6174
Therefore, the number 5683 takes 7 rounds to reach 6174 which is the Kaprekar constant.
Page 66 & 67
Q1: Write an example for each of the below scenarios whenever possible. Could you find examples for all the cases? If not, think and discuss what could be the reason. Make other such questions and challenge your classmates.
Could you find examples for all the cases? If not, think and discuss what could be the reason. Make other such questions and challenge your classmates.
Ans: 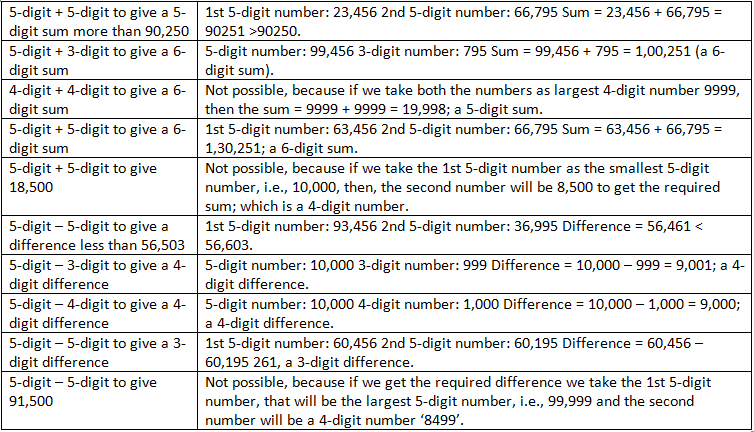
Q2: Always, Sometimes, Never?
Below are some statements. Think, explore and find out if each of the statement is 'Always true', 'Only sometimes true' or 'Never true'. Why do you think so? Write your reasoning; discuss this with the class.
(a) 5-digit number + 5-digit number gives a 5-digit number
(b) 4-digit number + 2-digit number gives a 4-digit number
(c) 4-digit number + 2-digit number gives a 6-digit number
(d) 5-digit number — 5-digit number gives a 5-digit number
(e) 5-digit number — 2-digit number gives a 3-digit number
Ans:
(a) Only sometimes true.
The given statement is ‘5-digit number + 5-digit number gives a 5-digit number’. It is only sometimes true.
e.g. 10000 +10000 = 20000 i.e. 5-digit number
and 99999 + 99999 = 199998 i.e. 6-digit number
(b) The given statement is ‘4-digit number + 2-digit number gives a 4-digit number’. It is only sometimes true.
e.g. 1000 +10 = 1010 i.e. 4-digit number
and 9999 +10 = 10009 i.e. 5-digit number
(c) The given statement is ‘4-digit number + 2-digit number gives a 6-digit number’. It is never true.
e.g. 9999 + 99 = 10098 i.e. 5-digit number
(d) The given statement is ‘5-digit number – 5-digit number gives a 5-digit number’.
It is only sometimes true.
e.g. 99999 -10000 = 89999 i.e. 5-digit number
and 98765 – 94321 = 4444 i.e. 4-digit number
(e) The given statement is ‘5-digit number – 2-digit number gives a 3-digit number’. It is never true,
e.g. 10000 – 99 = 9901 i.e. 4-digit number.
Q3: Find out the sum of the numbers in each of the below figures. Should we add them one by one or can we use a quicker way? Share and discuss in class the different methods each of you used to solve these questions.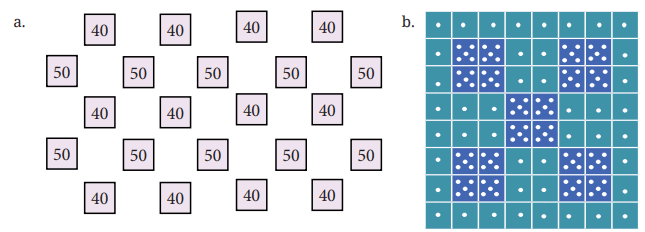
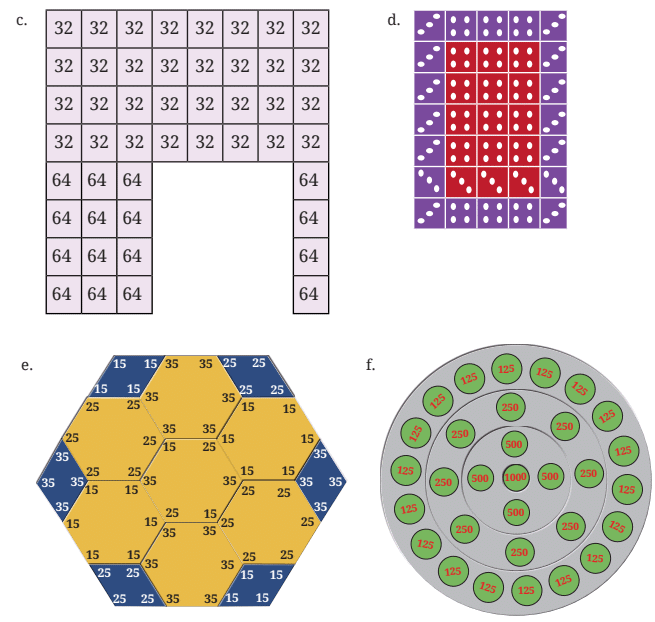
Ans: (a) In figure (a), number 40 is repeated 12 times and number 50 is repeated 10 times
Hence sum of all numbers = 40 × 12 + 50 × 10
= 480 + 500 = 980
(b) In figure (b), 1 dot (•) is 44 times and 5 dots (•) are 20 times
Hence sum of all dots = 1 × 44 + 5 × 20 = 44 + 100 = 144
(c) In figure (c), number 32 is 32 times and number 64 is 16 times
Hence sum of all numbers = 32 × 32 + 64 × 16 = 1024 + 1024 = 2048
(d) In figure (d), 3 dots (•) are 17 times and 4 dots (•) are 18 times
Hence sum of all dots = 17 × 3 + 18 × 4 = 51 + 72 = 123
(e) In figure (e), number 15 is 22 times, number 25 is 22 times and number 35 is 22 times
Hence sum of all numbers = 15 × 22 + 25 × 22 + 35 × 22 = 330 + 550 + 770 = 1650
(f) In figure (f), number 125 is 18 times, number 250 is 8 times and number 500 is 4 times and number 1000 is one time.
Hence sum of all numbers = 125 × 18 + 250 × 8 + 500 × 4 + 1000 = 2250 + 2000 + 2000 +1000 = 7250
Page 69 & 70
Figure it Out
We shall do some simple estimates. It is a fun exercise, and you may find it amusing to know the various numbers around us. Remember, we are not interested in the exact numbers for the following questions. Share your methods of estimation with the class.
Q1: Steps you would take to walk:
(a) From the place you are sitting to the classroom door
(b) Across the school ground from start to end
(c) From your classroom door to the school gate
(d) From your school to your home
Ans: (a) 35 steps.
(b) 600 steps.
(c) 400 steps.
(d) 10,000 steps.
Q2. Number of times you blink your eyes or number of breaths you take:
(a) In a minute
(b) In an hour
(c) In a day
Ans: (a) 20 times
(b) No. of times eyes blink in a minute = 20
No. of minutes in a hour = 60 minutes
No. of times eyes blink in an hour = 20 x 60 = 1200.
(c) No. of times eyes blink in an hour = 1200
No. of hours in a day = 24 hours
No. of hours we sleep in a day = 7 hours
No of times eyes blink in a day = (24 - 7) x 1200
= 17 x 1200
= 20,400
Q3: Name some objects around you that are:
(a) a few thousand in number
(b) more than ten thousand in number
Ans: (a) Leaves of tree, grains of rice, seeds, dry fruits.
(b) Grains of sand, words in a book, strands of hair, threads in a fabric, pixels on a T.V screen.
Try to guess within 30 seconds. Check your guess with your friends.
Q1: Number of words in your maths textbook:
(a) More than 5000
(b) Less than 5000
Ans: (a)
Q2: Number of students in your school who travel to school by bus:
(a) More than 200
(b) Less than 200
Ans: (a)
Q3: Roshan wants to buy milk and 3 types of fruit to make fruit custard for 5 people. He estimates the cost to be 100. Do you agree with him? Why or why not?
Ans: Estimated cost of milk = 60
Estimated cost of 3 fruits = 150 (₹50 for each fruit)
Estimated cost of custard powder = 50
Total estimated cost of making custard = 60 + 50 + 150 = 260.
No, I don't agree withRoshan's estimate because I think cost of making custard for 5 people is likely to be around 260.
Q4: Estimate the distance between Gandhinagar (in Gujarat) to Kohima (in Nagaland). [Hint: Look at the map of India to locate these cities.]
Ans: 3000 km.
Page 71
Q5: Sheetal is in Grade 6 and says she has spent around 13,000 hours in school till date. Do you agree with her? Why or why not?
Ans: Total school days per year = 210
Total hours spent in school per day = 6 hours
Total hours spent in school per year = 210 × 6
= 1260 hours
Total number of years in school by Grade 6 = 8 years
Therefore, total hours spent in school in 8 years = 1260 x 8
= 10,080 hours.
No, I don't agree with Sheetal's estimate that she has spent around 13,000 hours in school till date because I think the more reasonable estimate would be around 10,000 hours.
Q6: Earlier, people used to walk long distances as they had no other means of transport. Suppose you walk at your normal pace. Approximately how long would it take you to go from:
(a) Your current location to one of your favourite places nearby.
(b) Your current location to any neighbouring state's capital city.
(c) The southernmost point in India to the northernmost point in India.
Ans: (a) Approximately 1 hour.
(b) Around 7-8 days.
(c) Around 100 days.
Q7: Make some estimation questions and challenge your classmates!
Ans: To be done by the students.
Page 72
Figure it Out
Q1: There is only one supercell (number greater than all its neighbours) in this grid. If you exchange two digits of one of the numbers, there will be 4 supercells. Figure out which digits to swap.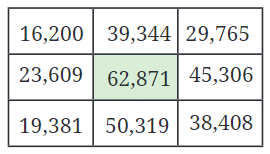 Ans: If you swap '6' of the supercell 62,871 with '1', then there will be 4 supercells.
Ans: If you swap '6' of the supercell 62,871 with '1', then there will be 4 supercells.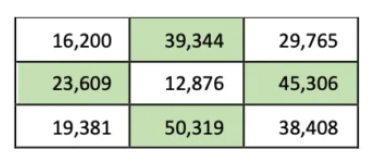
Q2: How many rounds does your year of birth take to reach the Kaprekar constant?
Ans: Year of birth: 2012
1st round
Largest number = 2210
Smallest Number = 0122
Subtract = 2210 - 0122
= 2088
2nd round
Largest number = 8820
Smallest number = 0288
Subtract = 8820 - 0288
3rd round
Largest number = 8532
Smallest number =2358
Subtract = 8532-2358 = 6174
Therefore, the number 2012 takes 3 rounds to reach 6174 which is the Kaprekar constant.
Q3: We are the group of 5-digit numbers between 35,000 and 75,000 such that all of our digits are odd. Who is the largest number in our group? Who is the smallest number in our group? Who among us is the closest to 50,000?
Ans: The odd numbers between 35000 and 75000 are
35001, 35003, 35005, ……..74999.
Therefore, largest number = 74999,
smallest number = 35001
and closest to 50000 = 49999 or 50001.
Q4: Estimate the number of holidays you get in a year including weekends, festivals and vacation. Then try to get an exact number and see how close your estimate is.
Ans: Estimated number of holidays in a year including weekends, festivals and vacations = 155 days
Number of weeks in a year = 52 weeks
Holidays on Sundays = 52 days
Holidays on Saturdays (2 holidays per month) = 24
Public holidays = 15 days
Summer vacations = 45 days
Winter vacations = 15 days
Actual number of holidays in a year = 52 + 24 + 15 + 45 + 15 = 151 days.
Q5: Estimate the number of liters a mug, a bucket and an overhead tank can hold.
Ans: Capacity of a mug = 0.3 liters
Capacity of a bucket = 20 liters
Capacity of an overhead tank = 2000 liters.
Q6: Write one 5-digit number and two 3-digit numbers such that their sum is 18,670.
Ans: 5-digit number = 16,945
3-digit number = 825
3-digit number = 900
Sum 16,945 + 825 +900 = 18,670.
Q7: Choose a number between 210 and 390. Create a number pattern similar to those shown in Section 3.9 that will sum up to this number.
Ans: Chosen number = 320
In case of 10: 4 × 8 × 10 = 320
In case of 20: 4 x 4 x 20 = 320
Page 73
Q8: Recall the sequence of Powers of 2 from Chapter 1, Table 1. Why is the Collatz conjecture correct for all the starting numbers in this sequence?
Ans: Power of 2 sequence: 1, 2, 4, 8, 16, 32, 64, ...
Power of 2 sequence contains all even numbers.
When dividing an even number by 2, we will get an even number but by repeatedly dividing an even number by 2, we will eventually reach 1.
This is why Collatz conjecture is correct for all the starting numbers in this sequence.
Example: 16 (power of 2)
16/2 = 8
8/2 = 4
4/2 = 2
2/2 = 1
Q9: Check if the Collatz Conjecture holds for the starting number 100.
Ans: Collatz conjecture: If the number is even, take half of it;if the number is odd, multiply it by 3 and add 1.
If you continue doing this you will always reach number 1, regardless of the number you start with.
100 (even) : 100/2 = 50
50 (even): 50/2 = 25
25 (odd): 25 x 3 + 1 = 76
76 (even): 76/2 = 38
38 (even): 38/2= 19
19 (odd): 19 x 3 + 1 = 58
58 (even): 58/2 = 29
29 (odd): 29 x 3 + 1 = 88
88 (even): 88/2 = 44
44 (even): 44/2 = 22
22 (even): 22/2 = 11
11 (odd): 11 x 3 + 1 = 34
34 (even): 34/2 = 17
17 (even): 17 x 3 + 1 = 52
52 (even): 52/2 = 26
26 (even): 26/2 = 13
13 (odd): 13 x 3 + 1 = 40
40 (even): 40/2 = 20
20 (even): 20/2= 10
10 (even): 10/2 = 5
5 (odd): 5 x 3 + 1 = 16
16 (even): 16/2 = 8
8 (even): 8/2 = 4
4 (even): 4/2 = 2
2 (even): 2/2 = 1
Q10: Starting with O, players alternate adding numbers between 1 and 3. The first person to 10. reach 22 wins. What is the winning strategy now?
Ans: (i) Start by adding 3 on your first turn to reach 3.
(ii) Then, always move in such a way that you leave the opponent on a multiple of 4.
(iii) Following this strategy will ensure that you reach 22 first, securing the win.Page 59
|
48 videos|334 docs|23 tests
|
FAQs on Number Play NCERT Solutions - Mathematics for Class 6
| 1. What are the basic concepts covered in NCERT Solutions for Number Play? |  |
| 2. How can I use NCERT Solutions for Number Play to improve my child's math skills? |  |
| 3. Are NCERT Solutions for Number Play suitable for all grades? |  |
| 4. How do the activities in NCERT Solutions for Number Play facilitate learning? |  |
| 5. Where can I find the NCERT Solutions for Number Play? |  |





















