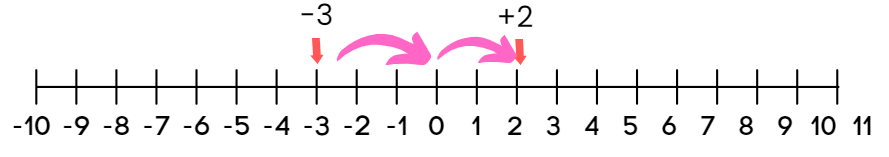Worksheet Solutions: The Other Side of Zero - 1

Multiple Choice Questions (MCQs)

Q1: What is the result of (-5) + (+3)?
(a) -8
(b) 2
(c) -2
(d) 8
Ans: (c) -2
Solution: Adding -5 and +3 results in -2 because you're moving 3 units to the right from -5.

Q2: Which of the following represents the correct inverse operation for subtracting -4?
(a) Adding +4
(b) Subtracting +4
(c) Adding -4
(d) None of the above
Ans: (a) Adding +4
Solution: Subtracting -4 is the same as adding +4.

Q3: What is the value of the expression (-6) - (-3)?
(a) -9
(b) -3
(c) -1
(d) -2
Ans: (b) -3
Solution: Subtracting -3 from -6 is the same as adding +3, which gives -3.

Q4: If you move 7 steps to the left from +2 on a number line, where will you end up?
(a) -5
(b) 5
(c) 9
(d) -9
Ans: (a) -5
Solution: Moving 7 steps left from +2 lands you at -5.

Q5: The sum of -7 and -3 is closest to which of the following?
(a) -10
(b) 10
(c) -4
(d) 4
Ans: (a) -10
Solution: Adding -7 and -3 results in -10.

Fill in the Blanks

Q1: The number line extends infinitely in both directions, with positive numbers on the right of 0 and _______ numbers on the left.
Ans: Negative
Solution: Negative numbers are those less than zero and are represented to the left of 0 on the number line.

Q2: The additive inverse of +7 is _______.
Ans: -7
Solution: The additive inverse of a number is what you add to it to get zero. For +7, the additive inverse is -7.

Q3: When you subtract a negative number, it is the same as _______ the corresponding positive number.
Ans: Adding
Solution: Subtracting a negative number is equivalent to adding the positive counterpart of that number.

Q4: On a number line, moving to the left signifies _______, while moving to the right signifies _______.
Ans: Subtraction, Addition
Solution: Moving left on the number line decreases the value (subtraction), while moving right increases it (addition).

Q5: The sum of a number and its inverse is always _______.
Ans: Zero
Solution: Adding a number to its additive inverse results in zero.

True/False

Q1: The number zero is considered neither positive nor negative.
Ans: True
Solution: Zero is neutral, lying between positive and negative numbers on the number line.

Q2: The number -5 is greater than the number -3.
Ans: False
Solution: On the number line, -5 is to the left of -3, making it smaller.

Q3: Subtracting a positive number is the same as adding its inverse.
Ans: True
Solution: Subtracting a positive number reduces the value, equivalent to adding its negative counterpart.

Q4: If you add two negative numbers, the result is always positive.
Ans: False
Solution: Adding two negative numbers gives a negative result.

Q5: On the number line, -1 is closer to zero than -2.
Ans: True
Solution: The number -1 is closer to zero on the number line than -2.

Practical Application Questions

Q1: Draw a number line and mark the points -3, 0, and +4. Indicate the position you will reach if you move 5 units to the right from -3.
Ans:

1. Step 1: First, let's draw a number line. A number line is like a ruler, but it can go into negative numbers too. Label the numbers from -5 on the left to +5 on the right.

2. Step 2: Mark the points -3, 0, and +4 on the number line. To do this:

   • Start at 0 in the middle.
   • Move 3 steps to the left of 0 to reach -3.
   • Stay at 0.
   • Move 4 steps to the right of 0 to reach +4.

3. Step 3: Now, if we start at -3 and move 5 steps to the right, let's see where we land:

   • Start at -3.
   • Move 1 step to the right to reach -2.
   • Move another step to reach -1.
   • Keep moving right to 0, +1, and finally +2.

The final position is +2.
Solution: When you move 5 steps to the right from -3, you pass through -2, -1, 0, +1, and land on +2. Moving right means you are adding, so -3 + 5 equals +2.

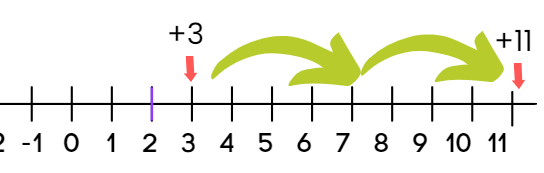
Q2: Subtract -8 from +3 using a number line. Show the process and the final result.
Ans:

1. Step 1: Start by drawing a number line and label it from -10 on the left to +10 on the right.

2. Step 2: Place yourself at +3 on the number line. Now, you need to subtract -8. Subtracting a negative number is like adding its positive counterpart. So instead of moving left, you move to the right.

3. Step 3: Starting at +3, move 8 steps to the right:

   • Move from +3 to +4, +5, +6, +7, +8, +9, +10, and finally +11.

The result is +11.
Solution: When you subtract -8 from +3, you're actually adding 8, because subtracting a negative is like adding the positive version. So +3 - (-8) = +3 + 8 = +11.

Word problems

Q1. A lift in a building starts at the 7th floor.

A) The lift moves down 5 floors. What floor does it reach?

B) From that floor, the lift moves up 3 floors. Where is the lift now?

C) Finally, the lift moves down 4 floors. What floor does it stop at?

Ans:

A) After moving down 5 floors:

7-5=2

The lift is on the 2nd floor.

B) After moving up 3 floors:

$2+3=52\; +\; 3\; =\; 5$

The lift is now on the 5th floor.

C) After moving down 4 floors:

$5-4=15\; -\; 4\; =\; 1$

The lift is on the 1st floor.

Q2. In a bank, the balance of an account is recorded.

A) John has a balance of ₹500 in his account. He withdraws ₹200. What is his new balance?

B) Then, he deposits ₹150 into his account. What is his balance now?

C) After that, he withdraws ₹100. What is his final balance?

Ans:

A) After withdrawing ₹200:

500-200=300

John's new balance is ₹300.

B) After depositing ₹150:

300+150=450

John's balance is now ₹450.

C) After withdrawing ₹100:

450-100=350

John's final balance is ₹350.

Q3. A miner is working in a mineshaft where the surface level is represented by 0 meters.

A. The miner starts at -10 meters below the surface and then descends 5 meters further. What is his new depth?

B. After that, the miner ascends 8 meters. What is his new depth now?

C. Finally, the miner descends 3 meters. Where is he now?

Ans:

​A. After descending 5 meters from -10 meters:

-10-5=-15

The miner is now at -15 meters.

B. After ascending 8 meters:

-15+8=-7

The miner is now at -7 meters.

C. After descending 3 meters:

-7-3 = -10

The miner is now at -10 meters.