Previous Year Questions: Number System | Digital Logic - Computer Science Engineering (CSE) PDF Download
Q1: Which of the following is/are EQUAL to 224 in radix-5 (i.e., base-5) notation? (2024 SET-2)
(a) 64 in radix-10
(b) 100 in radix-8
(c) 50 in radix-16
(d) 121 in radix-7
Ans: (a, b, d)
Sol:
To check the equivalent between numbers simply convert it into decimal format
(224)5 = 4 * 50 + 2 * 51 + 2 * 52 = (64)10
(100)8 = 0 * 80 + 0 * 81 + 1 * 82 = (64)10
(50)16 = 0 * 160 + 5 * 161 = (80)10
(121)7 = 1 * 70 + 2 * 71 + 1*72= (64)10
Option A, B, D is correct.
Q2: The format of a single-precision floating-point number as per the IEEE 754 standard is: 
Choose the largest floating-point number among the following options. (2024 SET-2)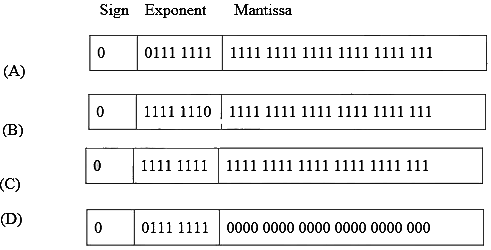
(a) A
(b) B
(c) C
(d) D
Ans: (b)
Sol:
Setting exponent as 11111110. Also mantissa will be all 1's. This combination will result in the largest FPN.
Note that here the LSB is not 1. Setting all exponent bits to 1 will result in a spcl notation which is reserved in IEEE 754 format.
Q3: Consider a system that uses 5 bits for representing signed integers in 2's complement format. In this system, two integers A and B are represented as A01010 and B = 11010. Which one of the following operations will result in either an arithmetic overflow or an arithmetic underflow? (2024 SET-1)
(a) A + B
(b) A - B
(c) B - A
(d) 2 * B
Ans: (b)
Sol:
As we know the range of 2's complement number is-2n-1 to (2n-1-1) because the given data is five-bit long so its range is -16 to +15.
First calculate the value of A, В.
- A=01010+10 as the MSB bit is zero so the number is positive.
- B=11010248-6 as MSB bit is one so the number is negative.
Option A) A + B = +10 + (-6) = +4
Option B) A - B = +10 - (-6) = +16. To represent (+16)10 = (010000)2 it required total of six bits
which is clearly out of range.
Option C) B - A = -6 - (+10) = -16
Option D) 2 * B = 2 * (-6) = -12
So Option (B) is correct.
Q4: Consider the IEEE-754 single precision floating point numbers P = 0xC1800000 and Q = 0x3F5C2EF4.
Which one of the following corresponds to the product of these numbers (i.e., P x Q), represented in the IEEE-754 single precision format? (2023)
(a) 0x404C2EF4
(b) 0x405C2EF4
(c) 0xC15C2EF4
(d) 0xC14C2EF4
Ans: (c)
Sol:
P = 0xC1800000 = 1100 0001 1000 0000 0000 0000 0000 0000 IEEE 754 Single Precision Format (32-bit)–
Biased Exponent = 131
Actual Exponent = Biased Exponent - Bias (28-1- 1) = 131 - 127 = 4
Mantissa = 0000 0000 0000 0000 0000 000
Actual Number = 1.00000000000000000000000 * 24 = 16 (It is negative 16 because sign bit is 1)
Q = 0x3F5C2EF4 = 0011 1111 0101 1100 0010 1110 1111 0100
Sign = 0 (Positive),
Biased Exponent = 01111110 = 126
Actual Exponent = 126-127 = 2-1
Mantissa = 10111000010 1110 1111 0100
P * Q = 1.0000 * 1.1011100 0010 1110 1111 0100 * 24 * 2-1 = 1.10111000010111011110100 * 23
Representing back to IEEE 754
Sign Bit = 1
Biased Exponent = 127 + 3 = 130 = 10000010
Mantissa: 1011 10000101 1101 1110 100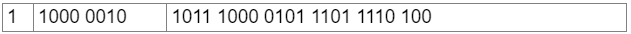
= 1100 0001 0101 11000010 1110 1111 0100 = C15C2EF4
Q5: A particular number is written as 132 in radix-4 representation. The same number in radix-5 representation is (2023)
(a) 158
(b) 118
(c) 110
(d) 98
Ans: (c)
Sol:
(132)4
= (1 * 42 + 3 * 41 + 2 * 40)10
= (30)10
= (25 + 5 + 0) 10 [powers of 5]
= (1 * 52 + 1 * 51 + 0 * 50) 10
= (110) 5
Answer is 110.
Q6: Consider three floating point numbers A, B and C stored in registers RA, RB and RC, respectively as per IEEE-754 single precision floating point format. The 32-bit content stored in these registers (in hexadecimal form) are as follows.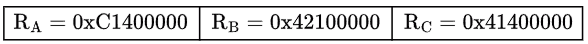
Which one of the following is FALSE? (2022)
(a) A + C = 0
(b) C = A + B
(c) B = 3C
(d) (B - C) > 0
Ans: (b)
Sol:
Given that Numbers are in IEEE-754 single precision.
Representation :: 1 sign bit, 8 exponent bits and 23 Mantissa Bits
Decimal value = (-1)Sign bit × (1.Mantissa) × (2) exponent-127
RA = 0xC1400000 = 1100 0001 0100 0000 0000 0000 0000 0000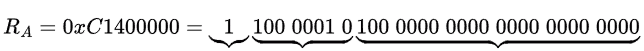
Decimal value of RA = (-1)1 × (1.1000000000..) × (2) 130-127 = (1100)2 = -12
RB = 0x42100000 = 0100 0010 0001 0000 0000 0000 0000 0000
Decimal value of RB = (-1)0 × (1.001000000000..) × (2) 132-127 = -(100100)2 = 3
RC = 0x41400000 = 0100 0001 0100 0000 0000 0000 0000 0000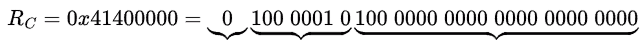
Decimal value of RC = (-1)0 × (1.1000000000..) × (2)130-127 = (1100)2 = 12
∴ C = A + B is false.
Alternate:
RA = 0xC1400000, RB = 0x42100000 and RC = 0x41400000
i. By observing RA and RC only MSB bit is different ===> RC = -RA ===> RC + RA = 0
ii. By observing RB and RC, RB exponent part is higher than RC exponent part ===>
RB > RC ===> RB - RC > 0
Now Verify other two options.
Q7: Let R1 and R2 be two 4-bit registers that store numbers in 2's complement form. For the operation R1+R2, which one of the following values of R1 and R2 gives an arithmetic overflow? (2022)
(a) R1 = 1011 and R2 = 1110
(b) R1 = 1100 and R2 = 1010
(c) R1 = 0011 and R2 = 0100
(d) R1 = 1001 and R2 = 1111
Ans: (b)
Sol:
Note: A simple range measurement would be sufficient to tell whether the addition of similarly signed two numbers causes an overflow. See the last paragraph for a much simpler explanation.
Theory(Stub),
Knowing weighted code representation for identifying 2's complement would help in identifying whether the number is positive or negative.
MSB=1 implies the number is negative and MSB=0 implies it's positive (considering 0 on the positive spectrum).
In 2's complement addition, an adder is used irrelevant of the sign of the two numbers, adding numbers with similar signs causes overflow, due to the inability to accommodate bits required to represent positive and negative parts of the number within fixed bit size. And, adding a
number with different signs doesn't cause overflow because they negate each other and therefore could be represented with the same or few number of bits.
Overflow for Positive Numbers,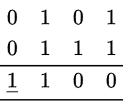
Here, the sign bit(MSB) is occupied by 1(a resultant from the positive component addition), there’s no other way to accommodate this number and maintaining 2’s complement nature without resorting to another bit.
Sign Bit Compaction for negative numbers,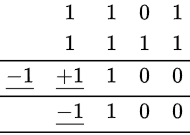
Here, we consider the addition of the Two MSB of a negative number leading to a larger negative component-2N but and there's a positive component 2N-1 addition of these two would result in -2N-1 which could be accommodated in the sign bit or simply omit the leftover carry.
Overflow for Negative Numbers,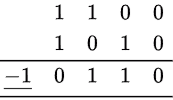
Unlike the previous example, there’s no way compacting the sign bit hence it, causes a overflow.
4bit 2's complement range: [-23, 23 - 1] = [-8, 7], convert the above options to decimal numbers and them to see whether they lie within the above range.
In Option B, we note that the addition of 1100(-4) and 1010(-6) results in -10 which is larger than what we could be able to accommodate in this range.
Or, the above case example concerning overflow for negative numbers.
Q8: If the numerical value of a 2-byte unsigned integer on a little endian computer is 255 more than that on a big endian computer, which of the following choices represent(s) the unsigned integer on a little endian computer? (2021 SET-2)
(a) 0x6665
(b) 0x0001
(c) 0x4243
(d) 0x0100
Ans: (a, d)
Sol:
concept:
If you split hex number into bytes,
In hexadecimal representation, each digit corresponds to 4 binary digits.(i.e 2 hex digits = 8 bits= 1 byte).
If little-endian representation used then byte arrangement is as follows:
If little-endian representation used then byte arrangement is as follows:
if Big endian representation is used then the byte arrangement is as follows:
Within the byte no change in the bit sequence.
A) 0x0001 is incorrect.
Little-endian 0x0001 gives you 01 as the first byte and 00 as the second byte, o the corresponding big-endian representation is 0x0100.
Hex (0x0001) is equal to 1 in decimal
Hex(0x0100) is equal to 256 in decimal.
Their difference is -255.
B) 0x6665 is correct
Little-endian 0x6665 gives you 65 as the first byte and 66 as the second
byte, So the corresponding big-endian representation is 0x6566.Hex (0x6665) is equal to 26213 in decimal
Hex(0x6566) is equal to 25958 in decimal.
Their difference is 255.
C) 0x0100 is correct
Little-endian 0x0100 gives you 00 as the first byte and 01 as the second
byte, So the corresponding big-endian representation is 0x0100
Hex(0x0100) is equal to 256 in decimal.,
Hex (0x0001) is equal to 1 in decimal
Their difference is 255.
D) 0x4243 is incorrect
Little-endian 0x4243 gives you 43 as first byte and 42 as the second byte, So
the corresponding big-endian representation is 0x4342
Hex(0x4243) is equal to 16963 in decimal.
Hex (0x4342) is equal to 17218 in decimal.
Their difference is -255.
So 2,3 is the answer
Q9: If x and y are two decimal digits and (0.1101)2 = (0.8xy5) 10, the decimal value of x + y is (2021 SET-2)
(a) 3
(b) 6
(c) 8
(d) 4
Ans: (a)
Sol:
(0.1101)2 = (0.8xy5) 10
After decimal point 4 digits present apply left shit 4 times.
∴ If base is 2, shift 4 numbers to left side and multiply with 2-4.
If base is 10, shift 4 numbers to left side and multiply with 10-4.
(1101) × 2-4 = (8xy5) * 10-4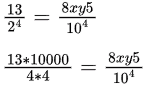
8125 = 8xy5 ⇒ x = 1, y = 2.
∴ x + y = 3
Q10: The format of the single-precision floating point representation of a real number as per the IEEE 754 standard is as follows:
Which one of the following choices is correct with respect to the smallest normalized positive number represented using the standard? (2021 SET-2)
(a) exponent = 00000000 and mantissa = 0000000000000000000000000
(b) exponent = 00000000 and mantissa = 0000000000000000000000001
(c) exponent = 00000001 and mantissa = 0000000000000000000000000
(d) exponent = 00000001 and mantissa = 0000000000000000000000001
Ans: (c)
Sol:
Concept:
In IEEE-754 single precision format, a floating-point number is represented in 32 bits.
Sign bit value 0 means a positive number, and 1 means a negative number.
The floating-point number can be obtained by formula: (-1)s x 1.M x 2E-127
Explanation:
Smallest normalized positive number
Smallest normalized positive = (-1)0 x 1.00...0 x 21-127 = 2-126 ≈ 1.1755 × 10-38
Q11: Consider the following representation of a number in IEEE 754 single-precision floating point format with a bias of127.
S:1
E:10000001
Here, S,E and F denote the sign, exponent, and fraction components of the floating point representation. (2021 SET-1)
The decimal value corresponding to the above representation (rounded to 2 decimal places) is ____
(a) -7.75
(b) 7.75
(c) -3.825
(d) 3.825
Ans: (a)
Sol:
-7.75 is the correct answer.
Here, Sign bit = 1 number is negative.
Exponent bits = 10000001 = 12910 → E = 129 - 127 = 2 as IEEE-754 single precision format uses 127 as the exponent bias.
Mantissa bits = 11110000000000000000000
Number = -1.111100...00 × 22 = (-111.11)2
∴ Number = (-7.75)10.
Q12: Let the representation of a number in base 3 be 210. What is the hexadecimal representation of the number? (2021 SET-1)
(a) 15
(b) 21
(c) D2
(d) 528
Ans: (a)
Sol:
Firstly convert base 3 into a decimal number system(Base 10):
(210)3 = (x)10 ⇒ 0 * 30+ 1 * 31+ 2 * 32 = (21)10
Now convert (21)10 into a hexadecimal system. dividing by 16 that is:
(21)10 = (2)16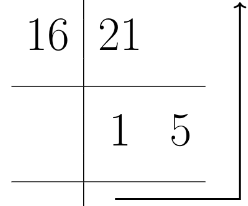
z = (15) 16
Option A is correct.
Q13: Consider three registers R1, R2, and R3 that store numbers in IEEE-754 single precision floating point format. Assume that R1 and R2 contain the values (in hexadecimal notation) 0x42200000 and 0xC1200000, respectively.
If R3 = R1/R2 what is the value stored in R3? (2020)
(a) 0x40800000
(b) 0xC0800000
(c) 0x83400000
(d) 0xC8500000
Ans: (b)
Sol:
Concept:
In IEEE- 754 single precision format, a floating-point number is represented in 32 bits.
Sign bit value 0 means positive number, and 1 means a negative number.
The floating-point number can be obtained by formula: ± 1. M x 2(E-127)
Data:
Content of R1: 0x 42200000 (Ox means Hexadecimal notation)
Content of R2: 0x C120000
Calculation:
Content of R1 in Hex (0x) is 42200000. After converting into binary, it can be represented in IEEE-754 format as:
Sign bit is 0 i.e. the number is positive
Biased Exponent (E') = 100 0010 0 = 132
Normalized Mantissa (M) = 010 0000 0000 0000 0000 0000 = .25
Therefore, the number in register R1 = + 1.25 * 2(132-127) = 1.25 x 32 = 40
Content of R2 in Hex (0x) is C1200000. After converting into binary, it can be represented in IEEE- 754 format as:
Sign bit is 1 i.e. the number is negative
Biased Exponent (E') = 100 0001 0 = 130
Normalized Mantissa (M) = 010 0000 0000 0000 0000 0000 = .25
Therefore, the number in register R1 = - 1.25 * 2(130-127) = -1.25 * 8 = -10
R3 = R1/R2 = 40/-10 = -4
Since the number is negative, Sign bit (MSB) = 1
Converting 4 into binary of a floating point gives: (100.0)2
Representing it into normalized form gives: (1.000000....) x 22
Therefore, Mantissa is 23 bits of all 0s
Biased Exponent (E') = E+ 127 = 2+ 127 = 129 = (10000001)2
It can be represented in IEEE- 754 format as: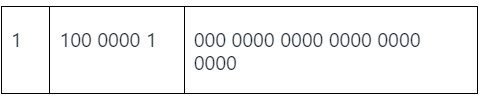
Converting it into Hex format gives: 0x C0800000
Q14: Consider Z = X - Y where X, Y and Z are all in sign-magnitude form. X and Y are each represented in n bits. To avoid overflow, the representation of Z would require a minimum of: (2019)
(a) n bits
(b) n - 1 bits
(c) n + 1 bits
(d) n + 2 bits
Ans: (c)
Sol:
Let X and Y represents 31 and -31 respectively in binary sign magnitude form. X and Y will take 6 bit as range of sign magnitude form is
(2(n-1) - 1) to 2(n-1) - 1; where n is the number of bits.
Now in question Z = X - Y,
Z = 31 - (-31) = 62
To represent 62 in sign magnitude form we need 7 (6+1) bits.
Hence, n + 1 bits needed.
Answer is C.
Q15: In 16-bit 2's complement representation, the decimal number -28 is: (2019)
(a) 1111 1111 0001 1100
(b) 0000 0000 1110 0100
(c) 1111 1111 1110 0100
(d) 1000 0000 1110 0100
Ans: (c)
Sol:
(+28)10 (0000 0000 00011100)2
-28 is nothing but 2s complement of +28.
So, 2s complement of (0000 0000 0001 1100)2 is (1111 1111 1110 0100)2
(-28)10 (1111 1111 1110 0100)2.
Answer is (C).
Q16: Consider the unsigned 8-bit fixed point binary Number System below,
b7b6b5b4b3 .b2b1b0
where the position of the binary point is between b3 and b2. Assume b7 is the most significant bit. Some of the decimal numbers listed below cannot be represented exactly in the above representation: (2018)
(i) 31.500 (ii) 0.875 (iii) 12.100 (iv) 3.001
Which one of the following statements is true?
(a) None of (i), (ii), (iii), (iv) can be exactly represented
(b) Only (ii) cannot be exactly represented
(c) Only (iii) and (iv) cannot be exactly represented
(d) Only (i) and (ii) cannot be exactly represented
Ans: (c)
Sol:
31.500 can be represented as 11111.100 in the above mentioned fixed form representation
0.875 can be represented as 00000.111.
We can't represent 3 and 4.
Hence, C is the correct answer.
Q17: Given the following binary number in 32-bit (single precision) IEEE-754 format: (2017 SET-2)
00111110011011010000000000000000
The decimal value closest to this floating-point number is
(a) 1.45 * 101
(b) 1.45 * 10-1
(c) 2.27 * 10-1
(d) 2.27 * 101
Ans: (c)
Sol:
In 32 bit (single precision) IEEE-754 format, binary number is represented as
S(1 bit) E(8 bit) M(23 bits) with implicit normalization and exponent is represented with Excess-127 code.
Here, Sign bit = 0 → Number is positive.
Exponent bits = 01111100 = 124 ⇒ E124 - 127 = -3 (Excess-127)
Mantissa bits = 1101101000000000000000 ⇒ Number = 1.1101101 (Implicit normalization).
∴ Number = 1.1101101 * 2-3 = 0.0011101101 = 0.2272.27 × 10-1
The answer should be C.
Q18: The representation of the value of a 16-bit unsigned integer X in hexadecimal number system is BCA9. The representation of the value of X in octal number system is (2017 SET-2)
(a) 571244
(b) 736251
(c) 571247
(d) 136251
Ans: (d)
Sol:
Given: (BCA9)16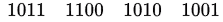
For octal number system: grouping of three-three bits from right to left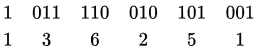
Answer: option D) (136251)8
Q19: The n-bit fixed-point representation of an unsigned real number real X uses f bits for the fraction part. Let i = n - f. The range of decimal values for X in this representation is (2017 SET-1)
(a) 2-f to 2i
(b) 2-f to (2i - 2-f)
(c) 0 to 2i
(d) 0 to (2i - 2-f)
Ans: (d)
Sol:
Unsigned real number x.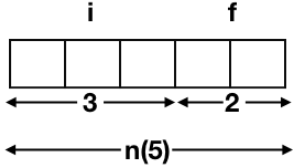
Let n = 5, f = 2, i = 5 - 2 = 3.
1. Minimum value of x: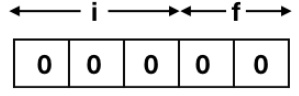
Value on decimal = 0.
2. Maximum value of x:
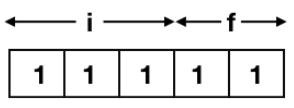
Value on decimal = 232-28-0.25 7.75 (Or 22 + 21 + 20 + 2-1 + 2-2 = 7.75)
So (D) is the answer.
Q20: Let X be the number of distinct 16-bit integers in 2's complement representation. Let Y be the number of distinct 16 bit integers in sign magnitude representation. Then X-Y is (2016 SET-2)
(a) 0
(b) 1
(c) 2
(d) 16
Ans: (b)
Sol:
2's Complement Representation
The range of n-bit 2's Complement Numbers is -(2n-1) to +(2n-1 - 1)
For example, if n = 2, then -2, -1, 0, 1 belong to the range(which are distinct)
In general 2n distinct integers are possible with n-bit 2's Complement Number → X
Sign Magnitude Representation
The range of n-bit Sign Magnitude numbers is -(2n-1 - 1) to +(2n-1 - 1)
For example, if n = 2, then 1, 0, +0, +1 belong to the range in which -0 = +0 and both
represent zero.
In general 2n - 1 distinct integers are possible with n-bit Sign magnitude representation → Y
X - Y = 2n - (2n -1) = 1.
Q21: The 16 bit 2's complement representation of an integer is 1111 1111 1111 0101: its decimal representation is ______. (2016 SET-1)
(a) -11
(b) 11
(c) 10
(d) -10
Ans: (a)
Sol:
1111 1111 1111 0101
2's complement of 1111 1111 1111 0101 = 0000 0000 0000 1011 = +11
2's complement of -11 = +11, in 2's complement representation
2's complement of +11 = -11, in 2's complement representation
So -11 it should be.
Q22: Consider the equation (43)x (y3)8 where x and y are unknown. The number of possible solutions is ______ (2015 SET-3)
(a) 2
(b) 4
(c) 5
(d) 7
Ans: (c)
Sol:
Digit constraints: In any base-k number system, digits can only range from 0 to k-1. In base 8, this means digits can be from 0 to 7. Therefore, x must be greater than 5 and y must be less than 7.
Expanding the equation: We can convert the equation to decimal form:
(43)x = 4 * x1 + 3 * x0 = 4x + 3
(y3)8 = y * 81 + 3 * 80 = 8y + 3
Simplifying and solving: Combining the expressions and solving for x, we get:
4x + 3 = 8y + 3
8y = 4x
x = 2y
Finding possible solutions: Now, we substitute values for y within the constraints mentioned in step 1:
y = 3 => x = 6
y = 4 => x = 8
y = 5 => x = 10
y = 6 => x = 12
y = 7 => x = 14
Therefore, there are 5 possible solutions for the equation: (x, y) = (6, 3), (8, 4), (10, 5), (12, 6). (14, 7).
So possible number of solution is 5.
Q23: The value of a float type variable is represented using the single-precision 32-bit floating point format of IEEE-754 standard that uses 1 bit for sign, 8 bits for biased exponent and 23 bits for mantissa. A float type variable x is assigned the decimal value of -14.25. The representation of x in hexadecimal notation is (2014 SET-2)
(a) C1640000H
(b) 416C0000H
(c) 41640000H
(d) C16C0000H
Ans: (a)
Sol:
Concept:
32-bit floating-point representation of a binary number in IEEE- 754 is
In IEEE-754 format, 32-bit (single precision)
(-1)s x 1.M x 2E-127
Calculation:
Convert: 14.25 to binary
Step 1: convert 40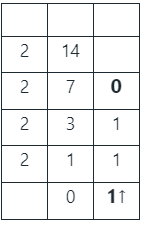
(14)2 = (1110)2
Step 2: convert.25 to binary
0.25 x 2 = 0.5 (0)
0.5 x 2 = 1.0 (1)
Given binary number is
(40.1)10 = (1110.01)2
(40.1)10 = 1.11001 x 23
Signed (1 bit) = 1 (given number is negative)
Exponent (8 bit) = 3 + 127 = 130
Exponent = (130)10 = (10000010)2
Mantissa (23 bits) = 0100 0000 1100 1100 1100 110
(1100 0001 0110 0100 0000 0000 0000 0000)2 = (C1640000)16
(C2206666)16 = C1640000H
Q24: Consider the equation (123)5 = (x8)y with x and y as unknown. The number of possible solutions is (2014 SET-2)
(a) 2
(b) 3
(c) 4
(d) 5
Ans: (b)
Sol:
Converting both sides to decimal,
25 + 10 + 3 = x * y + 8
So, xy = 30
Possible pairs are (1, 30), (2, 15), (3, 10) as the minimum base should be greater than 8.
Q25: The base (or radix) of the number system such that the following equation holds is_______. (2014 SET-1)
312/20 = 13.1
(a) 4
(b) 5
(c) 6
(d) 7
Ans: (b)
Sol:
Let ‘x’ be the base or radix of the number system.
The equation is :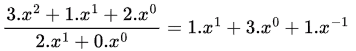
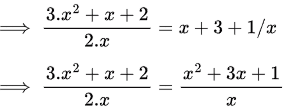
⇒ 3.x2 + x + 2 = 2.x2 + 6x + 2
⇒ x2 + -5x = 0
⇒ x(x - 5) = 0
⇒ x = 0 or x = 5
As base or radix of a number system cannot be zero, here x = 5.
Q26: The smallest integer that can be represented by an 8-bit number in 2's complement form is (2013)
(a) -256
(b) -128
(c) -127
(d) 0
Ans: (b)
Sol: Range of 2's compliment no ⇒ (-2n-1) to +(2n-1 -1)
Here n = No of bits = 8.
So minimum no = -27 = -128
Q27: The decimal value 0.5 in IEEE single precision floating point representation has (2012)
(a) fraction bits of 00 . . . 000 and exponent value of 0
(b) fraction bits of 000 . . . 000 and exponent value of -1
(c) fraction bits of 100 . . . 000 and exponent value of 0
(d) no exact representation
Ans: (b)
Sol:
(B) is the answer. IEEE 754 representation uses normalized representation except when all the exponent bits are zeroes (these are used for representing denormalized numbers and ±0) or when all the exponent bits are 1's (these are for representing ±0∞ and NaNs). So, here an implicit '1' is used before the decimal point.
So, if mantissa is:
0000 . . . 0
It would be treated as:
1.000 . . . 0
and hence, the exponent need to be -1 for us to get 0.1 which is the binary representation of 0.5.
Q28: P is a 16-bit signed integer. The 2's complement representation of P is (F87B) 16.
The 2's complement representation of 8 * P is (2010)
(a) (C3D8)16
(b) (187B)16
(c) (F878)16
(d) (987B)16
Ans: (a)
Sol:
Multiplication can be directly carried in 2's complement form.
F87B = 1111100001111011 can be left shifted 3 times to give 8P = 1100001111011000 = C3D8.
Or, we can do as follows:
MSB in (F87B) is 1. So, P is a negative number. So, P = -1 * 2's complement of
(F87B)= -1* (0785) = -1* (0000011110000101)
8 * P = -1* (0011110000101000) (P in binary left shifted 3 times)
In 2's complement representation, this equals, 1100001111011000 = C3D8
Correct Answer: A
|
53 docs|15 tests
|
FAQs on Previous Year Questions: Number System - Digital Logic - Computer Science Engineering (CSE)
| 1. What is a number system in computer science? |  |
| 2. Why is binary the primary number system used in computers? |  |
| 3. How do you convert numbers between different number systems? |  |
| 4. What is the significance of hexadecimal in computer science? |  |
| 5. How do number systems impact computer arithmetic operations? |  |





















