Previous Year Questions: Memory Chip Design | Computer Architecture & Organisation (CAO) - Computer Science Engineering (CSE) PDF Download

Q1: A 4 kilobyte (KB) byte-addressable memory is realized using four 1 KB memory blocks. Two input address lines (IA4 and IA3) are connected to the chip select (CS) port of these memory blocks through a decoder as shown in the figure. The remaining ten input address lines from IA11-IA0 are connected to the address port of these blocks. The chip select (CS) is active high.
The input memory addresses (IA11-IA0), in decimal, for the starting locations (Addr=0) of each block (indicated as X1, X2, X3, X4 in the figure) are among the options given below. Which one of the following options is CORRECT?  (2023)
(a) (0, 1, 2, 3)
(b) (0, 1024, 2048, 3072)
(c) (0, 8, 16, 24)
(d) (0, 0, 0, 0)
Ans: (c)
Sol: A 4 KB memory is given.
4 KB = 2¹², means we require 12 bits for its representation. But, 4 KB memory is implemented as four 1 KB memory blocks.
Out of these 12 bits, 2 bits(I4 & I3) are connected to 2 : 4 Decoder.
4 output pins of decoder Q0, Q1, Q2, Q3 is connected to 4 chip select ports of X1, X2, X3 & X4 respectively.
With 2-bits we can generate 4 different configurations, which are sufficient to uniquely identify the memory block.
Q0, Q1, Q2, Q3 can be recognized by these corresponding values of I4 & I3 :
Remaining 10 bits are connected to address port of these blocks.
For starting location (Addr =0) we have to put all the bits from I0 – I11 as 0.
As the input memory address is in decimal.
So, Starting location (Addr = 0) for (X1, X2, X3, X4) are (0,8,16,24).
So, correct answer is C.

Q2: The chip select logic for a certain DRAM chip in a memory system design is shown below. Assume that the memory system has 16 address lines denoted by A₁₅ to A₀. What is the range of address (in hexadecimal) of the memory system that can get enabled by the chip select (CS) signal?  (2019)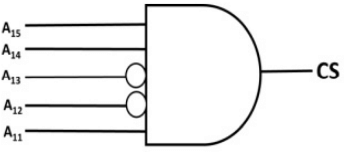
(a) C800 to CFFF
(b) CA00 to CAFF
(c) C800 to C8FF
(d) DA00 to DFFF
Ans: (a)
Sol: (A₁₅ A₁₄ A₁₃ A₁₂ A₁₁ A₁₀ A₉ A₈ A₇ A₆ A₅ A₄ A₃ A₂ A₁ A₀)
According to question:
A₁₅ = 1, A₁₄ = 1, A₁₃ = 0, A₁₂ = 0, A₁₁ = 1
So the possible range in binary:
(1100100000000000) to (1100111111111111)
Converting to Hexadecimal:
(C800) to (CFFF)
Option A.

Q3: A 32-bit wide main memory unit with a capacity of 1 GB is built using 256M x 4-bit DRAM chips. The number of rows of memory cells in the DRAM chip is 2¹⁴. The time taken to perform one refresh operation is 50 nanoseconds. The refresh period is 2 milliseconds. The percentage (rounded to the closest integer) of the time available for performing the memory read/write operations in the main memory unit is __________.  (2018)
(a) 60
(b) 65
(c) 55
(d) 70
Ans: (a)
Sol: One refresh operation takes 50ns.
Total number of rows = 2¹⁴
Total time to refresh all Rows = 2¹⁴ × 50ns = 819200ns = 0.819200ms
The Refresh Period is 2ms.
% Time spent in refresh  = (Total time to Refresh all Rows/Refresh period)∗100
= (0.8192ms/2.0ms) ∗ 100 = 40.96%
Time spent in Read/Write = 100 − 40.96 = 59.04%
= 59% (Rounded to the closest Integer)

Q4: How many 128x8 bit RAMs are required to design 32Kx32 bit RAM?  (2017)
(a) 512
(b) 1024
(c) 128
(d) 32
Ans: (b)
Sol: Number of RAM = (32 * K * 32) / 128 * 8
= 2⁵ * 2¹⁰ * 2⁵  /  2⁷ * 2³
= 2²⁰ / 2¹⁰
= 1024
option B...

Q5: How many 32K x 1 RAM chips are needed to provide a memory capacity of 256K-bytes?  (2015)
(a) 8
(b) 32
(c) 64
(d) 128
Ans: (c)
Sol: Total number of RAM chips

Q6: Suppose you want to build a memory with 4 byte words and a capacity of 2²¹ bits. What is type of decoder required if the memory is built using 2K × 8 RAM chips?  (2014)
(a) 5 to 32
(b) 6 to 64
(c) 4 to 16
(d) 7 to 128
Ans: (a)
Sol: Capacity of memory = 2²¹ bit
So, Capacity of memory in Byte will be = 2²¹/2³ = 2¹⁸ bytes
Word size of 4 Byte is given, from this we can calculate no. of words in memory = 2¹⁸/ 2² = 2¹⁶ words.
RAM chip size capacity is = 2K X 8 (means 8 bit word can be store in one cell of RAM), therefore, RAM capacity = 2¹¹ words.
No. of decoder line req. = 2¹⁶/2¹¹ = 2⁵ = 32

Q7: If each address space represents one byte of storage space, how many address lines are needed to access RAM chips arranged in a 4×6 array, where each chip is 8K × 4 bits ?   (2014)
(a) 13
(b) 15
(c) 16
(d) 17
Ans: (d)
Sol: see in the array there are 6 * 4  = 24 chip so to address them we need 5 bit .
and this is bye addressable "each address space represents one byte of storage space" .
so , for each chip 8k*4 bit = (2¹³⁺²)/8 Byte = 2¹² 
so for addressing we need (12 + 5 ) = 17 bits line

Q8: A RAM chip has a capacity of 1024 words of 8 bits each (1K x 8). The number of 2 x 4 decoders with enable line needed to construct a 16K x 16 RAM from 1K x 8 RAM is  (2013)
(a) 4
(b) 5
(c) 6
(d) 7
Ans: (b)
Sol: Actually we need decoders for selection of a row from address lines not data lines.
So you have to concentrate upon the first term of each of RAM size and chip size which are 16 K and 1 K respectively.
So no of address lines  =  16K / 1K = 16
Hence we can use 4 : 16 decoder for this .But we have to realise this using 2 : 4 decoder.
So this question now becomes actually of realisation of 4 : 16 decoder using 2 : 4 decoders.
So 4 decoders are required in inner level as from 1 2:4 decoder we have only 4 output lines whereas we need 16 output lines.
Now to point to these 4 decoders , another 2 : 4 decoder is required in the outer level .
Hence no of 2 : 4 decoders to realise the above implementation of RAM  = 1 + 4  =  5
Hence (B) is the correct answer.

Q9: The amount of ROM needed to implement a 4 bit multiplier is  (2012)
(a) 64 bits
(b) 128 bits
(c) 1 Kbits
(d) 2 Kbits
Ans: (d)
Sol: A ROM cannot be written. So, to implement a 4-bit multiplier we must store all the possible combinations of 2⁴ × 2⁴ inputs and their corresponding 8 output bits giving a total of 2⁴ × 2⁴ × 8 bits  = 2048 bits. So, (D) is the answer.
PS: We are not storing the input bits explicitly - those are considered in order while accessing the output 8 bits. In this way, by storing all the possible outputs in order we can avoid storing the input combinations.

Q10: Number of chips (128 × 8 RAM) needed to provide a memory capacity of 2048 bytes  (2011)
(a) 2
(b) 4
(c) 8
(d) 16
Ans: (d)
Sol: we have provided with chip if size, 128 x 8 = 128 Byte
and we need to create memory of 2048 Bytes
so we need to use 2048 / 128 = 16 chips lined one below another, i.e 16 rows
option D would be the answer,
lets assume we need to create memory of 2048 x 16 bit
then number of chips would have been 32
there would have been 16rows and each row with 2 chips

Q11: A main memory unit with a capacity of 4 megabytes is built using 1Mx1-bit DRAM chips. Each DRAM chip has 1K rows of cells with 1K cells in each row. The time taken for a single refresh operation is 100 nanoseconds. The time required to perform one refresh operation on all the cells in the memory unit is  (2010)
(a) 100 nanoseconds
(b) 100 *2¹⁰ nanoseconds
(c) 100*2²⁰ nanoseconds
(d) 3200*2²⁰ nanoseconds
Ans: (b)
Sol: There are 4∗8 = 32 DRAM chips to get 4MB from 1M × 1-bit chips. Now, all chips can be refreshed in parallel so do all cells in a row. So, the total time for refresh will be number of rows times the refresh time
= 1K × 100
= 100 × 2¹⁰ nanoseconds