Previous Year Questions: Calculus | Engineering Mathematics for Computer Science Engineering - Computer Science Engineering (CSE) PDF Download
Q1: Let f(x) be a continuous function from 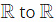 such that f(x) = 1 − f(2 − x).
such that f(x) = 1 − f(2 − x).
Which one of the following options is the CORRECT value of 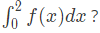 (2024 SET-2)
(2024 SET-2)
(a) 0
(b) 1
(c) 2
(d) -1
Ans: (b)
Sol: Given: f(x) = 1 − f(2 − x) → (1)
To find: 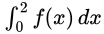
Method 1:
Notice that the continuous function f(x) = 1/2 from 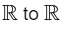 satisfies eqn. (1)
satisfies eqn. (1)
So, let f(x) = 1/2.
Now,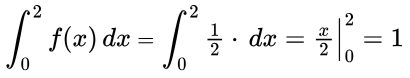 ∴ Ans = B.
∴ Ans = B.
A more formal method:
Let u = a − x, we have du = −dx, then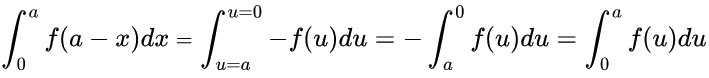 So,
So,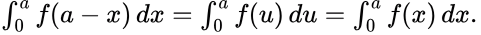 (∵ variable of integration is a dummy variable)
(∵ variable of integration is a dummy variable)
Now,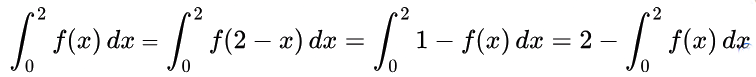
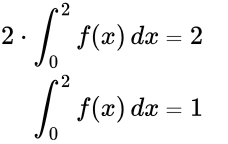
Q2: The value of the definite integral 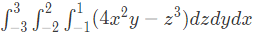 is _____. (Rounded off to the nearest integer) (2023)
is _____. (Rounded off to the nearest integer) (2023)
(a) 0
(b) 1
(c) 2
(d) 3
Ans: (a)
Sol: 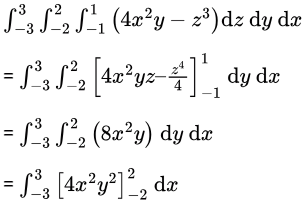
= 0
Answer is 0.
Q3: Let f(x) = x3 + 15x2− 33x − 36 be a real-valued function.
Which of the following statements is/are TRUE? (2023)
(a) f(x) does not have a local maximum.
(b) f(x) has a local maximum.
(c) f(x) does not have a local minimum.
(d) f(x) has a local minimum.
Ans: (b, d)
Sol: the real valued function f(x) = x3 + 15x2 − 33x − 36 = 0
(1) find f′(x) = 0
⇒ 3x2 + 30x − 33 = 0
⇒ x2 + 10x − 11 = 0
⇒ x2 + 11x − x − 11 = 0
⇒ (x + 11)(x − 1) = 0
⇒ x = −11, 1
(2) find f”(x) we get : f”(x) = 6x + 30
(3) f”(1) = 6 + 30 = 36 > 0 it is gives local minima
(4) f”(−11) = −66 + 30 = −36 < 0 it is gives local maxima.
so given function f(x) will give local maxima at x = −11 and local minima at x = 1
∴ Option B, D is correct.
Q4: The value of the following limit is _____ 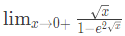 (2022)
(2022)
(a) -0.5
(b) 0.5
(c) 0
(d) 1
Ans: (a)
Sol: Given,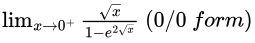 Using L'hopital rule
Using L'hopital rule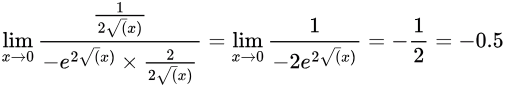
Q5: For two n-dimensional real vectors P and Q, the operation s(P, Q) is defined as follows: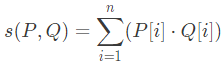 Let L be a set of 10-dimensional non-zero real vectors such that for every pair of distinct vectors P, Q ∈ L, s(P, Q) = 0. What is the maximum cardinality possible for the set L? (2021 SET-2)
Let L be a set of 10-dimensional non-zero real vectors such that for every pair of distinct vectors P, Q ∈ L, s(P, Q) = 0. What is the maximum cardinality possible for the set L? (2021 SET-2)
(a) 9
(b) 10
(c) 11
(d) 100
Ans: (b)
Sol: S(P, Q) is nothing but the dot product of two vectors.
The dot product of two vectors is zero when they are perpendicular, as we are dealing with 10 dimensional vectors the maximum number of mutually-perpendicular vectors can be 10.
So option B.
Q6: Suppose that f: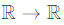 is a continuous function on the interval [-3, 3] and a differentiable function in the interval (-3, 3) such that for every xx in the interval, f′(x) ≤ 2. If f(−3) =7, then f(3) is at most _____ (2021 SET-2)
is a continuous function on the interval [-3, 3] and a differentiable function in the interval (-3, 3) such that for every xx in the interval, f′(x) ≤ 2. If f(−3) =7, then f(3) is at most _____ (2021 SET-2)
(a) 19
(b) 32
(c) 11
(d) 54
Ans: (a)
Sol: Given that f′(X) ≤ 2 and f(−3) = 7,
As maximum slope is positive and we need value of f(x) at 3 which is on right side of −3, we can assume f(x) as a straight line with slope 2. It will give us the correct result.
Let f(x) = 2x+b,
f(−3) = −6+b = 7 ⇒ b = 13
f(x) = 2x + 13
f(3)max = 6+13 = 19.
Correct method would be using Mean Value Theorem. Above method will work only if you can analyze the cases correctly and can assume the f(x) without any loss of accuracy, otherwise you are very prone to commit a mistake that way.
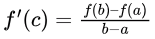
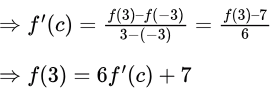 As f′(c) ≤ 2,
As f′(c) ≤ 2,⇒ f(3) ≤ 6 * 2 + 7 = 19.
Q7: Consider the following expression.
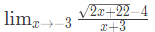 The value of the above expression (rounded to 2 decimal places) is ___________. (2021 SET-1)
The value of the above expression (rounded to 2 decimal places) is ___________. (2021 SET-1)(a) 0.25
(b) 0.45
(c) 0.75
(d) 0.85
Ans: (a)
Sol:
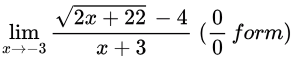 Using L'Hopital's rule
Using L'Hopital's rule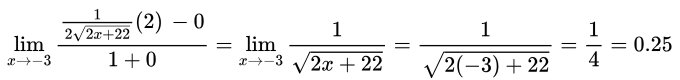
Q8: Consider the functions
I. e−x
II. x2 − sinx
III.
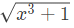
Which of the above functions is/are increasing everywhere in [0, 1] ?
(a) III only
(b) II only
(c) II and III only
(d) I and III only
Ans: (a)
Sol: Decreasing/Increasing nature of a function can be determined by observing the first derivative of equations in given domain.
If the derivative is positive in given domain, It is increasing, else a negative value indicates it is decreasing.
Now testing one by one
I. e−x
Here, (d/dx)e-x = -e-x
This will remain negative in entire domain [0, 1] hence decreasing.
II. x2 - sin(x)
Here,
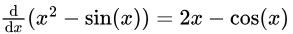
Here the switch happens! Observe 2x − cos(x) is negative for x = 0 (i.e. = -1) and positive at x = 1 (i.e. = ~1.4596977). Though we can find the exact point where it switches but that's not required here. We can confirm that till some point in the domain [0, 1], this function decreases and then increases.
iii.
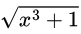
Here, (Though this one is intuitive),
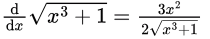 This will remain positive throughout [0, 1] and hence will be increasing.
This will remain positive throughout [0, 1] and hence will be increasing.Q9: Compute
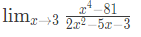 (2019)
(2019)(a) 1
(b) 53/12
(c) 108/7
(d) Limit does not exist
Ans: (c)
Sol: Let
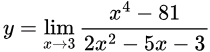
When we put 3 in the equation we get 0/0 form, so we can apply L Hospital′s rule.
Differentiate the numerator and denominator separately
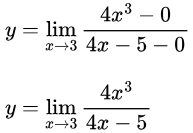 Put the limit and get the value
Put the limit and get the value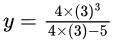
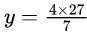 y = 108/7
y = 108/7Correct Answer is C.
Q10: The domain of the function log(log sin(x)) is: (2018)
(a) 0 < x < π
(b) 2nπ < x < (2n+1)π, for n in N
(c) Empty set
(d) None of the above
Ans: (c)
Sol: log( log sin(x) )
-1 <= sinx <= +1
log a is defined for positive values of a,
log sin(x) is defined for sin(x) = (0, 1]
Possible values for log sin(x) = (−∞, 0]
Domain of log( log sin(x) ) = Not defined
Therefore, Answer (c) Empty Set.
Q11: The value of
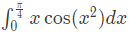 correct to three decimal places (assuming that π = 3.14 ) is (2018)
correct to three decimal places (assuming that π = 3.14 ) is (2018)(a) 0.3
(b) 0.2
(c) 0.25
(d) 0.4
Ans: (a)
Sol:
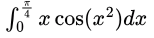 put x2 = t
put x2 = t2xdx = dt
t will range from 0 to π2/16
Now our new integral is :
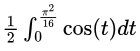
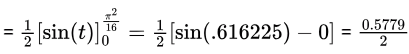 sin(.616225 radians) = 0.5779586366
sin(.616225 radians) = 0.5779586366= 0.289.
Q12: Which one of the following is a closed form expression for the generating function of the sequence {an}, where an = 2n+3 for all n = 0, 1, 2,...? (2018)
(a)
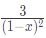
(b)
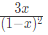
(c)
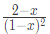
(d)
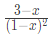
Ans: (d)
Sol: Given that an = 2n+3
Let G(x) be the generating function for the sequence {an}.
So,
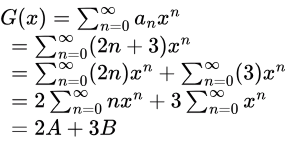 Now,
Now, 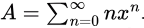 By expanding, it will look like:
By expanding, it will look like:0 + 1x + 2x2 + 3x3 +… which is an AGP series with first term, (a) = 0, common difference, (d) = 1, ratio, (r) = x.
Sum of infinite AGP series
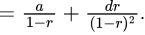
So,
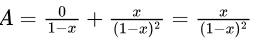
and
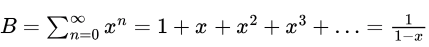
Therefore,
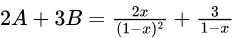
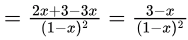 Option (D) is correct.
Option (D) is correct.Q13: If a random variable X has a Poisson distribution with mean 5, then the expectation E[(X + 2)2] equals ________. (2017 SET-2)
(a) 49
(b) 25
(c) 54
(d) 64
Ans: (c)
Sol: In Poisson distribution :
Mean = Variance as n is large and p is small
And we know:
Variance = E(X2) − [E(X)]2
⇒ E(X2) = [E(X)]2 + Variance
⇒ E(X2) = 52+5
⇒ E(X2) = 30
So, by linearity of expectation,
= E(X2) + 4E(X) + 4
= 30 + (4 x 5) + 4
= 54
Q14: If
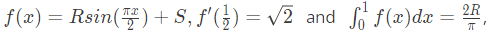 then the constants R and S are, respectively (2017 SET-2)
then the constants R and S are, respectively (2017 SET-2)(a)

(b)
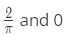
(c)
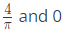
(d)
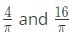
Ans: (c)
Sol: Correct Option: C.
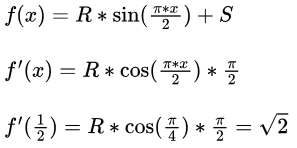
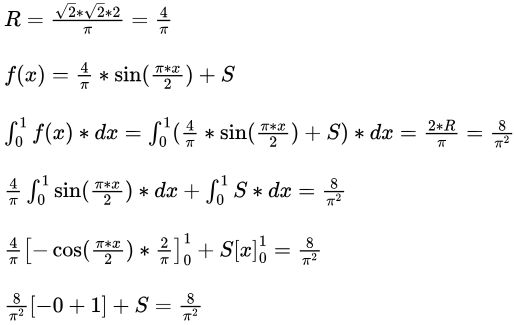 S = 0.
S = 0.Q15: Let u and v be two vectors in R2 whose Euclidean norms satisfy ||u||=2|| v|| . What is the value of α such that w = u + αv bisects the angle between u and v ? (2017 SET-1)
(a) 2
(b) 1/2
(c) 1
(d) -1/2
Ans: (a)
Sol: Angle between u and w = Angle between w and v
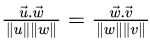
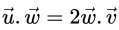
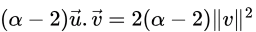 LHS and RHS would be equal for α = 2. Hence, correct answer is (A).
LHS and RHS would be equal for α = 2. Hence, correct answer is (A).Q16: The value of
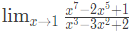 (2017 SET-1)
(2017 SET-1)(a) is 0
(b) is -1
(c) is 1
(d) does not exist
Ans: (c)
Sol: Since substituting x = 1 we get 0/0 which is indeterminate.
After applying L'Hospital rule, we get
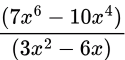
Now substituting x = 1 we get (-3/-3) = 1.
Hence, answer is 1.
Q17:
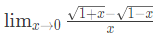 is given by (2016)
is given by (2016)(a) 0
(b) -1
(c) 1
(d) 1/2
Ans: (c)
Sol:
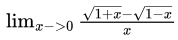 [putting x=0, it comes 0/0 form , So, apply L hospital rule(differentiate upper limit and lower limit differently)]
[putting x=0, it comes 0/0 form , So, apply L hospital rule(differentiate upper limit and lower limit differently)]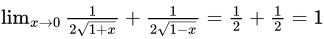
Q18: Which one of the following well-formed formulae in predicate calculus is NOT valid? (2016 SET-2)
(a) (∀xp(x) ⇒ ∀xq(x)) ⇒ (∃x¬p(x) ∨ ∀xq(x))
(b) (∃xp(x) ∨ ∃xq(x)) ⇒ ∃x(p(x) ∨ q(x))
(c) ∃x(p(x) ∧ q(x)) ⇒ (∃xp(x) ∧ ∃xq(x))
(d) ∀x(p(x) ∨ q(x)) ⇒ (∃xp(x) ∨ ∃xq(x))
Ans: (d)
Sol: Here, (D) is not valid
Let me prove by an example
What (D) is saying here is:
For all x ( x is even no or x is odd no ) ⇒ For all x ( x is even no ) or For all x ( x is odd no)
OR
If every x is either even or odd, then every x must be even or every x must be odd.
If our domain is the set of natural numbers LHS is true but RHS is false as not all natural numbers are even or odd.
Answer is (D).
Q19: Let f(x) be a polynomial and g(x) = f'(x) be its derivative. If the degree of (f(x)+ f(-x)) is 10, then the degree of (g(x)-g(-x)) is ________. (2016 SET-2)
(a) 10
(b) 9
(c) 11
(d) 8
Ans: (b)
Sol: Let f(x) = x10 Degree = 10.
f(x) + f(-x) = x10 + (-x)10
= x10+x10
= 2.x10
g(x) − g(−x) = 10.x9 − {−10x9}
= 20.x9
So, answer is 9.
Q20:
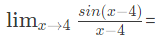 ____. (2016 SET-1)
____. (2016 SET-1)(a) 0
(b) 1
(c) 2
(d) 4
Ans: (b)
Sol:
Substitute h = x − 4, it becomes
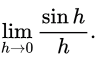
This is a standard limit and answer is 1.
Q21: If for non-zero x, af(x) + bf(1/x) = (1/x) −25 where a ≠ b then
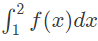 is (2015 SET-3)
is (2015 SET-3)(a)
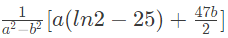
(b)
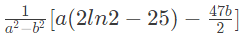
(c)
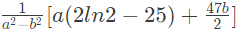
(d)
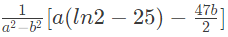
Ans: (a)
Sol: af(x) + bf(1/x) = (1/x) - 25 ...(1)
Integrating both sides,
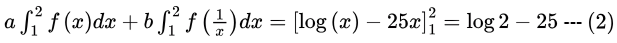 Replacing x by 1/x in (1), we get
Replacing x by 1/x in (1), we getaf(1/x) + bf(x) = x - 25
Integrating both sides, we get
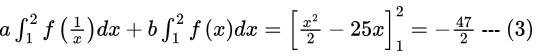 Eliminate
Eliminate 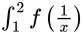 between (2) and (3) by multiplying (2) by a and (3) by b and subtracting
between (2) and (3) by multiplying (2) by a and (3) by b and subtracting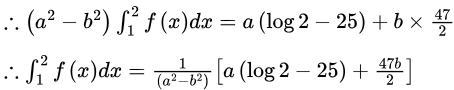 Answer: A.
Answer: A. 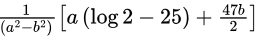
Q22: The value of
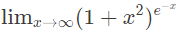 is (2015 SET-3)
is (2015 SET-3)(a) 0
(b) 1/2
(c) 1
(d) ∞
Ans: (c)
Sol: Apply an exponential of a logarithm to the expression.
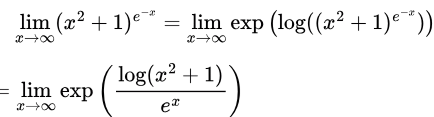 Since the exponential function is continuous, we may factor it out of the limit.
Since the exponential function is continuous, we may factor it out of the limit.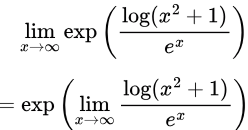 The numerator of e−x log(x2+1) grows asymptotically slower than its denominator as x approaches ∞.
The numerator of e−x log(x2+1) grows asymptotically slower than its denominator as x approaches ∞.Since log(x2 + 1) grows asymptotically slower than ex as x approaches ∞,
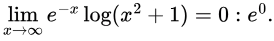
Evaluate e0.
e0 = 1:
Answer: 1.
Correct Answer: C
Q23: Let f(x) = x−(1/3) and A denote the area of the region bounded by f(x) and the x-axis, when x varies from -1 to 1. Which of the following statements is/are TRUE?
(I) f is continuous in [-1, 1]
(II) f is not bounded in [-1, 1]
(III) f is nonzero and finite
(a) II only
(b) III only
(c) II and III only
(d) I, II and III
Ans: (c)
Sol: I. f is continuous in [−1, 1]
Given,
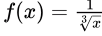
We need to check continuity at x = 0.
Left hand limit
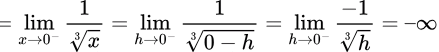
Right hand limit
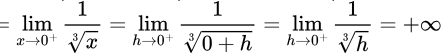
∴ LHL ≠ RHL
So, f is not continuous in [−1, 1]. Statement I is FALSE.
II. f is not bounded in [−1, 1]
Since at x = 0, f(x) goes from −∞ to +∞, f is not bounded at [−1, 1]. Statement II is TRUE.
III. A is non zero and finite.
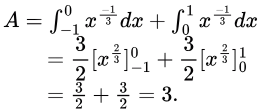 ∴ A is non-zero and finite. Statement III is TRUE.
∴ A is non-zero and finite. Statement III is TRUE.Answer: C
Q24:
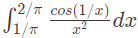 = ____. (2015 SET-1)
= ____. (2015 SET-1)(a) 0
(b) 1
(c) -1
(d) 0.5
Ans: (c)
Sol: For the integrand
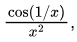 substitute u = 1/x and du = −1/x2 dx.
substitute u = 1/x and du = −1/x2 dx.This gives a new lower bound
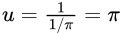 and upper bound
and upper bound 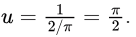
Now, our integral becomes:
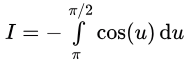
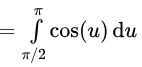
Since the antiderivative of cos(u) is sin(u), applying the fundamental theorem of calculus, we get:
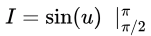 = sin(π) - sin(π/2)
= sin(π) - sin(π/2)= 0 - 1
= -1
Q25:
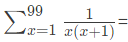 ____. (2015 SET-1)
____. (2015 SET-1)(a) 0.1
(b) 0.3
(c) 0.66
(d) 0.99
Ans: (d)
Sol:
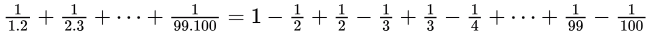 = 1 - (1/100)
= 1 - (1/100)Q26: limx→∞x1/x is (2015 SET-1)
(a) ∞
(b) 0
(c) 1
(d) Not defined
Ans: (c)
Sol: Apply an exponential of a logarithm to the expression.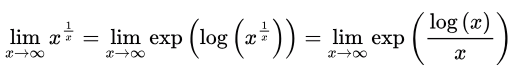 Since the exponential function is continuous, we may factor it out of the limit.
Since the exponential function is continuous, we may factor it out of the limit.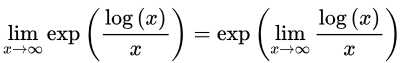
Since log(x) grows asymptotically slower than the polynomial x as x approaches ∞,
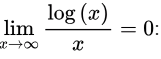
e0 = 1
Q27: What is the median of data if its mode is 15 and the mean is 30? (2014)
(a) 30
(b) 25
(c) 22.5
(d) 27.5
Ans: (b)
Sol: 3median = mode + 2mean
⇒ 3x = 15 + 60
⇒ 3x = 75
⇒ x = 75/3 = 25
Q28: The value of the integral given below is 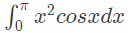 (2014 SET-3 )
(2014 SET-3 )
(a) -2π
(b) π
(c) -π
(d) 2π
Ans: (a)
Sol: 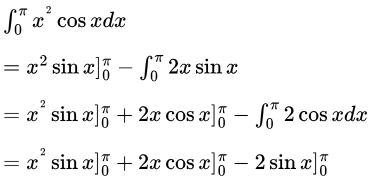 = [π2(0) - 0] + 2[π(-1) - 0] - 2[0 - 0]
= [π2(0) - 0] + 2[π(-1) - 0] - 2[0 - 0]
= -2π
Integral of a multiplied by b equals a multiplied by integral of b minus integral of derivative of a multiplied by integral of b
Q29: If 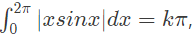 then the value of k is equal to _______. (2014 SET-3)
then the value of k is equal to _______. (2014 SET-3)
(a) 2
(b) 4
(c) 6
(d) 8
Ans: (b)
Sol: There is a mod term in the given integral. So, first we have to remove that. We know that x is always positive here and sinx is positive from 0 to π. From π to 2π, x is positive while sinx changes sign. So, we can write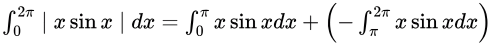
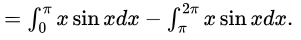
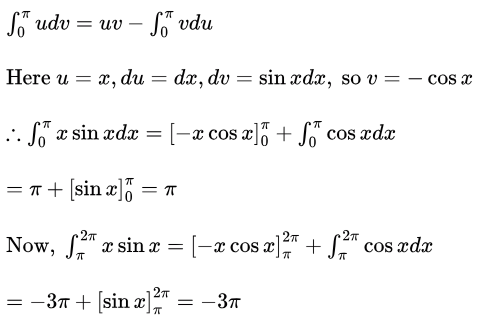 So, given integral = π − (−3π) = 4π
So, given integral = π − (−3π) = 4π
So, k = 4.
Q30: The function f(x) = xsinx satisfies the following equation: f′′(x) + f(x) + tcosx = 0. The value of t is______. (2014 SET-1)
(a) 2
(b) 1
(c) -2
(d) -1
Ans: (c)
Sol: f″(x) = xcos(x) + sin(x)
f″(x) = x(−sinx) + cosx + cosx
now f″(x) + f(x) + tcosx = 0
⇒ x(−sinx) + cosx + cosx + xsinx + tcosx = 0
⇒ 2cosx + tcosx = 0
⇒ cosx(t+2) = 0
⇒ t + 2 = 0, t = −2.
Q31: Let the function 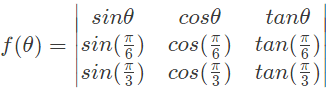 where
where 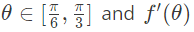 denote the derivative of f with respect to θ . Which of the following statements is/are TRUE? (2014 SET-1)}
denote the derivative of f with respect to θ . Which of the following statements is/are TRUE? (2014 SET-1)}
(I) There existrs 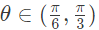 such that f′(θ) = 0
such that f′(θ) = 0
(I) There existrs 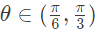 such that f′(θ) ≠ 0 (2014 SET-1)
such that f′(θ) ≠ 0 (2014 SET-1)
(a) I only
(b) II only
(c) Both I and II
(d) Neither I nor II
Ans: (c)
Sol: We need to solve this by Rolle's theorem. To apply Rolle's theorem following 3 conditions should be satisfied:
- f(x) should be continuous in interval [a, b],
- f(x) should be differentiable in interval (a, b), and
- f(a) = f(b)
For the given question, it satisfies all the three conditions, so we can apply Rolle's theorem, i.e, there exists at least one θ that gives f′(θ) = 0
Also, the given function is also not a constant function, i.e., for some θ, f′(θ) ≠ 0
So, answer is C.
Q32: What is the least value of the function f(x) = 2x2−8x−3 in the interval [0, 5]? (2013)
(a) -15
(b) 7
(c) -11
(d) -3
Ans: (c)
Sol: f(x) = 2x2 - 8x - 3
f′(x) = 4x − 8
For stationary point: f′(x) = 0 ⇒ 4x − 8 = 0 ⇒ x = 2
Therefore, critical points x = 0, 2, 5
Now, f″(x) = 4 > 0(Minima)
For getting the minimum (or) least value , we should check all the value of critical points (stationary point and closed interval points).
For x = 0 : f(x) = −3
For x = 2 : f(x) = 8 − 16 − 3 = −11
For x = 5 : f(x) = 50 − 40 − 3 = 7
∴ x = 2,minimum value of f(x) = −11
So, the correct answer is (c).
Q33: Which one of the following functions is continuous at x = 3? (2013)
(a) 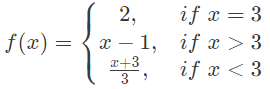 (b)
(b) 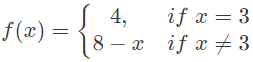 (c)
(c) 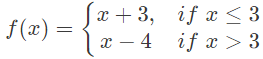 (d)
(d) 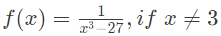 Ans: (a)
Ans: (a)
Sol: For continuity, Left hand limit must be equal to right hand limit. For continuity at x = 3,
the value of f(x) just above and just below 3 must be the same.
- f(3) = 2.f(3+) = x − 1 = 2. f(3−) =
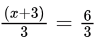 = 2. Hence, continuous.
= 2. Hence, continuous. - f(3) = 4.f(3+) = f(3−) = 8 − 3 = 5. So, not continuous.
- f(3) = f(3−) = x+3 = 6.f(3+) = x − 4 = −1. So, not continuous.
- f(3) is not existing. So, not continuous.
Q34: Consider the function f(x) = sin(x) in the interval x ∈ [π/4, 7π/4]. The number and location(s) of the local minima of this function are (2012)
(a) One, at π/2
(b) One, at 3π/2
(c) Two, at π/2 and 3π/2
(d) Two, at π/4 and 3π/2
Ans: (d)
Sol: f′(s) = cosx = 0 gives root π/2 and 3π/2 which lie between the given domain in question 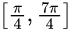
f" (x) = - sinx at π/2 gives −1 < 0 which means it is local maxima and at 3π/2 it gives 1>0 which is local minima.
Since, at π/2 it is local maxima so, before it, graph is strictly increasing, so π/4 is also local minima.
So, there are two local minima π/4 and 3π/2.
Q35: n-th derivative of xn is (2011)
(a) nxn-1
(b) nn.n!
(c) nxn!
(d) n!
Ans: (d)
Sol: f(x) = xⁿ
f'(x) = n x(n-1)
f''(x) = n(n-1) x(n-2)
f''(x) = n(n-1)(n-2) x(n-3)
fⁿ(x) = n! x(n-n) , and since n - n = 0, x0 = 1,
so fⁿ(x) = n!
Hence,Option (D)n! is the correct choice.
Q36: Given i = √-1, what will be the evaluation of the definite integral 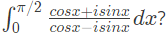 (2011)
(2011)
(a) 0
(b) 2
(c) i
(d) -i
Ans: (c)
Sol: 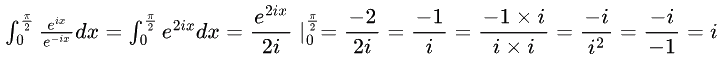
Q37: The weight of a sequence a0, a1,...,an−1 of real numbers is defined as a0 + a1/2 + ... + an−1/2n−1 A subsequence of a sequence is obtained by deleting some elements from the sequence, keeping the order of the remaining elements the same. Let X denote the maximum possible weight of a subsequence of a0, a1 ,..., an−1. Then X is equal to (2010)
(a) max(Y, a0 + Y)
(b) max(Y, a0 + Y/2)
(c) max(Y, a0 + 2Y)
(d) a0 + Y/2
Ans: (b)
Sol: S = ⟨a0, S1⟩
S1 = ⟨a1, a2, a3 ... an-1⟩
- a0 is included in the max weight subsequence of S:
In this case, X = weight (⟨a0, S1⟩) = a0 + (Y/2) - a0 is not included in the max weight subsequence of S:
In this case, X = weight (S1) = Y
The maximum possible weight of a subsequence of S is given by:
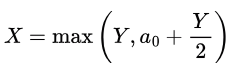 Thus, option B is correct.
Thus, option B is correct.Q38: What is the value of lim n→∞(1−(1/n))2n? (2010)
(a) 0
(b) e-2
(c) e-1/2
(d) 1
Ans: (b)
Sol: I will solve by two methods
Method 1: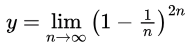 Taking log
Taking log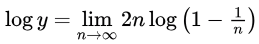
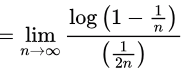 (converted this so as to have form (0/0) )
(converted this so as to have form (0/0) )
Apply L' hospital rule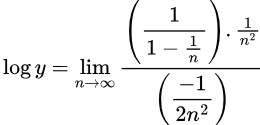 log y = -2
log y = -2
y = e-2.
Method 2:
It takes 1 to power infinity form 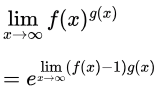 where,
where, 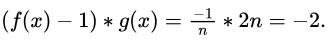
i.e., -2 constant.
so we get final ans is = e-2.
|
34 videos|123 docs|72 tests
|
FAQs on Previous Year Questions: Calculus - Engineering Mathematics for Computer Science Engineering - Computer Science Engineering (CSE)
| 1. How can calculus be applied in computer science engineering? |  |
| 2. What are some common applications of calculus in computer science engineering? |  |
| 3. How does calculus play a role in machine learning and artificial intelligence? |  |
| 4. Can calculus help in analyzing big data in computer science engineering? |  |
| 5. How can understanding calculus concepts improve problem-solving skills in computer science engineering? |  |
|
34 videos|123 docs|72 tests
|

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|














