Previous Year Questions: Relational Schema | Database Management System (DBMS) - Computer Science Engineering (CSE) PDF Download
Q1: The symbol → indicates functional dependency in the context of a relational database. Which of the following options is/are TRUE? (2024 SET 1)
(a) ( X , Y ) → ( Z , W ) implies X → ( Z , W )
(b) ( X , Y ) → ( Z , W ) implies ( X , Y ) → Z
(c) ( ( X , Y ) → Z and W → Y ) implies ( X , W ) → Z
(d) ( X → Y and Y → Z ) implies X → Z
Ans: (b, c, d)
Sol: Correct Answer - Option B,C,D
Option B - Decomposition rule of functional dependencies.
Option C - Apply augmentation rule with X on W -> Y, Then apply Transitivity rule to get X, W -> Z.
Option D - Definition of Transitivity rule for functional dependencies
Q2: Which one of the options given below refers to the degree (or arity) of a relation in relational database systems? (2023)
(a) Number of attributes of its relation schema.
(b) Number of tuples stored in the relation.
(c) Number of entries in the relation.
(d) Number of distinct domains of its relation schema.
Ans: (a)
Sol: Relational Model Definitions:
A relation is a table with columns and rows.
An attribute is a named column of a relation.
A tuple is a row of a relation.
A domain is a set of allowable values for one or more attributes.
The degree of a relation is the number of attributes it contains.
The cardinality of a relation is the number of tuples it contains.
A relational database is a collection of normalized relations with distinct relation names.
The intension of a relation is the structure of the relation including its domains.
The extension of a relation is the set of tuples currently in the relation.
Q3: Consider a relation R ( A , B , C , D , E ) R with the following three functional dependencies.
A B → C ; B C → D ; C → E ;
The number of superkeys in the relation R is . (2022)
(a) 12
(b) 8
(c) 6
(d) 5
Ans: (b)
Sol: AB → C
BC → D
C → E
are the FDs in the question. If you observe the given FD set, A and B are Independent attributes.
∴ every key must contain A and B
Let’s compute Keys of the relations :
(AB) + = ABCDE
Independent Attributes form the Key, then It is unique and minimal candidate key.
There are 3 more attributes in the given relation, So adding them to Candidate Key results Super key.
Every attribute has two choices (either add to candidate key or left it), and there are 3 such attributes
∴ No. of super keys = 2. 2. 2 = 8
Note that Every candidate Key is also Super Key.
Q4: Consider the following statements S1 and S2 about the relational data model: (2021 SET 2)
S1: A relation scheme can have at most one foreign key.
S2: A foreign key in a relation scheme R cannot be used to refer to tuples of R.
Which one of the following choices is correct?
(a) Both S1 and S2 are true
(b) S1 is true and S2 is false
(c) S1 is false and S2 is true
(d) Both S1 and S2 are false
Ans: (d)
Sol: Both S 1 and S 2 are FALSE
In a relation scheme multiple foreign attributes can be present referring to primary keys of other relation schemes. A typical example is an EXAM_RESULTS(sid, eid, marks) scheme where sid and eid are foreign keys referring to the primary keys in STUDENT and EXAM schemes respectively.
S 2 is FALSE because a foreign key can refer to the same scheme (self-referencing foreign key). A typical example is an EMPLOYEE(eid, mid, … ) scheme where mid is the Manager ID referring to the primary key eid of the same scheme.
Q5: Consider the relation R ( P , Q , S , T , X , Y , Z , W ) with the following functional dependencies. (2021 SET 1)
P Q → X ; P → Y X ; Q → Y ; Y → Z W
Consider the decomposition of the relation R into the constituent relations according to the following two decomposition schemes.
D 1 : R = [ ( P , Q S , T ) ; ( P , T , X ) ; ( Q , Y ) ; ( Y , Z , W ) ]
D 2 : R = [ ( P , Q , S ) ; ( T , X ) ; ( Q , Y ) ; ( Y , Z , W ) ]
Which one of the following options is correct?
(a) D1 is a lossless decomposition, but D2 is a lossy decomposition.
(b) D1 is a lossy decomposition, but D2 is a lossless decomposition.
(c) Both D1 and D2 are lossless decompositions.
(d) Both D1 and D2 are lossy decompositions.
Ans: (a)
Sol: Lossless-Join Decomposition:
Decomposition of R into R1, R2, R3, R4 is a lossless-join decomposition if at least one of the following functional dependencies are in F+ (Closure of functional dependencies):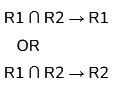
For decomposition D1:
R1(PQST)
R2(PTX)
R3(QY)
R4(YZW)
R1 ∩ R2 = (PT)+ = PTYXZW , it is a super key, so we can merge R1 and R2.
combined table T1 is PQSTX
similarly,
R3 ∩ R4 =(Y)+ = YZW, it is a super key, so we can merge R3 and R4.
another combined table T2 is QYZW.
now, Q is common in both T1 and T2.
T1 ∩ T2 = Q+ = QYZW, it is a super key, so we can merge T1 and T2.
after combining, we get original table PQSTXYZW,
Hence D1 is lossless join decomposition.
For decomposition D2:
R1(PQS)
R2(TX)
R3(QY)
R4(YZW)
since R2 has no common attributes as the primary key, so R2 cannot be merge with any other table,
Hence D2 is lossy decomposition.
Q6: Which of the following is NOT a superkey in a relational schema with attributes V, W, X, Y, Z and primary key V Y? (2016 SET 1)
(a) VXYZ
(b) VWXZ
(c) VWXY
(d) VWXYZ
Ans: (b)
Sol: Option A VXYZ So VY is Part of it Correct
Option B VWXZ SO No VY is Subset It Fails It Incorrect
Option C VWXY So VY is Part o f it Correct
Option D VWXYZ So VY is Part of it it Also Correct
Answer Is B
Q7: Given an instance of the STUDENTS relation as shown below (2014 SET 2)
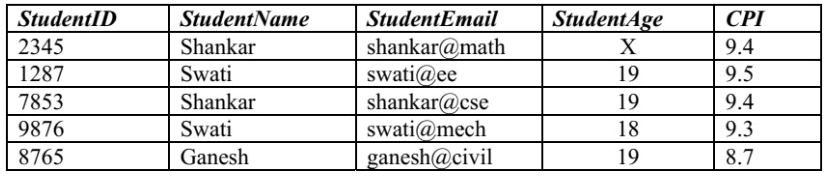
For (StudentName, StudentAge) to be a key for this instance, the value x should NOT be equal to_______.
(a) 18
(b) 19
(c) 9.4
(d) 7853
Ans: (b)
Sol: Should not eqaul to 19.
Since if it is equal the same key will have two different values for "StudentEmail" which cannot be true by the definition of candidate/primary/super key.
Q8: The maximum number of super keys for the relation schema R (E, F, G, H) with E as the key is __________. (2014 SET 2)
(a) 32
(b) 16
(c) 8
(d) 4
Ans: (c)
Sol: Super Key is any set of attributes that uniquely determines a tuple in a relation.
Since E is the only key, E should be present in any super key.
Excluding E , there are three attributes in the relation, namely F , G , H . Hence, if we add E to any subset of those three attributes, then the resulting set is a super key. Number of subsets of { F , G , H } is 8 . Hence the answer is 8 .
The following are Super Keys:

Q9: Consider the relation scheme R = (E, F, G, H, I, J, K, L, M, N) and the set of functional dependencies (2014 SET 1)
{{E,F} → →{G}, {F} → →{I,J}, {E,H} → →{K,L}, {K} → →{M}, {L} → →{N} } on R. What is the key for R?
(a) {E, F}
(b) {E, F, H}
(c) {E, F, H, K, L}
(d) {E}
Ans: (b)
Sol: Since E , F , H cannot be derived from anything else E , F , H should be there in key.
Using Find { E F H } + , it contains all the attributes of the relation.
Hence, it is key.
Correct Answer: B
Q10: Consider a relational table with a single record for each registered student with the following attributes. (2011)
1. Registration_Number: Unique registration number for each registered student
2. UID: Unique Identity number, unique at the national level for each citizen
3. BankAccount_Number: Unique account number at the bank. A student can have multiple accounts or joint accounts. This attributes stores the primary account number
4. Name: Name of the Student
5. Hostel_Room: Room number of the hostel
Which of the following options is INCORRECT?
(a) BankAccount_Number is a candidate key
(b) Registration_Number can be a primary key
(c) UID is a candidate key if all students are from the same country
(d) If S S is a superkey such that S ∩ UID S∩UID is NULL then S ∪ UID S∪UID is also a superkey
Ans: (a)
Sol: Answer is (A)
A relation is given (Registration_Num, UID, BankAccount_Num, Name, Hostel_Room).
Now, Registration_Num is unique for each student. So with this, we can identify each student. Hence, this can be the primary key.
UID: It's an identification number for a person in a country. ( Say you're in India and your UID is 0243. Someone in Pakistan may also have the same UID as 0243 ) . So, if all students are from India (that is, the same country) then their UID will be different and then UID will be a Candidate key.
If S is a super key then S ∪ UID will be a Super key. e.g. R(A, B, C, D), If AB is a superkey then ABC, ABCD are also superkey. BankAccount_Num is not a candidate key, because a student can have multiple accounts or joint accounts. We can not identify each student uniquely with BankAccount_Num.
Q11: The following functional dependencies are given: (2006)
A B → C D , A F → D , D E → F , C → G , F → E , G → A
Which one of the following options is false?
(a) { C F } * = { A C D E F G }
(b) { B G } * = { A B C D G }
(c) { A F } * = { A C D E F G }
(d) { A B } * = { A B C D G }
Ans: (c)
Sol: Option A: { C F } ∗ = { A C D E F G }
=> {C F} * =  +
+
=> {C F} * = {C G A F D E}
If we just rearrange the terms:
{ C F } * = { A C D E F G }
Hence True
{B G} * = { A B C D G }
=> {B G} * 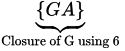 +
+ 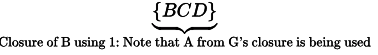
=> {B G} * = {G A B C D}
If we just rearrange the terms:
=> { C F } * = { A C D E F G }
Hence True
Option C: { A F } *= { A C D E F G }
= > { A F } * =  +
+
= > { A F } * = { A D E F }
If we just rearrange the terms:
= > { A F } *= { A C D E F G }
But this is not equal to { A F } *= { A C D E F G }
Hence False
Option D: { A B } * = { A B C D G }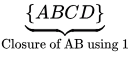 +
+ 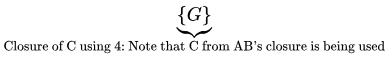
= > { A B } * = { A B C D G }
Hence True
Hence only False option C (Answer).
Q12: Consider a relation scheme R=(A,B,C,D,E,H) on which the following functional dependencies hold: {A → B, BC →D, E → C, D → A}. What are the candidate keys of R? (2005)
(a) AE, BE
(b) AE, BE, DE
(c) AEH, BEH, BCH
(d) AEH, BEH, DEH
Ans: (d)
Sol: using the given functional dependencies and looking at the dependent attributes, E and H are not dependent on any. So, they must be part of any candidate key. So, only option is D. If we see the FD's, adding A, B or D to EH do form candidate keys.
|
63 videos|93 docs|37 tests
|
















