Unit Test (Solutions): Quadratic Equations | Mathematics (Maths) Class 10 PDF Download
Time: 1 hour
M.M. 30
Attempt all questions.
- Question numbers 1 to 5 carry 1 mark each.
- Question numbers 6 to 8 carry 2 marks each.
- Question numbers 9 to 11 carry 3 marks each.
- Question number 12 & 13 carry 5 marks each.
Q1: Equation of (x+1)2-x2=0 has a number of real roots equal to: (1 Mark)
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (a)
(x+1)2-x2=0
x2+2x+1-x2 = 0
2x+1=0
x=-½
Hence, there is one real root.
Q2: The sum of two numbers is 27, and the product is 182. The numbers are: (1 Mark)
(a) 12 and 13
(b) 13 and 14
(c) 12 and 15
(d) 13 and 24
Ans: (b)
Let x is one number
Another number = 27 – x
Product of two numbers = 182
x(27 – x) = 182
⇒ x2 – 27x – 182 = 0
⇒ x2 – 13x – 14x + 182 = 0
⇒ x(x – 13) -14(x – 13) = 0
⇒ (x – 13)(x -14) = 0
⇒ x = 13 or x = 14
Q3: A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train. (1 Mark)
(a) 30 km/hr
(b) 40 km/hr
(c) 50 km/hr
(d) 60 km/hr
Ans: (b)
Let x km/hr be the speed of the train.
Time required to cover 360 km = 360/x hr.
As per the question given,
⇒ (x + 5)(360-1/x) = 360
⇒ 360 – x + 1800-5/x = 360
⇒ x2 + 5x + 10x – 1800 = 0
⇒ x(x + 45) -40(x + 45) = 0
⇒ (x + 45)(x – 40) = 0
⇒ x = 40, -45
Negative value is not considered for speed, hence the answer is 40km/hr.
Q4: A quadratic equation ax2 + bx + c = 0 has no real roots if _______________________________. (1 Mark)
Ans: b2 – 4ac < 0
A quadratic equation ax2 + bx + c = 0 has no real roots if b2 – 4ac < 0. That means the quadratic equation contains imaginary roots.
Q5: The maximum number of roots for a quadratic equation is equal to (1 Mark)
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (b)
The maximum number of roots for a quadratic equation is equal to 2 since the degree of a quadratic equation is 2.
Q6: The sum of the areas of two squares is 468 m2. If the difference of their perimeters is 24cm, find the sides of the two squares. (2 Marks)
Ans:
Let the side of the larger square be x. Let the side of the smaller square be y.
x2+y2=468
Cond. II 4x-4y = 24
⇒ xy = 6
⇒ x = 6+y
⇒ x2 + y2 = 468
⇒(6+y)2 + y2 = 468
On solving, we get
y = 12
⇒ x = (12+6) = 18 m
∴ The lengths of the sides of the two squares are 18m and 12m.
Q7: If x =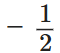 1 is a solution of the quadratic equation 3x2 + 2kx – 3 = 0, find the value of k. (2 Marks)
1 is a solution of the quadratic equation 3x2 + 2kx – 3 = 0, find the value of k. (2 Marks)
Ans:
The given quadratic equation can be written as, 3x2 + 2kx – 3 = 0 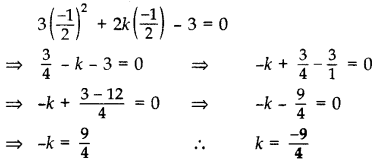
Q8: The product of two consecutive positive integers is 132. Find the integers. (2 Marks)
Ans:

Q9: Solve the quadratic equation 2×2 – 7x + 3 = 0 by using the quadratic formula. (3 Marks)
Ans:
2x2 – 7x + 3 = 0
On comparing the given equation with ax2 + bx + c = 0, we get,
a = 2, b = -7 and c = 3
By using the quadratic formula, we get,
x = [-b±√(b2 – 4ac)]/2a
⇒ x = [7±√(49 – 24)]/4
⇒ x = [7±√25]/4
⇒ x = [7±5]/4
Therefore,
⇒ x = 7+5/4 or x = 7-5/4
⇒ x = 12/4 or 2/4
∴ x = 3 or ½
Q10: Find two numbers whose sum is 30 and product is 200. (3 Marks)
Ans: Let the two numbers be x and y. We are given:
x+y(sum of the numbers)
xy (product of the numbers)
We can express in terms of from the first equation:
y = 30 − x
Substitute this into the second equation:
x (30 − x) = 200
30x x
xx
Now, solve the quadratic equation using the quadratic formula: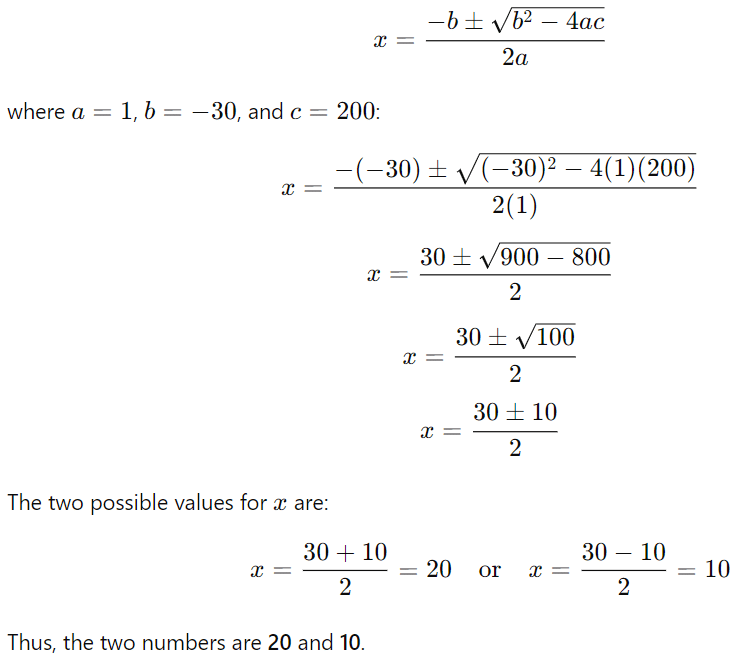
Q11: Find the roots of the following quadratic equations by factorization: (3 Marks)
(i) x2 + 7x + 10 = 0
(ii) 3x2 − 5x − 2 = 0
Ans:
(i) Solve x2 + 7x + 10 = 0
We need two numbers whose product is 10 and sum is 7. The numbers are 5 and 2 since and .
Rewrite the middle term:
xxx
Factorize by grouping:
x(x2(x
Factor out the common term:
(x+5)(x+2)
Thus, the roots are:
⇒ x =
⇒ x = −2
(ii) Solve 3x2−5x−2=0:
We need two numbers whose product is 3×(−2)=−6 and sum is -5. The numbers are -6 and 1 since and −6+1=−5.
Rewrite the middle term:
3x2 − 6x + x − 2 = 0
Factorize by grouping:
3x(x−2) + 1(x−2) = 0
Factor out the common term:
(3x+1) (x−2) = 0
Thus, the roots are: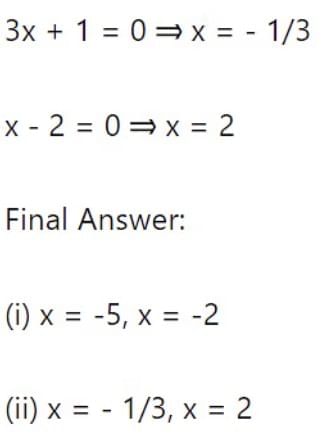
Q.12: A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was Rs.90, find the number of articles produced and the cost of each article. (5 Marks)
Ans:
Let the number of articles produced on that day be x. The cost of production of each article is 2x+3.
The total cost of production is given as:
xx
x
Using the quadratic formula: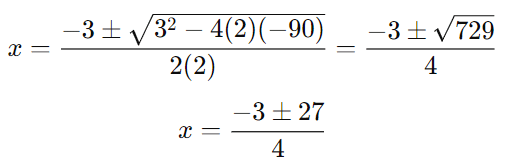
The two possible values of x are:
x (since the number of articles cannot be negative, discard x=−7.5)
The cost of production for each article is:
Thus, the number of articles produced is 6, and the cost of each article is Rs. 15.
Q13: The diagonal of a rectangular field is 60 meters more than the shorter side. If the longer side is 30 meters more than the shorter side, find the sides of the field. (5 Marks)
Ans: Let the shorter side of the rectangle be x meters.
Then, the diagonal of the rectangle is meters, and the longer side is meters.
According to the Pythagoras theorem:
(Diagonal)2 = (Shorter side)2 + (Longer side)2
Substituting the values:
(x+60)2= x2 +(x+30)2
Expanding both sides:
x2 x2 + x2 +60x +900
Simplifying:
x2
Bringing all terms to one side:
0 = x2 − 60x − 2700
Solve the quadratic equation:
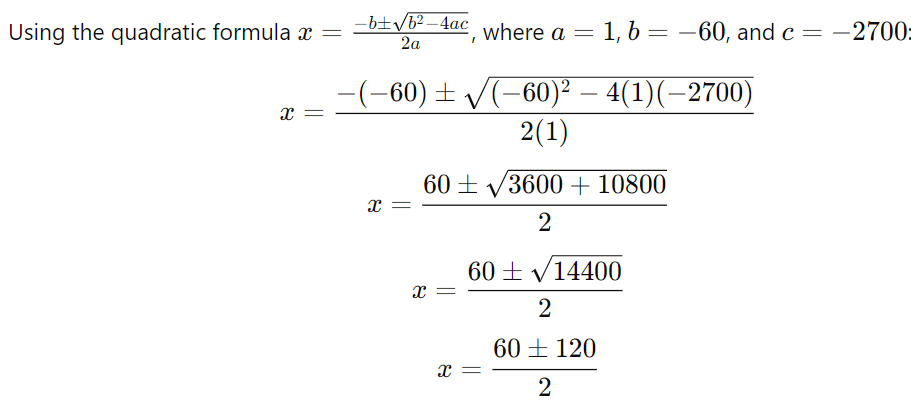
The two possible values for x are: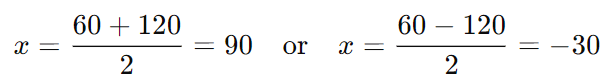
Since the length cannot be negative, we discard x = −30.
Thus,
The longer side is:
x
Thus, the shorter side is 90 meters and the longer side is 120 meters.
|
127 videos|584 docs|79 tests
|
FAQs on Unit Test (Solutions): Quadratic Equations - Mathematics (Maths) Class 10
| 1. What is the standard form of a quadratic equation? |  |
| 2. How do you factor a quadratic equation? |  |
| 3. What are the solutions to a quadratic equation called? |  |
| 4. What is the quadratic formula and when do you use it? |  |
| 5. How can you determine the number of real solutions a quadratic equation has? |  |
















