Unit Test (Solutions): Coordinate Geometry | Mathematics (Maths) Class 10 PDF Download

Time: 1 hour

M.M. 30

Attempt all questions.

• Question numbers 1 to 5 carry 1 mark each.
• Question numbers 6 to 8 carry 2 marks each.
• Question numbers 9 to 11 carry 3 marks each.
• Question number 12 & 13 carry 5 marks each.

Q1: If the distance between the points A(2, -2) and B(-1, x) is equal to 5, then the value of x is: (1 Mark)
(a) 2
(b) -2
(c) 1
(d) -1

Ans: (a)

By distance formula, we know:

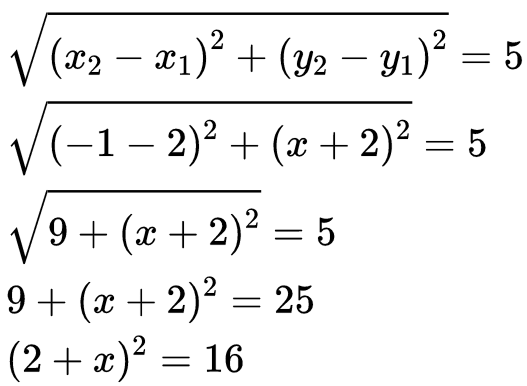
Take square root on both the sides,

2 + x = 4

x = 2

Q2: The midpoint of a line segment joining two points A(2, 4) and B(-2, -4) is (1 Mark)
(a) (-2, 4)
(b) (2, -4)
(c) (0, 0)
(d) (-2, -4)

Ans: (c)

As per midpoint formula, we know;

x-coordinate of the midpoint = [2 + (-2)]/2 = 0/2 = 0

y-coordinate of the midpoint = [4 + (-4)]/2=0/2=0

Hence, (0, 0) is the midpoint of AB.

Q3: The distance of point A(2, 4) from the x-axis is _______________________________. (1 Mark)

Ans: 4 units

The distance of a point from the x-axis is equal to the ordinate of the point.

Q4: If O(p/3, 4) is the midpoint of the line segment joining the points P(-6, 5) and Q(-2, 3), the  the value of p is: (1 Mark)
(a) 7/2
(b) -12
(c) 4
(d) -4

Ans: (b)

Since, (p/3, 4) is the midpoint of line segment PQ, thus;

p/3 = (-6-2)/2

p/3 = -8/2

p/3 = -4

p= -12

Therefore, the value of p is -12.

Q5: The ratio in which the line segment joining the points P(-3, 10) and Q(6, –8) is divided by O(-1, 6) is: (1 Mark)
(a) 1:3
(b) 3:4
(c) 2:7
(d) 2:5

Ans: (c)

Let k :1 be the ratio in which the line segment joining P( -3, 10) and Q(6, -8) is divided by point O(-1, 6).

By the section formula, we have;

-1 = ( 6k – 3)/(k + 1)

–k – 1 = 6k – 3

7k = 2

k = 2/7

Hence, the required ratio is 2:7.

Q6: Find a relation between x and y such that the point (x, y) is equidistant from the points (7, 1) and (3, 5). (2 Marks)

Ans: Let P(x, y) be equidistant from the points A(7, 1) and B(3, 5).

Then, AP = BP

AP² = BP²

Using distance formula,

(x – 7)² + (y – 1)² = (x – 3)² + (y – 5)²

x² – 14x + 49 + y² – 2y + 1 = x² – 6x + 9 + y² – 10y + 25

x – y = 2

Hence, the relation between x and y is x – y = 2.

Q7: The point A(3, y) is equidistant from the points P(6, 5) and Q(0, -3). Find the value of y. (2 Marks)

Ans: PA = QA …[Given]

PA2 = QA2 … [Squaring both sides]

(3 – 6)² + (y – 5)² = (3 – 0)² + (y + 3)²

9 + (y – 5)² = 9 + (y + 3)²

(y – 5)² = (y + 3)²

y – 5 =  ±(y + 3) … [Taking sq. root of both sides]

y – 5 = y + 3 y – 5 = -y – 3

0 = 8 … which is not possible ∴ y = 1

Q8: Name the type of triangle formed by the points A (–5, 6), B (–4, –2) and C (7, 5). (2 Marks)

Ans: The points are A (–5, 6), B (–4, –2) and C (7, 5).

Using distance formula,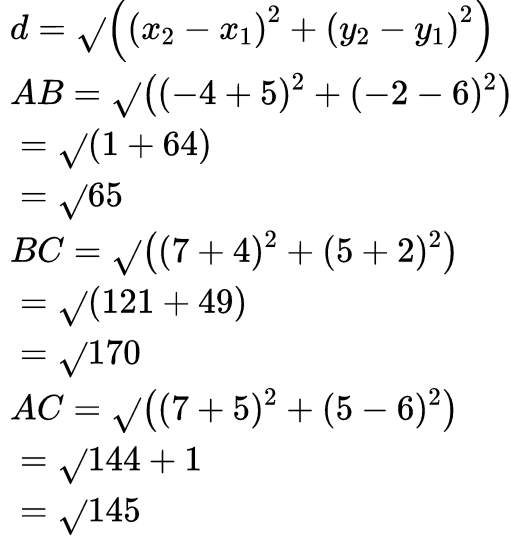
Since all sides are of different lengths, ABC is a scalene triangle. 

Q9: Three vertices of a parallelogram taken in order are (-1, 0), (3, 1) and (2, 2) respectively. Find the coordinates of fourth vertex. (3 Marks)

Ans: Let A(-1, 0), B(3, 1), C(2, 2) and D(x, y) be the vertices of a parallelogram ABCD taken in order. Since, the diagonals of a parallelogram bisect each other.

∴ Coordinates of the mid-point of AC = Coordinates of the mid-point of BD 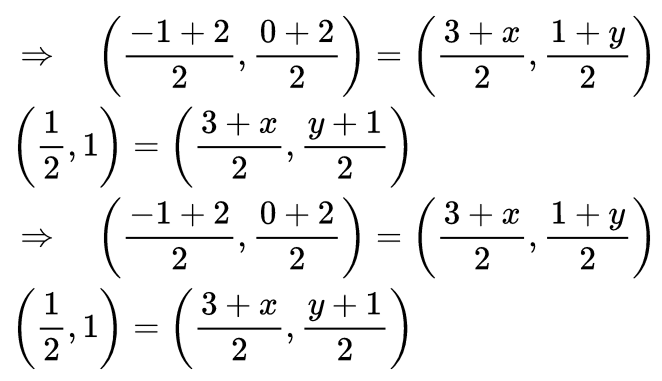Hence, coordinates of the fourth vertex, D(-2, 1). 

Q10: If the point P(k – 1, 2) is equidistant from the points A(3, k) and B(k, 5), find the values of k. (3 Marks)

Ans:

PA = PB …Given

PA² = PB² … [Squaring both sides]

⇒ (k – 1 – 3)² + (2 – k)² = (k – 1 – k)² + (2 – 5)²

⇒ (k – 4)² + (2 – k)² = (-1)² + (-3)²

k² – 8k + 16 + 4 + k² – 4k = 1 + 9

2k² – 12k + 20 – 10 = 0

2k² – 12k + 10 = 0

⇒ k² – 6k + 5 = 0 

⇒ k² – 5k – k + 5 = 0

⇒ k(k – 5) – 1(k – 5) = 0

⇒ (k – 5) (k – 1) = 0

⇒ k – 5 = 0 or k – 1 = 0

∴ k = 5 or k = 1

Q11: Prove that the points A(0, -1), B(-2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD. (3 Marks)

Ans: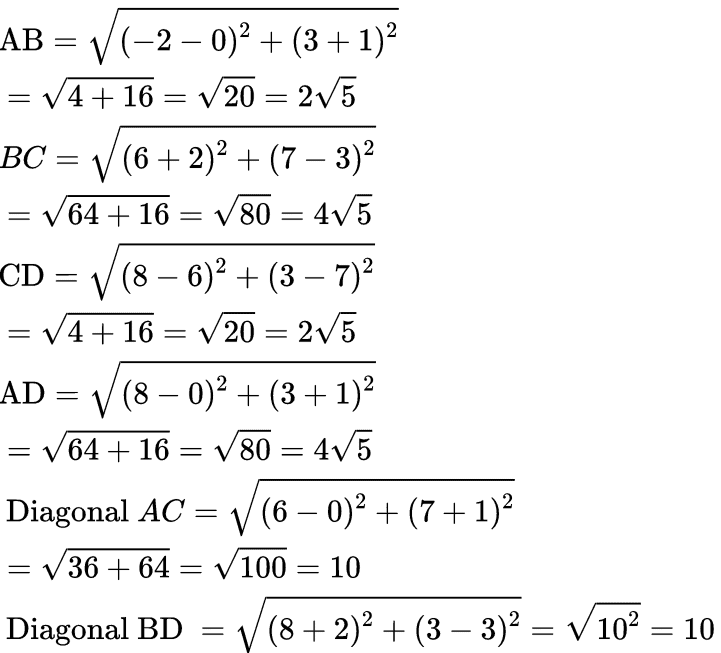 

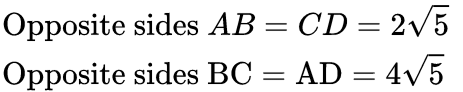
Diag. AC = BD = 10

∴ ABCD is a rectangle. … [∵ Opp. sides are equal & diagonals are also equal]

Q12: Find the ratio in which the line x – 3y = 0 divides the line segment joining the points (-2, -5) and (6, 3). Find the coordinates of the point of intersection. (5 Marks)

Ans: Let the given points be:

A(-2, -5) = (x1, y1)

B(6, 3) = (x2, y2)

The line x – 3y = 0 divides the line segment joining the points A and B in the ratio k:1.

Using section formula,

Point of division P(x, y) = [(kx² + x1)/(k + 1), (ky² + y1)/(k + 1)]

x = (6k – 2)/(k + 1) and y = (3k – 5)/(k + 1)

Here, the point of division lies on the line x – 3y = 0.

Thus,

[(6k – 2)/(k + 1)] – 3[(3k – 5)/(k + 1)] = 0

6k – 2 – 3(3k – 5) = 0

6k – 2 – 9k + 15 = 0

-3k + 13 = 0

-3k = -13

k = 13/3

Thus, the ratio in which the line x – 3y = 0 divides the line segment AB is 13 : 3.

Therefore, x = [6(13/3) – 2]/ [(13/3) + 1]

= (78 – 6)/(13 + 3)

= 72/16

= 9/2

And

y = [3(13/3) – 5]/ [(13/3) + 1]

= (39 – 15)/(13 + 3)

= 24/16

= 3/2

Therefore, the coordinates of the point of intersection = (9/2, 3/2).

Q13: Find the ratio in which P(4, m) divides the line segment joining the points A(2, 3) and B(6, -3). Hence, find m. (5 Marks)

Ans: Let P(4, m) divides the line segment joining the points A(2, 3) and B(6, -3) in the ratio k:1.

Here, P(4, m) = (x, y)

A(2, 3) = (x₁, y₁)

B(6, -3) = (x₂, y₂)

Using section formula,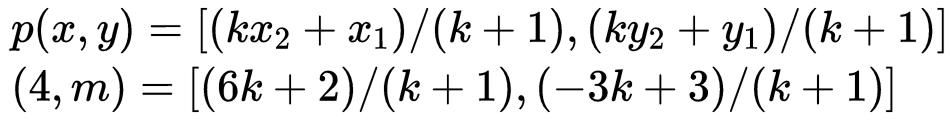

By equating the x-coordinate,

(6k + 2)/(k + 1) = 4

6k + 2 = 4k + 4

6k – 4k = 4 – 2

2k = 2

k = 1

Thus, the point P divides the line segment joining A and B in the ratio 1 : 1.

Now by equating the y-coordinate,

(-3k + 3)/(k + 1) = m

Substituting k = 1,

[-3(1) + 3]/(1 + 1) = m

m = (3 – 3)/2

m = 0