Maths Olympiad Previous Year Paper -1 | Mathematics Olympiad for Class 9 PDF Download
| Table of contents |

|
| Logical Reasoning |

|
| Mathematical Reasoning |

|
| Everyday Mathematics |

|
| Achievers Section |

|
Note: The questions provided in this document are similar to the questions that were asked in the actual Olympiad exam. So, we recommend you study these for your Olympiad preparation
Logical Reasoning
Q1: In the given Venn diagram, rectangle represents scientists, circle represents people worked in NASA and triangle represents people worked in ISRO. Which of the following number represents scientists who worked only in ISRO?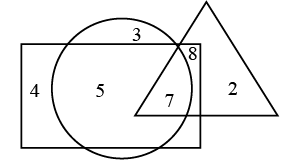 (a) 7
(a) 7
(b) 8
(c) 2
(d) 5
 View Answer
View Answer 
Ans: (b)
The number common to rectangle and triangle only is 8.
Q2: Identify the missing number in the following sequence:
4, 15, 48, 147, ?, 1335
(a) 364
(b) 441
(c) 426
(d) 444
 View Answer
View Answer 
Ans: (d)
- The pattern in the series involves multiplying the previous number by 3 and then adding 3.
- Starting with 4: 4 * 3 + 3 = 15.
- Next, 15: 15 * 3 + 3 = 48.
- Then, 48: 48 * 3 + 3 = 147.
- Continuing this, 147: 147 * 3 + 3 = 444, which is the missing number.
- Finally, 444: 444 * 3 + 3 = 1335, confirming the pattern.
Q3: There is a definite relationship between figures (i) and (ii). Establish a similar relationship between figures (iii) and (iv) by selecting a suitable figure from the options that would replace the (?) in fig. (iv).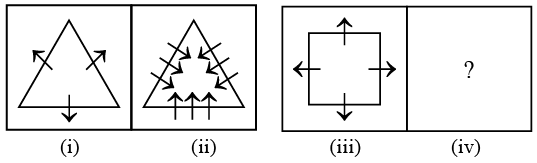 (a)
(a) 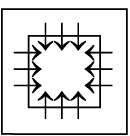
(b)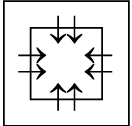
(c)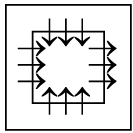
(d) 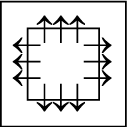
 View Answer
View Answer 
Ans: (a)
From figure (i) to (ii), the number of arrows is increased by two on each side and the direction of arrows get reversed.
Q4: How many pairs of letters are there in the word PRIMOGENITURE which have the same number of letters between them as in English alphabet?
(a) Nine
(b) Four
(c) Seven
(d) Ten
 View Answer
View Answer 
Ans: (d)
Q5: Vikrant walks 70 m to the East, then turns to his left and walks 60 m, then he turns left again and walks 20 m. Finally, he turns towards the right and walks 60 m. How far and in which direction is he now from the starting point?
(a) 120 m, South-West
(b) 130 m, North
(c) 130 m, North-East
(d) 120 m, South-East
 View Answer
View Answer 
Ans: (c)
- Vikrant starts by walking 70 m East.
- Then he turns left (to the North) and walks 60 m.
- Next, he turns left again (to the West) and walks 20 m.
- Finally, he turns right (to the North) and walks 60 m.
- After all these movements, he is 130 m away from the starting point in the North-East direction.
Q6: Select a figure from the options which satisfies the same conditions of placement of the dots as in the given figure.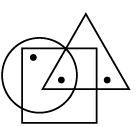 (a)
(a) 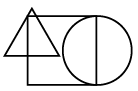
(b) 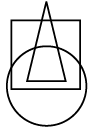
(c) 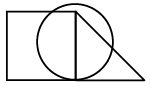
(d) 
 View Answer
View Answer 
Ans: (b)
Q7: Gaurav walks 20 metres towards North. He then turns left and walks 40 metres. He again turns left and walks 20 metres. Further, he moves 20 metres after turning to the right. How far is he from his original position?
(a) 20 metres
(b) 30 metres
(c) 50 metres
(d) 60 metres
 View Answer
View Answer 
Ans: (d)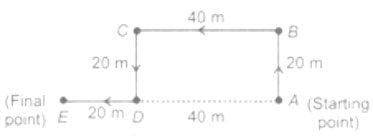 Hence, the distance from this original position i. e. A to E is (40 + 20) m = 60 m.
Hence, the distance from this original position i. e. A to E is (40 + 20) m = 60 m.
Q8: How many 7’s are there in the given series each of which is immediately preceded by an even number and immediately followed by 5?
6 4 7 5 8 1 7 5 2 7 6 7 5 3 9 7 4 7 8 7 5 6
(a) Two
(b) One
(c) Three
(d) Four
 View Answer
View Answer 
Ans: (c)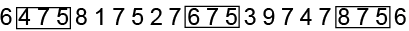
Q9: Six books P, Q, R, S, T and U are placed side by side. R, Q and T have blue covers and other books have red covers. Only S and U are new books and the rest are old, P, R and S are law reports, the rest are Gazetteers. Which two books are old Gazetteers with blue covers?
(a) Q and R
(b) Q and T
(c) Q and U
(d) T and U
 View Answer
View Answer 
Ans: (b)
Q10: If in a certain code language, GUIDELINES is written as GFKWIUGPKN, then how will SEPARATELY be written in the same code language?
(a) TBRHUANWCD
(b) UCRGVBNGVC
(c) TCRGUANGVC
(d) UBRIUBNHVC
 View Answer
View Answer 
Ans: (c)
- The code language involves a specific pattern of shifting letters. Each letter in the word is replaced by another letter based on a fixed rule.
- For example, in the word GUIDELINES, each letter is shifted to create GFKWIUGPKN.
- Applying the same shifting pattern to SEPARATELY, we find that it translates to TCRGUANGVC.
- This means that the correct answer is TCRGUANGVC, which corresponds to option (c).
Q11: If '@' represents '+', '©' represents '–', '$' represents '÷' and '#' represents '×', what is the result of 24©65$13@16#5?
(a) 99
(b) 87
(c) 109
(d) 61
 View Answer
View Answer 
Ans: (a)
- First, replace the symbols with their respective operations: 24 – 65 ÷ 13 + 16 × 5.
- Next, perform the division: 65 ÷ 13 = 5.
- Now, substitute back: 24 – 5 + 16 × 5.
- Then, perform the multiplication: 16 × 5 = 80.
- Finally, calculate: 24 – 5 + 80 = 19 + 80 = 99.
Q12: Find the number of triangles formed in the given figure.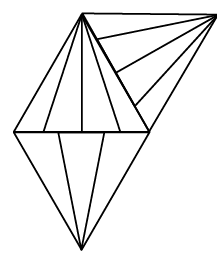 (a) 20
(a) 20
(b) 19
(c) 18
(d) More than 20
 View Answer
View Answer 
Ans: (d)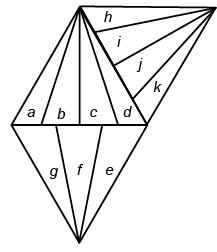 Triangles formed are : a, b, c, d, e, f, g, h, i, j, k, ab, bc, cd, gf, fe, hi, ij, jk, abc, bcd, gfe, hij, ijk, abcd and hijk i.e., 26 in number.
Triangles formed are : a, b, c, d, e, f, g, h, i, j, k, ab, bc, cd, gf, fe, hi, ij, jk, abc, bcd, gfe, hij, ijk, abcd and hijk i.e., 26 in number.
Q13: How many pairs of letters can be found in the word APPOINTMENT that have the same number of letters between them as they do in the English alphabet?
(a) None
(b) One
(c) Three
(d) Four
 View Answer
View Answer 
Ans: (d)
- To find the pairs of letters in the word APPOINTMENT, we need to check each letter and see if the number of letters between them in the word matches the number of letters between them in the alphabet.
- For example, the letters A and C have 1 letter between them in the alphabet, and they also have 1 letter between them in the word.
- After checking all possible pairs, we find that there are four such pairs: AP, IN, OT, and MT.
- Thus, the answer is Four pairs of letters.
Q14: Examine the information provided and respond to the following question: H % E * D $ G means what relationship does H have with G?
(a) Brother
(b) Father
(c) Mother
(d) Uncle
 View Answer
View Answer 
Ans: (b)
- First, let's break down the symbols: H % E means H is the father of E.
- Next, E * D indicates that E is the sister of D.
- Then, D $ G shows that D is the brother of G.
- Putting it all together, H is the father of E, who is the sister of D, and D is the brother of G. Therefore, H is the father of G.
Q15: How many pairs of letters are there in the word PRIMOGENITURE which have the same number of letters between them as in English alphabet?
(a) Nine
(b) Four
(c) Seven
(d) Ten
 View Answer
View Answer 
Ans: (d)
Mathematical Reasoning
Q16: Which of the following numbers lie on the face opposite to the face having number 6 when the given net is folded to form a cube?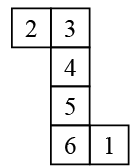
(a) 2
(b) 4
(c) 1
(d) 5
 View Answer
View Answer 
Ans: (b)
The numbers on opposite faces are: (1, 2), (3, 5) and (4, 6).
Q17: If x = 3 and y = –2 is a solution to the linear equation 3x – ky = 1, what is the value of k?
(a) 6
(b) –2
(c) 3
(d) –4
 View Answer
View Answer 
Ans: (d)
- To find the value of k, substitute x = 3 and y = –2 into the equation 3x – ky = 1.
- This gives us 3(3) – k(-2) = 1, which simplifies to 9 + 2k = 1.
- Rearranging this, we get 2k = 1 - 9, leading to 2k = -8.
- Dividing both sides by 2, we find k = -4.
Q18: Find the coordinates of the point which divides the line joining the points (8, 7) and (-9, 4) internally in the ratio 2 : 3.
(a) (1.8, 5.2)
(b) (2, 5)
(c) (1.2, 5.8)
(d) (2, 7)
 View Answer
View Answer 
Ans: (c)
Let the coordinates of the point of internal division A be (x, y). Then 
Q19: Determine the ratio in which 2x + 3y - 30 = 0 divides the line joining the points A (4, 5) and B (6, 7).
(a) 7 : 3
(b) 2 : 5
(c) 5 : 2
(d) 2 : 7
 View Answer
View Answer 
Ans: (a)
Let the line 2x + 3y - 30 = 0 divide the join of A (4,5) and B (6,7) at point C (p, q) in the ratio k: 1. Then,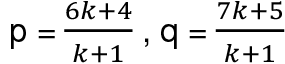
As the point C lies on the line 2x + 3y - 30 = 0, it satisfies the given equation, i.e,
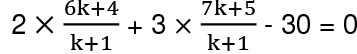
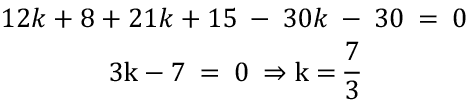
Q20: The perpendicular distance of a point from the x-axis is 5 units and its perpendicular distance from the y-axis is 7 units. Find the coordinates of the point if it lies in the Ill Quadrant.
a. (-7, -5)
b. (-5, -7)
c. (7, -5)
d. (-7, 5)
 View Answer
View Answer 
Ans: (a)
The perpendicular distance from the x-axis is y co-ordinate and vice versa So, x = 7, y = 5
In the III quadrant, both x and y are negative. Hence coordinates are (- 7, - 5)
Q21: Which smallest number must be added to 454189 to transform it into a perfect square?
(a) 68
(b) 92
(c) 87
(d) 58
 View Answer
View Answer 
Ans: (c)
- To find the smallest number to add to 454189 to make it a perfect square, we first need to determine the nearest perfect square greater than 454189.
- The square root of 454189 is approximately 673.5. The next whole number is 674.
- Calculating 674 squared gives us 454276. Now, we subtract 454189 from 454276.
- This results in 87, which is the smallest number that needs to be added to 454189 to achieve a perfect square.
Q22: If 2x + 3y = 6 and kx + 6y = 15 has a unique solution, then find the set of values of k.
(a) N
(b) N - {4}
(c) R
(d) R - {4}
 View Answer
View Answer 
Ans: (d)
Given, 2x + 3y = 6
kx + 6y = 15
The system has a unique solution,
i.e., 2/k ≠ 3/6
⇒ k ≠ 4
The value of k is any real number except 4.
Q23: A person can row 16 km upstream in 8 hours and 20 km downstream in 2 hours. Find the speed of the person in still water (in kmph).
(a) 12
(b) 8
(c) 6
(d) 4
 View Answer
View Answer 
Ans: (c)
Let the speed of the man in still water be x kmph and speed of the stream be y kmph 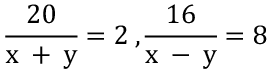
⇒ x + y = 10 (1)
⇒ x - y = 2 (2)
Eq. (1) + Eq. (2) ⇒ 2x = 12 ⇒ x = 6
Q24: If x + y + z = 1, xy + yz + zx = -1, and xyz = -1, what is the value of x3 + y3 + z3?
(a) –1
(b) 1
(c) 2
(d) –2
 View Answer
View Answer 
Ans: (b)
- To find the value of x3 + y3 + z3, we can use the identity: x3 + y3 + z3 = (x + y + z)(x2+ y2 + z2 - xy - yz - zx) + 3xyz.
- Given that x + y + z = 1 and xyz = -1, we need to calculate x² + y² + z².
- Using the formula x2 + y2 + z2 = (x + y + z)2 - 2(xy + yz + zx), we find x2 + y2 + z2 = 12 - 2(-1) = 1 + 2 = 3.
- Now substituting these values into the identity gives us: x3 + y3 + z3 = 1(3 - (-1)) + 3(-1) = 1(4) - 3 = 4 - 3 = 1.
Q25: The number of faces in a polyhedron is 5, and the total number of vertices is two-thirds of the total number of edges. Find the total number of vertices.
(a) 8
(b) 9
(c) 12
(d) 6
 View Answer
View Answer 
Ans: (d)
- We know that a polyhedron has 5 faces.
- Let the number of edges be E and the number of vertices be V.
- According to the problem, V = (2/3)E.
- Using Euler's formula for polyhedra, which states V - E + F = 2, we can substitute F = 5.
- This gives us the equation: V - E + 5 = 2, or V - E = -3.
- Now, substituting V from the earlier equation, we get: (2/3)E - E = -3.
- This simplifies to (-1/3)E = -3, leading to E = 9.
- Now substituting E back to find V: V = (2/3) * 9 = 6.
- Thus, the total number of vertices is 6.
Q26: In ∆HIJ, K and L are on HI and HJ, respectively, such that KL || IJ. If HK = 3p - 2, KI = 2p + 7 and HL : LJ = 2 : 3, then the value of p is _______.
(a) 2
(b) 3
(c) 1
(d) 4
 View Answer
View Answer 
Ans: (d)
Using the basic proportionality theorem, 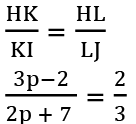
⇒ 9p - 6 = 4p + 14
⇒ p = 4
Q27: Things which are equal to the same thing are ______ to one another.
(a) perpendicular
(b) not equal
(c) equal
(d) parallel
 View Answer
View Answer 
Ans: (c)
- According to the transitive property in mathematics, if two things are equal to a third thing, they are also equal to each other.
- This means that if A = C and B = C, then A must equal B.
- Thus, the correct answer is that they are equal to one another.
- Options like "perpendicular" and "not equal" do not apply in this context.
Q28: The ratio of two numbers is 7:5. If both numbers are reduced by 3, their new ratio is 3:2. What is the total of both numbers?
(a) 64
(b) 48
(c) 58
(d) 36
 View Answer
View Answer 
Ans: (d)
- Let the two numbers be 7x and 5x based on the ratio 7:5.
- When we decrease both numbers by 3, we have (7x - 3) and (5x - 3).
- The new ratio is given as 3:2, which leads to the equation: (7x - 3)/(5x - 3) = 3/2.
- Cross-multiplying gives us 2(7x - 3) = 3(5x - 3), simplifying to 14x - 6 = 15x - 9.
- Solving for x, we find x = 3. Therefore, the numbers are 21 and 15, and their sum is 36.
Q29: The area of a triangle, two sides of which are 8 cm and 11 cm and the perimeter is 32 cm, is k × 30 cm². Find the value of k.
(a) 8
(b) 6
(c) 7
(d) 9
 View Answer
View Answer 
Ans: (a)
- To find the area of the triangle, we first need to determine the length of the third side. The perimeter is 32 cm, so the third side is 32 - (8 + 11) = 13 cm.
- Now, we can use Heron's formula to calculate the area. The semi-perimeter (s) is (32 / 2) = 16 cm.
- Using Heron's formula: Area = √[s(s-a)(s-b)(s-c)], where a, b, and c are the sides of the triangle. Here, Area = √[16(16-8)(16-11)(16-13)] = √[16 × 8 × 5 × 3] = √(2400) = 20√(6) cm².
- Since the area is given as k × 30 cm², we can set 20√(6) = k × 30. Solving for k gives k = (20√(6) / 30) = 8.
Q30: Given below are the steps for constructing a quadrilateral PQRS, where PQ = 5 cm, QR = 5.5 cm, and RS = 7 cm, ∠PQR = 75° and ∠QRS = 45°. Which of the following steps is incorrect?
(a) Step 1: Draw QR = 5.5 cm.
(b) Step 2: Draw ∠XQR = 75° at Q and ∠QRY = 45° at R.
(c) Step 3: With Q as centre and radius 5 cm, draw an arc to intersect QX at P.
(d) Step 4: With R as centre and radius 7 cm, draw an arc to intersect RY at S. Join P to S. Thus, PQRS is the required quadrilateral.
 View Answer
View Answer 
Ans: (c)
- The incorrect step in constructing quadrilateral PQRS is Step 3.
- In this step, it states to draw an arc from Q with a radius of 5 cm to find point P.
- However, the correct construction should ensure that the angle and lengths are consistent with the given dimensions.
- Thus, the arc may not intersect correctly, leading to an inaccurate quadrilateral.
Q31: ABCD is a parallelogram. If side AB is extended to point E such that line ED bisects side BC at point O, which of the following statements is true?
(a) AB = OE
(b) AB = BE
(c) OE = OC
(d) None of these
 View Answer
View Answer 
Ans: (b)
- In a parallelogram, opposite sides are equal. Here, AB is extended to E.
- Since ED bisects BC at O, it means BO is equal to OC.
- From the properties of the parallelogram, we can conclude that AB is equal to BE because E is just an extension of AB.
- Thus, the correct statement is that AB = BE.
Q32: If 2/3x – 4/5y = 4 and xy = 60, what is the value of 4/9x² + 16/25y²?
(a) 76
(b) 80
(c) 48
(d) 56
 View Answer
View Answer 
Ans: (b)
- We start with the equations 2/3x – 4/5y = 4 and xy = 60.
- From xy = 60, we can express y in terms of x: y = 60/x.
- Substituting this into the first equation allows us to solve for x and then find y.
- After finding x and y, we can calculate 4/9x² + 16/25y² to get the final result, which is 80.
Q33: Two lines are given to be parallel. The equation of one of the lines is 3x – 2y = 5. The equation of the second line can be
(a) 9x + 8y = 7
(b) -12x – 8y = 7
(c) -12x + 8y = 7
(d) 12x + 8y = 7
 View Answer
View Answer 
Ans: (c)
Q34: In the given figure (not to scale), PQ|| BC and AQ: QC = 3 : 2. If PQ = 15 cm, then find the length of BC (in cm).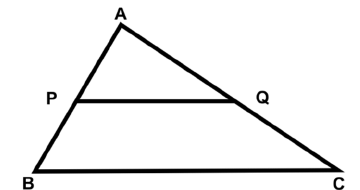 (a) 20 cm
(a) 20 cm
(b) 15 cm
(c) 25 cm
(d) 22 cm
 View Answer
View Answer 
Ans: (c)
We have ∆APQ ~ ∆ABC
So,
Let AQ = 3x, QC = 2x (AQ : QC = 3 :2)
∴ AC = AQ + QC = 5x 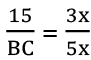
⇒ BC = 25 cm
Q35: A cone, a hemisphere, and a cylinder are constructed with identical bases and heights. What is the ratio of their volumes?
(a) 2 : 1 : 3
(b) 1 : 2 : 3
(c) 3 : 1 : 2
(d) 1 : 3 : 2
 View Answer
View Answer 
Ans: (b)
- The volume of a cone is calculated as (1/3)πr2h.
- The volume of a hemisphere is (2/3)πr3.
- The volume of a cylinder is πr2h.
- When comparing these volumes, we find that the ratio of the volumes of the cone, hemisphere, and cylinder simplifies to 1 : 2 : 3.
Everyday Mathematics
Q36: If a solid sphere with a radius of 12 cm is transformed into 8 smaller spherical balls of equal size, what is the surface area of each small ball?
(a) 45π cm2
(b) 108π cm2
(c) 144π cm2
(d) 124π cm2
 View Answer
View Answer 
Ans: (c)
- First, calculate the volume of the original sphere using the formula: Volume = (4/3)πr3. Here, r = 12 cm.
- Next, find the volume of the original sphere: Volume = (4/3)π(12)3 = 576π cm3.
- Since this volume is divided into 8 smaller spheres, the volume of each small sphere is: 576π cm3 / 8 = 72π cm3.
- Now, use the volume formula for a sphere to find the radius of the small spheres: Volume = (4/3)πr3, leading to r3 = 54. Thus, the radius of each small sphere is 3√6 cm.
- Finally, calculate the surface area of each small sphere using the formula: Surface Area = 4πr2. Plugging in the radius gives Surface Area = 4π(3√6)2 = 144π cm2.
Q37: A shopkeeper marked an article 25% higher than its cost price (C.P.) and then offered a discount of 10% on that marked price. What is the profit percentage for the shopkeeper on that article?
(a) 15 3/4%
(b) 8 1/3%
(c) 9 4/5%
(d) 12 1/2%
 View Answer
View Answer 
Ans: (d)
- Let the cost price (C.P.) of the article be 100.
- The marked price (M.P.) is then 125 (which is 25% above C.P.).
- After applying a 10% discount, the selling price (S.P.) becomes 112.5 (which is 90% of M.P.).
- The profit is calculated as S.P. - C.P. = 112.5 - 100 = 12.5.
- The profit percentage is then (Profit/C.P.) * 100 = (12.5/100) * 100 = 12.5%.
Q38: A triangular park has sides measuring 120 m, 80 m, and 50 m. A gardener needs to plant grass inside. What is the area available for planting?
(a) 180√5 m2
(b) 375√15 m2
(c) 270√5 m2
(d) 225√15 m2
 View Answer
View Answer 
Ans: (b)
- To find the area of a triangle with sides 120 m, 80 m, and 50 m, we can use Heron's formula.
- First, calculate the semi-perimeter (s): s = (120 + 80 + 50) / 2 = 125 m.
- Then, apply Heron's formula: Area = √[s(s-a)(s-b)(s-c)], where a, b, and c are the sides of the triangle.
- Substituting the values gives us the area as 375√15 m², which is the area available for planting.
Q39: In a hostel with 300 students, there is enough food to last for 24 days. After some students departed, the food now lasts for 36 days. How many students have departed from the hostel?
(a) 175
(b) 150
(c) 200
(d) 100
 View Answer
View Answer 
Ans: (d)
- The total amount of food can be calculated as 300 students * 24 days = 7200 student-days of food.
- After some students left, the food lasts for 36 days. Let the number of remaining students be x.
- Now, the food can also be expressed as x students * 36 days = 7200 student-days of food.
- Setting the equations equal gives us 7200 = x * 36, leading to x = 200 students remaining.
- Thus, the number of students who left is 300 - 200 = 100.
Q40: The price of a notebook is double that of a pen. If the notebook costs ₹x and the pen costs ₹y, which linear equation in two variables represents this situation?
(a) x + 2y = 0
(b) x – 2y = 0
(c) 2x + y = 0
(d) 2x – y = 0
 View Answer
View Answer 
Ans: (b)
- The problem states that the cost of a notebook is twice the cost of a pen.
- This means if the pen costs ₹y, then the notebook costs ₹2y.
- We can express this relationship as x = 2y, which can be rearranged to x - 2y = 0.
- Thus, the correct equation that represents this condition is x – 2y = 0.
Q41: A, B, and C are three taps connected to a tank. A and B together fill the tank in 8 hours, B and C together fill it in 12 hours, while A and C together fill the tank in 16 hours. In how much time will A, B, and C together fill up the tank?
(a) 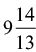 hours
hours
(b) 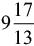 hours
hours
(c) 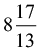 hours
hours
(d) 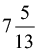 hours
hours
 View Answer
View Answer 
Ans: (d)
- To find the time taken by A, B, and C together, we first calculate their individual rates of filling the tank.
- A and B together fill the tank in 8 hours, so their combined rate is 1/8 of the tank per hour.
- B and C together fill it in 12 hours, giving a rate of 1/12 of the tank per hour.
- A and C together fill it in 16 hours, resulting in a rate of 1/16 of the tank per hour.
- By adding these rates and solving for the combined rate of A, B, and C, we find that they can fill the tank together in
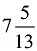 hours.
hours.
Q42: By walking at 5/7 of his normal speed, a man arrives at his office 14 minutes later than he usually does. What is the time he typically takes to reach his office?
(a) 35 mins
(b) 49 mins
(c) 63 mins
(d) 1 hr 12 mins
 View Answer
View Answer 
Ans: (a)
- The man walks at 5/7 of his usual speed, which means he is slower than normal.
- This slower speed causes him to be 14 minutes late.
- To find his usual time, we can set up a relationship between speed, time, and distance.
- Since speed and time are inversely related, if speed decreases, time increases. Thus, we can calculate that his usual time is 35 minutes.
Q43: At a gathering, a specific number of individuals attended. Every attendee donated twice the amount of rupees as the total count of attendees. Given that the overall contribution was ₹4418, determine how many individuals were at the gathering.
(a) 36
(b) 38
(c) 41
(d) 47
 View Answer
View Answer 
Ans: (d)
- Let the number of people be represented as x.
- Each person contributed 2x rupees.
- The total contribution can be expressed as x * 2x = 2x2.
- Setting this equal to the total contribution, we have 2x2 = 4418.
- Solving for x, we find x2 = 2209, leading to x = 47.
Q44: 8 children and 12 men finish a specific task in 9 days. If each child requires double the time a man needs to complete the work, how many days will it take for 12 men to complete the same task?
(a) 8 days
(b) 15 days
(c) 9 days
(d) 12 days
 View Answer
View Answer 
Ans: (d)
- To solve this, we first determine the work done by men and children. If a man completes the work in 1 day, then a child takes 2 days.
- In 1 day, 12 men can do 12 units of work, while 8 children can do 4 units (since 8 children do 4 units in 1 day).
- Thus, together they complete 16 units of work in 1 day.
- Over 9 days, they finish 144 units of work (16 units/day * 9 days).
- Now, if only 12 men work, they can complete 12 units of work per day, so to finish 144 units, it will take them 12 days (144 units / 12 units/day).
Q45: A rectangular field has an area of (14x2 – 11x – 15) m2. What could be the possible expressions for the length and breadth of the field?
(a) (3x – 2) m and (5x + 8) m
(b) (7x + 5) m and (2x – 3) m
(c) Both A and B
(d) None of these
 View Answer
View Answer 
Ans: (b)
- The area of the rectangle is given as (14x2 – 11x – 15) m2.
- To find the length and breadth, we need to factor this expression.
- Factoring gives us (7x + 5) and (2x – 3), which are valid dimensions.
- Option (a) does not yield the correct area when multiplied, confirming that option (b) is the correct answer.
Achievers Section
Q46: I is the incentre of a right triangle ABC. If AB = BC, then find the measure of ∠AIC.
(a) 125°
(b) 135°
(c) 115°
(d) 105°
 View Answer
View Answer 
Ans: (b)
In ΔABC, AB = BC.
⇒ ∠B=90°
∠AIC = 90° + ∠B/2
= 90° + 45° =135°
Q47: In a Rhombus PRST, the diagonal PS is equal to the side of the rhombus. Find the measure of ∠RST.
(a) 130°
(b) 120°
(c) 180°
(d) 125°
 View Answer
View Answer 
Ans: (b)
PRST is a rhombus. All sides are equal.
= ∠PRS = 60° = ∠RST =120°
Q48: One of the sides of the parallelogram is y cm and the other side is (y + 10) cm. The perimeter of the parallelogram is 180 cm. Find the sides of the parallelogram.
(a) 40 cm and 50 cm
(b) 30 cm and 50 cm
(c) 10 cm and 20 cm
(d) 40 cm and 30 cm
 View Answer
View Answer 
Ans: (a)
The sides are 40 cm and 50 cm.
Q49: In a parallelogram STUV, ∠V = 50°. Find the measure of ∠S.
(a) 115°
(b) 120°
(c) 130°
(d) 105°
 View Answer
View Answer 
Ans: (c)
Opposite angles are supplementary. 180° - 50° = 130°
Q50: If PQ and RS are two perpendicular diameters of a circle, what is PRQS?
(a) A square
(b) A rectangle
(c) A triangle
(d) A trapezium
 View Answer
View Answer 
Ans: (a)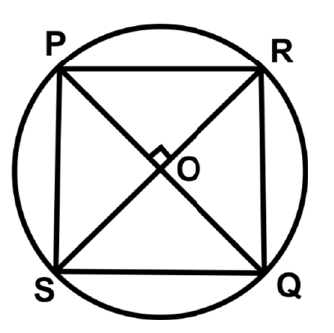
Let the diagonals meet at O as shown in the figure.
∠POS = ∠ROQ = 90°
Also, OP = OQ = OS = OR, i.e., the diagonals are equal and bisect at right angles. Clearly, PRQS is a square.
|
25 videos|117 docs|45 tests
|
FAQs on Maths Olympiad Previous Year Paper -1 - Mathematics Olympiad for Class 9
| 1. What topics are covered in the Class 9 Maths Olympiad Previous Year Paper -1? |  |
| 2. How can I effectively prepare for the Maths Olympiad? |  |
| 3. What is the format of the Maths Olympiad exam for Class 9? |  |
| 4. Where can I find previous year question papers for Class 9 Maths Olympiad? |  |
| 5. What are the benefits of participating in the Maths Olympiad? |  |




















