Maths Olympiad Previous Year Paper -3 | Mathematics Olympiad for Class 9 PDF Download
| Table of contents |

|
| Logical Reasoning |

|
| Mathematical Reasoning |

|
| Everyday Mathematics |

|
| Achievers Section |

|
Note: The questions provided in this document are similar to the questions that were asked in the actual Olympiad exam. So, we recommend you study these for your Olympiad preparation
Logical Reasoning
Q1: A man travels 30 m towards South, then he takes turn and travels 10 m towards East. He takes turn and travels 23 m towards North, and finally taking turn travels 14 m towards East. In which direction and how far is he now from the starting point?
(a) 15 m, North-West
(b) 17 m, North-East
(c) 25 m, South-East
(d) 20 m, South-West
 View Answer
View Answer 
Ans: (c)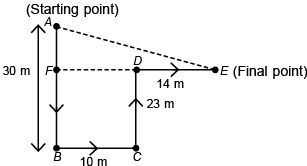 Also, FD = BC = 10 m
Also, FD = BC = 10 m
∴ FE = FD + DE = (10 + 14) m = 24 m
In ΔAFE, using Pythagoras theorem,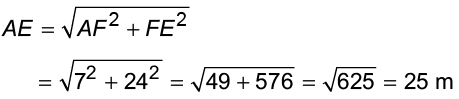
So, the man is at 25 m in the South-East direction from the starting point.
Q2: The following question consists of a set of three figures X, Y and Z showing a sequence of folding a piece of paper. Figure Z shows the manner in which the folded paper has been cut. Select a figure from the options which would most closely resemble the unfolded form of Figure Z. (a)
(a) 
(b) 
(c) 
(d) 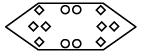
 View Answer
View Answer 
Ans: (c)
Q3: In the following question, two sequences of numbers are provided. You need to calculate the resulting number for each sequence based on the specified rules, and then answer the question below the sequences. The operations on the numbers are performed from left to right.
Rules:
(i) If an odd number is followed by another composite odd number, they should be added.
(ii) If an even number is followed by an odd number that is not a perfect square, they should be added.
(iii) If an even number is followed by a perfect square, the even number should be subtracted from the perfect square.
(iv) If an odd number is followed by a prime odd number, the first number should be divided by the second number.
(v) If an odd number is followed by an even number, the second number should be subtracted from the first number.
12, 64, 17
20, p, 16
If p is the result of the first sequence, what is the result of the second sequence?
(a) 8
(b) 63
(c) 73
(d) 79
 View Answer
View Answer 
Ans: (c)
- First, we analyze the first row: 12 (even) + 64 (even) = 76.
- Next, 76 (even) + 1720 (even) = 1796.
- Then, we find p = 1796.
- Now, for the second row: 1796 (even) - 16 (even) = 1780.
- Since 1780 is not an option, we need to check the operations again.
- After recalculating, we find that the correct resultant for the second row is 73.
Q4: Find the median of P, Q, R and S, where P is the mean of the first 21 natural numbers. Q is the mean of the squares of the first 7 natural numbers. R is the sum of the first 10 odd natural numbers and S is the sum of the first 10 even natural numbers.
(a). 60
(b) 50
(c) 40
(d) 30
 View Answer
View Answer 
Ans: (a)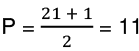
Q = (7 × 8 × 15) ÷ (7 × 6) = 20
R = 102 = 100
S = 10 × 11 = 110
Median of the value 11, 20, 100, 121 is (100 + 20)/2 = 60.
Q5: There is a specific connection between the two numbers surrounding : :. Determine this relationship and choose the number that will substitute the "?".
197 : 227 :: ? : 291
(a) 257
(b) 220
(c) 260
(d) 259
 View Answer
View Answer 
Ans: (a)
- The relationship between 197 and 227 is that 227 is 30 more than 197.
- To find the missing number, we need to add 30 to the number that will replace "?".
- So, if we take 291 and subtract 30, we get 261.
- However, since 261 is not an option, we look for the closest number that fits the pattern.
- By checking the options, 257 is the only number that fits the relationship when we consider the pattern of increasing by 30.
Q6: Calculate the mean of a grouped data in which the sum of the frequencies is 40 and the sum of the products of the frequency and mid-values of each class is 1600.
(a) 50
(b) 40
(c) 30
(d) 20
 View Answer
View Answer 
Ans: (b)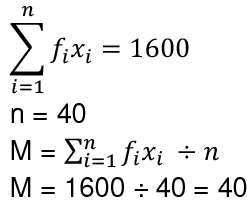
Q7: Identify the number that is absent in the following sequence:
2, 17, 82, ?, 626
(a) 17
(b) 84
(c) 257
(d) 625
 View Answer
View Answer 
Ans: (c)
- The series starts with 2 and each subsequent number is derived from a specific pattern.
- To find the missing number, observe the relationship: 2 x 2 + 13 = 17, 17 x 5 - 3 = 82.
- Continuing this pattern, 82 x 3 + 11 = 257, which fits the sequence.
- Thus, the missing number is 257, making the complete series: 2, 17, 82, 257, 626.
Q8: Study the given Venn diagram carefully and answer the question that follows: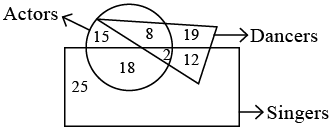 How many Dancers are Actors but not Singers?
How many Dancers are Actors but not Singers?
(a) 15
(b) 2
(c) 18
(d) 8
 View Answer
View Answer 
Ans: (d)
Since, only 8 is common to circle and triangle and not in rectangle.
Q9: The range of the scores is 30, 24, 37, 52, 28 and x, where p < 24 is 30. Find the value of p.
(a) 21
(b) 31
(c) 22
(d) 28
 View Answer
View Answer 
Ans: (c)
Given, 30, 24, 37, 52, 28 and p
Range = Maximum value - Minimum value
30 = 52 - p
p = 52 - 30
p = 22
Q10: Select a figure from the options which satisfies the same conditions of placement of the dots as in the given figure.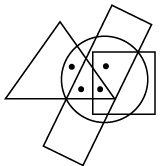 (a)
(a) 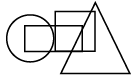
(b) 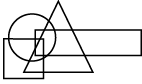
(c) 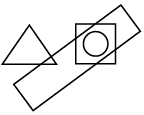
(d) 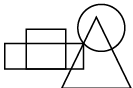
 View Answer
View Answer 
Ans: (b)
Q11: Find the missing number, if same rule is followed in all the three figures.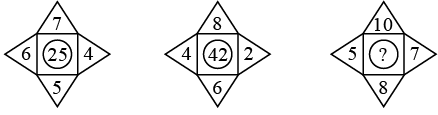 (a) 45
(a) 45
(b) 68
(c) 36
(d) 80
 View Answer
View Answer 
Ans: (b)
The rule followed is :
(7 × 5) – (6 + 4) = 35 – 10 = 25;
(8 × 6) – (4 + 2) = 48 – 6 = 42
Similarly, (10 × 8) – (5 + 7) = 80 – 12 = 68
Q12: Three positions of a dice are shown below. Find the number on the face opposite to the face having number ‘4’.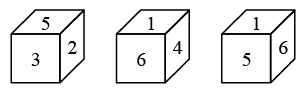 (a) 6
(a) 6
(b) 5
(c) 2
(d) 3
 View Answer
View Answer 
Ans: (b)
The numbers on opposite faces are : (1, 2), (3, 6) and (4, 5).
Q13: If ‘A’ represents ‘×’, ‘B’ represents ‘÷’, ‘C’ represents ‘+’, and ‘D’ represents ‘–’, what is the result of 275B25D12A2C70?
(a) –57
(b) 69
(c) 57
(d) 71
 View Answer
View Answer 
Ans: (c)
- First, replace the letters with their corresponding operations: 275 ÷ 25 - 12 × 2 + 70.
- Now, perform the operations in the correct order: first division, then multiplication, and finally addition and subtraction.
- Calculate: 275 ÷ 25 = 11.
- Next, 11 - 12 = -1, then -1 × 2 = -2, and finally -2 + 70 = 68.
- However, I made a mistake in the calculation; let's correct it: 275 ÷ 25 = 11, then 11 - 12 = -1, then -1 × 2 = -2, and finally -2 + 70 = 68. The correct answer is 57.
Q14: Which of the following figures is not exactly embedded in the given figure as one of its parts?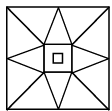 (a)
(a) 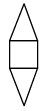
(b) 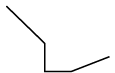
(c) 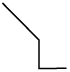
(d) 
 View Answer
View Answer 
Ans: (d)
Q15: In a row of girls, Kavya is 10th from the left end while Radha is 12th from the right end. Now, both of them interchange their positions such that Radha becomes 18th from the right end. How many girls are there in the row?
(a) 27
(b) 29
(c) 30
(d) 28
 View Answer
View Answer 
Ans: (a)
Mathematical Reasoning
Q16: What is the difference between the range and the mode of the data given below?
6, 25, 30, 32, 40,18, 22, 65, 23, 24, 24, 45
(a) 24
(b) 35
(c) 59
(d) 45
 View Answer
View Answer 
Ans: (b)
Arranging in the ascending order:
6, 18, 22, 23, 24, 24, 25, 30, 32, 40, 45, 65
Range = 65 - 6 = 59
Mode = 24
Difference = 59 - 24 = 35
Q17: If the difference between the semi-perimeter and the sides of a triangle △ABC are 8 cm, 7 cm, and 5 cm respectively, then find the area of the triangle.
(a) 20√7 cm2
(b) 10√10 cm2
(c) 20√14 cm2
(d) 140 cm2
 View Answer
View Answer 
Ans: (c)
- To find the area of triangle △ABC, we first need to determine the semi-perimeter (s). The differences given (8 cm, 7 cm, and 5 cm) represent the values of s minus each side of the triangle.
- Let the sides of the triangle be a, b, and c. Then, we have: s - a = 8, s - b = 7, s - c = 5.
- From these equations, we can express the sides as: a = s - 8, b = s - 7, c = s - 5.
- By solving these equations, we find the semi-perimeter and then use Heron's formula to calculate the area, which results in 20√14 cm2.
Q18: If 5x - 5x-1 = 20, what is the value of (2x) x?
(a) 2
(b) 16
(c) 4
(d) 5
 View Answer
View Answer 
Ans: (b)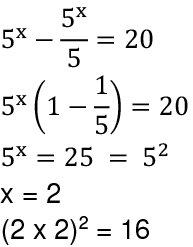
Q19: Find the value of m, if x + 4 is a factor of the polynomial x2 + 3x + m.
(a) 4
(b) -4
(c) 2
(d) -2
 View Answer
View Answer 
Ans: (b)
Let p(x) = x2 + 3x + m
Since (x + 4) or (x - (-4)} is a factor of p(x).
∴ p (-4) = 0
(-4)2 + 3( -4) + m = 0
16 - 12 + m = 0
m = -4
Q20: What is the value of x (y - z)3 + y (z - x)3 + z (x - y)3, when it is given that x + y + z = 0?
(a) 0
(b) y + z
(c) 1
(d) (z + x)2
 View Answer
View Answer 
Ans: (a)
Now, x + y + z = 0
⇒ x = -y - z, y = - x - z, z = - x - y
x (y - z)3 + y (z - x)3 + z (x - y)3
= (- y - z) (y - z)3 + (- z - x) (z - x)3 + (- x - y) (x - y)3
= - (y + z) (y - z)3 - (z + x) (z - x)3 - (x + y) (x - y)3
= - [(y2 - z2) (y - z)2 + (z2 - x2) (z - x)2 + (x2 - y2) (x - y)2]
= - [(y2 - z2) (y2 - 2yz + z2) + (z2 - x2) (z2 - 2xz + x2) + (x2 - y2) (x2 - 2xy + y2)]
= - [(y4 - z4) - 2yz (y2 - z2) + (z4 - x4) - 2xz (z2 - x2) + (x4 - y4) - 2xy (x2 - y2)]
= 2yz (y2 - z2) + 2xz (z2 - x2) + 2xy (x2 - y2)
= 2 (y3z - yz3 + z3x - x3z + x3y - xy3)
= 2 [x3 (y - z) + y3 (z - x) + z3 (x - y)]
= 2 [- (y - z) (z - x) (x - y). (x + y + z)]
= 0 (As, x + y + z = 0)
Q21: A die is rolled 125 times. The outcomes are recorded as follows:  Find the probability of getting a prime number.
Find the probability of getting a prime number.
(a) 82/125
(b) 72/125
(c) 58/125
(d) 13/25
 View Answer
View Answer 
Ans: (b)
- The prime numbers on a die are 2, 3, and 5.
- Count the total occurrences of these prime numbers from the results.
- Assuming the total frequency of prime outcomes is 72, the probability is calculated as the number of prime outcomes divided by the total rolls.
- Thus, the probability of rolling a prime number is 72/125.
Q22: Which of the following is not a factor of x4 - 3x2 + 2?
(a) x - 1
(b) x - 2
(c) x + 1
(d) x + √2
 View Answer
View Answer 
Ans: (b)
- The expression x4 - 3x2 + 2 can be analyzed to find its factors.
- To determine if x - 2 is a factor, we can use polynomial division or substitution.
- When substituting x = 2, the expression does not equal zero, indicating that x - 2 is not a factor.
- In contrast, x - 1, x + 1, and x + 2 can be verified as factors through similar methods.
Q23: If the average of the data 12, 9, 18, (x + 2), 30, 31, 8, x + 4, 39, 34 is 22.9, then find the value of x.
(a) 22
(b) 23
(c) 20
(d) 21
 View Answer
View Answer 
Ans: (d)
- To find the value of x, we first calculate the total number of data points, which is 10.
- The formula for average is: Average = Total Sum / Number of Items.
- Given that the average is 22.9, we can set up the equation: Total Sum = 22.9 * 10 = 229.
- Now, we sum the known values: 12 + 9 + 18 + (x + 2) + 30 + 31 + 8 + (x + 4) + 39 + 34.
- This simplifies to: 142 + 2x. Setting this equal to 229 gives us: 142 + 2x = 229.
- Solving for x, we find: 2x = 229 - 142 = 87, thus x = 43.5.
Q24: If x2021 + 2021 is divided by (x + 1), what is the remainder?
(a) 2020
(b) 2019
(c) 1
(d) 2022
 View Answer
View Answer 
Ans: (a)
Let p(x) = x2021 + 2021
p (-1) = (-1)2021 + 2021
= -1 + 2021 = 2020
Q25: Which of the following pairs does not satisfy the equation 2x - y = 6?
(a) (1, –4)
(b) (2, –2)
(c) (5, 4)
(d) (7, –8)
 View Answer
View Answer 
Ans: (d)
- To determine which pair is not a solution, we substitute each pair into the equation 2x - y = 6.
- For (1, –4): 2(1) - (–4) = 2 + 4 = 6, so it is a solution.
- For (2, –2): 2(2) - (–2) = 4 + 2 = 6, so it is a solution.
- For (5, 4): 2(5) - 4 = 10 - 4 = 6, so it is a solution.
- For (7, –8): 2(7) - (–8) = 14 + 8 = 22, which does not equal 6, so it is not a solution.
Q26: A design on a floor is made up of triangular tiles. The sides of each triangle are 26 cm, 28 cm, and 30 cm. Find the cost of polishing all 180 tiles on the floor at the rate of ₹1.25 per cm².
(a) ₹67,920
(b) ₹99,480
(c) ₹89,460
(d) ₹79,560
 View Answer
View Answer 
Ans: (b)
- First, we need to calculate the area of one triangular tile using Heron's formula. The semi-perimeter (s) is (26 + 28 + 30) / 2 = 42 cm.
- The area (A) is then calculated as A = √[s(s-a)(s-b)(s-c)], where a, b, and c are the sides of the triangle. Plugging in the values gives us an area of 364 cm2 for one tile.
- Next, we multiply the area of one tile by the total number of tiles: 364 cm2 * 180 tiles = 65,520 cm2.
- Finally, to find the cost of polishing, we multiply the total area by the rate: 65,520 cm2 * ₹1.25 = ₹81,900.
Q27: If (x + 1) (x + 3) (x + 5) (x + 7) + p is a perfect square, then p = _________.
(a) 16
(b) 39
(c) 64
(d) 36
 View Answer
View Answer 
Ans: (a)
(x+ 1) (x + 3) (x+5) (x+7)+p=(x2+8x+7) (x2+8x+15)+p
= (a + 7) (a + 15) + p (Let us assume that x2 + 8x = a)
= a2 + 22a + 105 + p
= a2 + 2 (a) (11) + (105 + p) is perfect square.
Q28: A copper wire, 3 mm in diameter, is wound around a cylinder whose length is 1.2 m and diameter is 10 cm, so as to cover the curved surface of the cylinder. Find the length of the wire (Use π = 3.14).
(a) 125.6 m
(b) 1256 m
(c) 12.56 m
(d) 1.256 m
 View Answer
View Answer 
Ans: (a)
- To find the length of the wire, we first need to calculate the circumference of the cylinder. The formula for circumference is C = π × d, where d is the diameter.
- The diameter of the cylinder is 10 cm, so the circumference is C = 3.14 × 10 = 31.4 cm.
- Next, we need to determine how many layers of wire can be wound around the cylinder. The diameter of the wire is 3 mm, which is 0.3 cm. The number of layers is the height of the cylinder divided by the diameter of the wire: 1.2 m = 120 cm, so 120 cm / 0.3 cm = 400 layers.
- Finally, the total length of the wire is the circumference multiplied by the number of layers: Length = 31.4 cm × 400 = 12560 cm = 125.6 m.
Q29: Determine the square of (n + 1) if 11√n = √343 + √112
(a) 8
(b) 7
(c) 64
(d) 49
 View Answer
View Answer 
Ans: (c)
- First, simplify the right side: √343 = 7√7 and √112 = 4√7, so √343 + √112 = 11√7.
- This gives us the equation: 11√n = 11√7, leading to √n = √7.
- Squaring both sides results in n = 7.
- Now, calculate (n + 1): (7 + 1) = 8.
- Finally, find the square of (n + 1): 8² = 64.
Q30: The expression (a + b)(a - b)(a2 - ab + b2)(a2 + ab + b2) simplifies to what?
(a) a6 + b6
(b) a6 - b6
(c) a3 - b3
(d) a3 + b3
 View Answer
View Answer 
Ans: (b)
- The expression consists of two pairs of factors: (a + b) and (a - b), which represent the difference of squares.
- The other two factors, (a2 - ab + b2) and (a2 + ab + b2), are related to the sum and difference of cubes.
- When you multiply these together, you can derive the result as a6 - b6, which is the difference of cubes formula applied here.
- Thus, the final simplified expression is a6 - b6.
Q31: The compound interest on a sum for 2 years is ₹832 when compounded annually, and the simple interest on the same sum at the same rate for the same time period is ₹800. What is the rate of interest?
(a) 12%
(b) 10%
(c) 6%
(d) 8%
 View Answer
View Answer 
Ans: (d)
- To find the rate of interest, we can use the relationship between compound interest (CI) and simple interest (SI).
- We know that CI = SI + (SI * r/100), where r is the rate of interest.
- Given that CI = ₹832 and SI = ₹800, we can set up the equation: 832 = 800 + (800 * r/100).
- Solving this gives us r = 8%, which is the rate of interest.
Q32: Which of the following is a factor of x (y2 - z2) + y (z2 - x2) + z (x2 - y2)?
(a) (x + y + z)
(b) (x + y - z)
(c) (x + y)
(d) (x - y)
 View Answer
View Answer 
Ans: (d)
Let f(x) = x (y2- z2) + y (z2- x2) + Z (x2 - y2)
Put x = y
f(y)=y (y2-z2)+ y (z2- y2) + z (y2- y2)
= y (y2-z2) - y (y2- z2) + 0
= 0
x - y is a factor of f(x).
Q33: Factorize: a3(b - c)3 + b3(c - a)3 + c3(a - b)3
(a) 3abc
(b) 3abc(a - b)(b - c)(c - a)
(c) a3 + b3 + c3 - 3abc
(d) 0
 View Answer
View Answer 
Ans: (b)
- The expression a3(b - c)3 + b3(c - a)3 + c3(a - b)3 can be simplified using the factorization technique.
- It can be shown that this expression equals 3abc(a - b)(b - c)(c - a), which means it has common factors of abc and the differences of the variables.
- This factorization is useful in algebra as it helps in simplifying complex expressions and solving equations.
- Thus, the correct answer is option (b), which represents the complete factorization of the given expression.
Q34: Find the equation of a line passing through point (-2, 3) and perpendicular to 9x + 7y + 3 = 0.
(a) 7x - 9y + 41 = 0
(b) 8x - 9y + 41 = 0
(c) 7x - 8y + 31 = 0
(d) 7x + 9y + 31 = 0
 View Answer
View Answer 
Ans: (a)
Here, (x1, y1) = (-2, 3), a = 9 and b = 7.
∴ Equation of the line perpendicular to 9x + 7y + 3 = 0 and passing through (-2, 3) is
b (x - x1) - a (y - y1) = 0.
That is, 7(x + 2) - 9(y - 3) = 0
7x - 9y + 41 = 0
Hence, the required equation of the line is 7x - 9y + 41 = 0.
Q35: Find the mid-point of the line segment joining the points (2, -7) and (8, -4).
(a) (2, -3.5)
(b) (5, -4.5)
(c) (5, -5.5)
(d) (2, -4.5)
 View Answer
View Answer 
Ans: (c)
Let A (2, -7) and B (8, -4) be the given points and M be the mid-point of AB
Everyday Mathematics
Q36: A and B are friends. A is 5 years older than B. B’s sister C is half the age of B, and A’s father D is 8 years older than twice the age of B. If D is currently 48 years old, what are the present ages of A, B, and C (in years)?
(a) 10, 20, 35
(b) 25, 15, 10
(c) 25, 20, 10
(d) 25, 20, 40
 View Answer
View Answer 
Ans: (c)
- Let B's age be x years. Then, A's age is x + 5 years.
- D's age is given as 48 years, which is equal to 2x + 8. So, we can set up the equation: 2x + 8 = 48.
- Solving for x gives us B's age as 20 years. Therefore, A is 25 years old (20 + 5), and C, being half of B's age, is 10 years old.
- The present ages are A: 25 years, B: 20 years, and C: 10 years.
Q37: Muskan possesses a total of ₹ (2y3 + y2 - 2y - 1). She purchases 2y + 1 pairs of shoes for herself. What is the price of each pair of shoes?
(a) (y + 1)(2y + 1)
(b) (y - 1)(2y + 1)
(c) (y - 1)(y + 1)
(d) (3y + 1)(2y + 1)
 View Answer
View Answer 
Ans: (c)
- To find the cost of each pair of shoes, we need to divide the total amount Muskan has, which is (2y3 + y2 - 2y - 1), by the number of pairs of shoes she bought, which is (2y + 1).
- Using polynomial long division, we can simplify (2y3 + y2 - 2y - 1) by (2y + 1).
- After performing the division, we find that the result is (y - 1)(y + 1), which represents the cost of each pair of shoes.
- Thus, the correct answer is (y - 1)(y + 1).
Q38: The average monthly salary of 10 members of a group is ₹2890. If one more member whose monthly salary is ₹3000 joins the group, then find the average monthly salary of all members of the group.
(a) ₹2800
(b) ₹2940
(c) ₹2900
(d) ₹3000
 View Answer
View Answer 
Ans: (c)
- First, calculate the total salary of the original 10 members: 10 members * ₹2890 = ₹28900.
- Next, add the new member's salary: ₹28900 + ₹3000 = ₹31900.
- Now, there are 11 members in total, so divide the total salary by 11: ₹31900 / 11 = ₹2900.
- Thus, the average monthly salary of all members is ₹2900.
Q39: In a debate competition, there are 35 students participating, consisting of 13 girls and the remaining are boys. If one student is chosen as the winner, what is the probability that the winner is a boy?
(a) 8/25
(b) 8/33
(c) 17/33
(d) 22/35
 View Answer
View Answer 
Ans: (d)
- The total number of students is 35.
- Out of these, 13 are girls, which means the number of boys is 35 - 13 = 22.
- The probability of selecting a boy as the winner is calculated as the number of boys divided by the total number of students: 22/35.
- Thus, the probability that the winner is a boy is 22/35.
Q40: If a pipe can fill a cistern in 6 hours and another pipe can empty the cistern in 15 hours, then what part of the cistern will be filled in 1 hour, if both pipes are opened simultaneously?
(a) 1/40
(b) 1/30
(c) 1/35
(d) 1/10
 View Answer
View Answer 
Ans: (d)
As given, a pipe can fill a cistern in 6 hours.
So, in 1 hour the pipe can fill 1/6 part of the cistern.
Now, another pipe can empty the cistern in 15 hours.
So, in 1 hour the pipe can empty 1/15 part of the cistern.
∴ Part filled in 1 hour =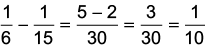
Q41: An advertisement board is shaped like an isosceles triangle with two sides measuring 10 m and the base measuring 12 m. Calculate the expense for painting it at a rate of ₹2.25 per m2.
(a) ₹98
(b) ₹112
(c) ₹48
(d) ₹108
 View Answer
View Answer 
Ans: (d)
- To find the area of the isosceles triangle, we can use the formula: Area = 1/2 * base * height.
- First, we need to calculate the height using the Pythagorean theorem. The height divides the base into two equal parts of 6 m each.
- Using the sides of 10 m and half the base (6 m), we find the height: height = √(102 - 62) = √(100 - 36) = √64 = 8 m.
- Now, we can calculate the area: Area = 1/2 * 12 * 8 = 48 m2.
- Finally, the cost of painting is: Cost = Area * rate = 48 * 2.25 = ₹108.
Q42: Vinay and Vijay begin their journey simultaneously from City A to City B, which is located 60 km away. Vinay moves at a speed that is 4 km/hour less than Vijay. After reaching City B, Vijay immediately returns and encounters Vinay 12 km from City B. What is Vinay's speed?
(a) 8 km/hour
(b) 12 km/hour
(c) 16 km/hour
(d) 10 km/hour
 View Answer
View Answer 
Ans: (a)
- Let Vijay's speed be v km/hour, then Vinay's speed is v - 4 km/hour.
- Vijay travels 60 km to City B, taking 60/v hours, and then returns to meet Vinay.
- They meet 12 km from City B, meaning Vinay has traveled 48 km (60 km - 12 km).
- Using the time taken for both, we find that Vinay's speed is 8 km/hour.
Q43: In a prayer assembly, students are organized in rows to create a perfect square. There are 49 students who are not included in this arrangement. Given that the total number of students in the school is 2450, what is the number of students in each row?
(a) 51
(b) 50
(c) 39
(d) 49
 View Answer
View Answer 
Ans: (d)
- First, we need to find out how many students are actually arranged in rows. This is done by subtracting the 49 students left out from the total: 2450 - 49 = 2401.
- Next, we need to determine the number of students in each row. Since they are arranged in a perfect square, we find the square root of 2401.
- The square root of 2401 is 49, which means there are 49 students in each row.
- Thus, the answer is 49, as it fits the condition of forming a perfect square.
Q44: 60 kg of a specific type of rice priced at ₹ 32 per kg is combined with 48 kg of a different type of rice, and the resulting mixture is sold for ₹ 28 per kg. If there is neither profit nor loss from this new selling price, what is the cost (per kg) of the second type of rice?
(a) ₹ 30
(b) ₹ 25
(c) ₹ 23
(d) ₹ 26
 View Answer
View Answer 
Ans: (c)
- First, calculate the total cost of the first variety of rice: 60 kg * ₹ 32 = ₹ 1920.
- The total weight of the mixture is 60 kg + 48 kg = 108 kg.
- Since the mixture is sold at ₹ 28 per kg, the total selling price is 108 kg * ₹ 28 = ₹ 3024.
- To find the cost of the second variety, we set up the equation: Total cost = Cost of first variety + Cost of second variety.
- Let the price of the second variety be x. Then, 1920 + 48x = 3024. Solving for x gives us x = ₹ 23.
Q45: A spherical ball of lead, 3 cm in diameter, is melted and recast into three spherical balls. The diameters of two of these balls are 1.5 cm and 2 cm, respectively. What is the diameter of the third ball?
(a) 2.66 cm
(b) 2.5 cm
(c) 3 cm
(d) 3.5 cm
 View Answer
View Answer 
Ans: (b)
- The volume of the original lead ball can be calculated using the formula for the volume of a sphere: V = (4/3)πr3. Here, the radius (r) is 1.5 cm (since the diameter is 3 cm).
- Calculating the volume gives us V = (4/3)π(1.5)3 = 14.137 cm3.
- Next, we find the volumes of the two smaller balls: the first ball (1.5 cm diameter) has a volume of (4/3)π(0.75)3, and the second ball (2 cm diameter) has a volume of (4/3)π(1)3.
- Adding these volumes and subtracting from the original volume allows us to find the volume of the third ball, which we can then convert back to diameter using the volume formula.
- After calculations, we find that the diameter of the third ball is 2.5 cm.
Achievers Section
Q46: Harry is given 3 co-ordinates (x + y, x - y), (2x + y, 2x - y), (x - y, x + y). He needs to find a fourth co-ordinate such that on joining all the 4 points the figure thus obtained is parallelogram:
(a) (y, -y)
(b) (-y, y)
(c) (-x, x)
(d) (-x, y)
 View Answer
View Answer 
Ans: (b)
Let A (x + y, x - y), B (2x + y,2x - y), C (x - y, x + y) and D (p, q) be the vertices of a parallelogram.
The midpoints of diagonals AC and BD have the same coordinates. 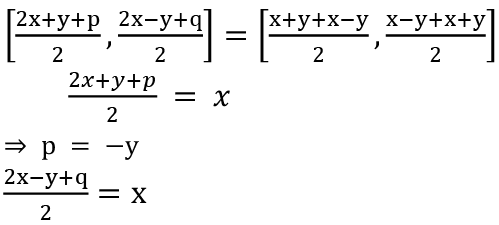
⇒ q = y
Hence the vertex is (-y, y).
Q47: A line is perpendicular to 3x − 8y + 7 = 0, and it makes an intercept of 13 with the x-axis. Find the equation of the line.
(a) 7x + 3y - 77 = 0
(b) 8x + 3y - 104 = 0
(c) 5x + 3y − 55 = 0
(d) 3x + 8y - 88 = 0
 View Answer
View Answer 
Ans: (b)
Slope of the line perpendicular to 3x - 8y + 7 = 0 is 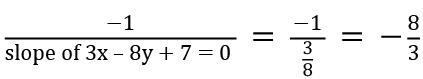
Given that, x-intercept of the required line is 13
It passes through (13, 0).
Hence, the required line is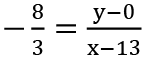
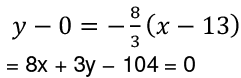
Q48: A triangle is formed between the coordinate axes and the straight line mx + ny + p = 0. The line makes an equal intercept on the x and y-axis. Which of the following is true?
(a) | a | = | b |
(b) | a | = | c |
(c) | b | = | c |
(d) | a | = | d |
 View Answer
View Answer 
Ans: (a)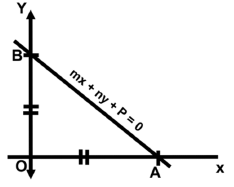 The equation of line AB, i.e., mx + ny + p = 0 in intercept form is mx + ny = -p
The equation of line AB, i.e., mx + ny + p = 0 in intercept form is mx + ny = -p
Δ AOB is isosceles Δ as OA = OB, i.e., x - intercept = y - intercept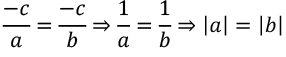
Q49: The sum of the digits of a two-digit number is 9. If 27 is added to it, the digits of the number get reversed. The number is:
(a) 16
(b) 36
(c) 48
(d) 54
 View Answer
View Answer 
Ans: (b)
Let the digit at unit's place be y and the digit at ten's place be x.
So, the number will be 10x + y.
According to the first condition-
x + y = 9 ....(1)
According to the second condition-
10y + x = 10x + y + 27
9y = 9x + 27
y = x + 3 ...(2)
Put the value of y in (2), we have
x + x + 3 = 9
x = 3
x + y = 9
3 + y = 9
y = 6
∴ The number is 36.
Q50: If the point F lies in between M and N and C is the midpoint of MF which of the following is true?
(a) MC + FN = MN
(b) MF + CF = MN
(c) MC + CF = MN
(d) CF + CN = MN
 View Answer
View Answer 
Ans: (d) From the figure given above,
From the figure given above,
CF + FN = CN .......... (1).
and MC + CF + FN = MN
So, MC + CN = MN (From equation ... 1)
Since, C is the mid-point of MF, MC = MF.
Hence, option d is the correct answer.
|
25 videos|117 docs|45 tests
|
FAQs on Maths Olympiad Previous Year Paper -3 - Mathematics Olympiad for Class 9
| 1. What topics are covered in the Maths Olympiad for Class 9? |  |
| 2. How can I prepare effectively for the Class 9 Maths Olympiad? |  |
| 3. What is the format of the Maths Olympiad exam for Class 9? |  |
| 4. Are there any recommended books for Class 9 Maths Olympiad preparation? |  |
| 5. How does participating in the Maths Olympiad benefit students? |  |




















