Maths Olympiad Model Test Paper -1 | Mathematics Olympiad for Class 9 PDF Download
| Table of contents |

|
| Logical Reasoning |

|
| Mathematical Reasoning |

|
| Everyday Mathematics |

|
| Achievers Section |

|
Note: The questions provided in this document are similar to the questions that were asked in the actual Olympiad exam. So, we recommend you study these for your Olympiad preparation
Logical Reasoning
Q1: Which of the following Venn diagrams best represents the relationship amongst, 'Indian Navy, Indian Army, Indian Air Force?
(a) 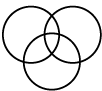
(b) 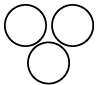
(c) 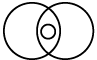
(d) 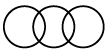
 View Answer
View Answer 
Ans: (b)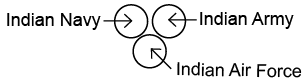
Q2: If 'P' represents 'multiplication', 'Q' represents 'division', 'R' represents 'addition', and 'S' represents 'subtraction', what is the result of 152Q19P10R7S31?
(a) 73
(b) 45
(c) 39
(d) 56
 View Answer
View Answer 
Ans: (d)
- First, replace the letters with their operations: 152Q19 becomes 152 ÷ 19.
- Next, calculate: 152 ÷ 19 = 8.
- Then, replace 'P' with multiplication: 8P10 becomes 8 × 10 = 80.
- Now, replace 'R' with addition: 80R7 becomes 80 + 7 = 87.
- Finally, replace 'S' with subtraction: 87S31 becomes 87 - 31 = 56.
Thus, the final answer is 56.
Q3: In search of fodder four buffaloes and three cows stand in a queue. What is the probability that they will be in alternate positions?
(a) 4/35
(b) 3/35
(c) 2/35
(d) 1/35
 View Answer
View Answer 
Ans: (d)
Total number of ways of arranging 4 buffaloes and 3 cows,
i.e., 7 animals in a queue (row) = n(S) = 7!
Let A: Event in which the 4 buffaloes and 3 cows occupy alternate position.
This is possible when the 4 buffaloes occupy the 4 odd places standing form position 1 and the cows fill in the three even places between
4 buffaloes can be arranged in a queue in 4! ways
3 cows can fill the gaps in the queue in 3! ways.
n(A) = 4! × 3!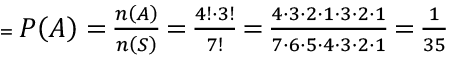
Q4: Pointing to a woman in the picture, Shilpa remarked, "She is the mother of my brother's sole son." What is Shilpa's relationship to the woman in the picture?
(a) Sister
(b) Aunt
(c) Sister-in-law
(d) Mother-in-law
 View Answer
View Answer 
Ans: (c)
- Shilpa mentions that the lady is the mother of her brother's only son.
- This means the lady is the wife of Shilpa's brother, making her Shilpa's sister-in-law.
- Thus, the correct relationship is sister-in-law.
- Other options do not fit the relationship described.
Q5: Find the number of straight lines and triangles in the given figure.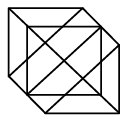 (a) 14 and 18
(a) 14 and 18
(b) 16 and 20
(c) 16 and 24
(d) 14 and 24
 View Answer
View Answer 
Ans: (d)
Number of straight lines = 14
Number of triangles = 24
Q6: Three of the following are alike in a certain way based on the given arrangement and hence form a group. Which one does not belong to the group? 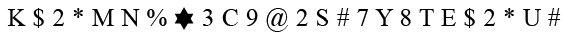 (a) KN97
(a) KN97
(b) *3ST
(c) 
(d) 3S*U
 View Answer
View Answer 
Ans: (d)
Except option D, in all other options, there is a gap of 4 elements between any two consecutive elements.
Q7: Select the correct mirror image of the given figure, if mirror is placed vertically to the right.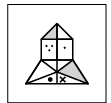 (a)
(a) 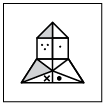
(b) 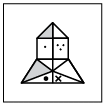
(c) 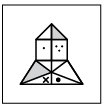
(d) 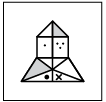
 View Answer
View Answer 
Ans: (c)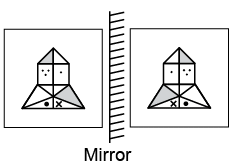
Q8: Himani goes 14 m towards West, then she turns right and walks 10 m, again she turns right and walks 6 m. Then finally she turns left and walks 5 m. How far and in which direction is she now from her starting point?
(a) 17 m, North-West
(b) 11 m, South-East
(c) 17 m, North-East
(d) 11 m, South-West
 View Answer
View Answer 
Ans: (a)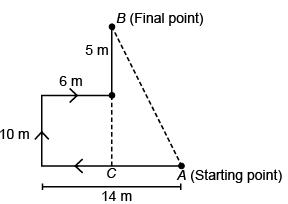
Required distance (AB) 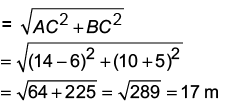
∴ Himani is 17 m in North-West direction from her starting point.
Q9: Group the given figures into three classes on the basis of their identical properties using each figure only once.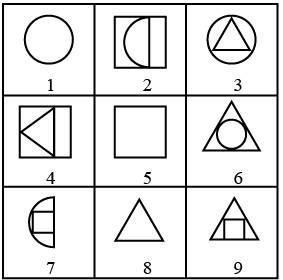 (a) 1, 5, 8; 2, 4, 7; 3, 6, 9
(a) 1, 5, 8; 2, 4, 7; 3, 6, 9
(b) 6, 5, 8; 1, 3, 7; 2, 4, 9
(c) 1, 3, 6; 4, 5, 9; 2, 7, 8
(d) 1, 3, 6; 2, 5, 7; 4, 8, 9
 View Answer
View Answer 
Ans: (a)
1, 5, 8; all are simple 2-D figures.
2, 4, 7; all having two figures, one inside the other.
3, 6, 9; all having two figures, one inside the other.
Q10: If each consonant in the following words is replaced with the letter before it, and each vowel is replaced with the letter after it in the English alphabet, how many of the resulting words contain no vowels?
RAG, FIN, PUT, LOW, SUE
(a) Two
(b) One
(c) Three
(d) More than three
 View Answer
View Answer 
Ans: (a)
- To solve this, we need to change each consonant to the previous letter and each vowel to the next letter.
- For example, in the word "RAG": R becomes Q, A becomes B, and G becomes F, resulting in "QBF".
- Following this process for all words, we find that "FIN" becomes "EHM", "PUT" becomes "OVS", "LOW" becomes "KPV", and "SUE" becomes "RVF".
- After applying the rule, the only words that contain no vowels are RAG (resulting in QBF) and FIN (resulting in EJM).
- Thus, the answer is 2 words.
Q11: Three figures P, Q, R shows a sequence of folding of a sheet of paper. Figure (R) shows the manner in which the folded paper has been cut. Select a figure from the options which represents the unfolded form of figure (R).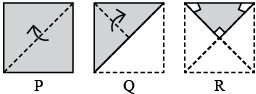 (a)
(a) 
(b) 
(c) 
(d) 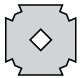
 View Answer
View Answer 
Ans: (d)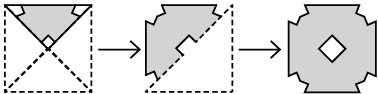
Q12: What will come in place of (?) to continue the given series?
7E19, 11J16, 15O13, 19T10, ?
(a) 22W6
(b) 23Y7
(c) 21U5
(d) 19V6
 View Answer
View Answer 
Ans: (b)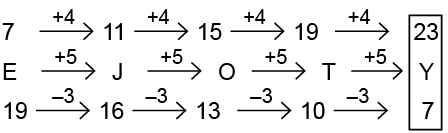
Q13: Select a figure from the options which satisfies the same conditions of placement of the dots as in the given figure.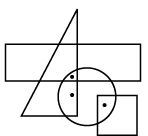 (a)
(a) 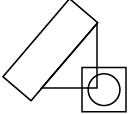
(b) 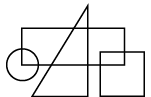
(c) 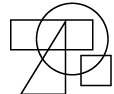
(d) 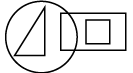
 View Answer
View Answer 
Ans: (c)
Q14: A word arrangement machine takes an input line of words and rearranges them according to specific rules in each step. The following is an example of an input line of words and the steps of rearrangement.
Input: gone are take enough brought station
Step I: take gone are enough brought station
Step II: take are gone enough brought station
Step III: take are station gone enough brought
Step IV: take are station brought gone enough.
Step IV is the final step for this input.
Based on the rules applied in the above steps, answer the following question. If step IV of an input line of words is 'violet for sour height journey medium', which of the following is definitely the input?
(a) violet for journey height sour medium
(b) violet for sour journey height medium
(c) violet journey height for sour medium
(d) can't be determined
 View Answer
View Answer 
Ans: (d)
- The input line of words is rearranged through specific steps.
- In the given example, the final arrangement does not provide enough information to determine the original input.
- Each step changes the order of words, but without knowing the exact rules, we cannot trace back to the original input.
- Thus, the correct answer is that it "can't be determined" from the information provided.
Q15: Find the missing number, if same rule is followed in all three figures. (a) 148
(a) 148
(b) 336
(c) 225
(d) 369
 View Answer
View Answer 
Ans: (d)
The rule followed is:
(92 + 112) = 202;
(62 + 72) = 85
So, (152 + 122) = 369
Mathematical Reasoning
Q16: Ten different slips with the numbers 1 through 10 are kept in a box and thoroughly mixed. Without looking at the slips, one gets picked out of the box. what is the probability of getting number 6
(a) 1/6
(b) 1/10
(c) 9/10
(d) 10/9
 View Answer
View Answer 
Ans: (b)
Sample space = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} → n(S) = 10
Let A be the event of getting 6 from the sample space.
A= {6} → n(A) = 1
Probability of getting number 6 = n(A)/n(S) = 1/10
Q17: From a group of 3 men and 2 women, two people are selected at random. Find the probability that at least one woman is selected:
(a) 1/5
(b) 7/10
(c) 2/5
(d) 5/6
 View Answer
View Answer 
Ans: (b)
To find the probability that at least one woman is selected from the group of 3 men and 2 women, we can proceed as follows:
Total number of ways to select 2 people from 5 (3 men + 2 women):
The total number of ways to select 2 people from 5 is given by the combination formula: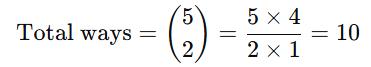
To have at least one woman, we can have:
One woman and one man:
Number of ways to select 1 woman from 2 = C(2, 1) = 2
Number of ways to select 1 man from 3 = C(3, 1) = 3
So, the number of ways to select 1 woman and 1 man = 2 × 3 = 6
Two women:
Number of ways to select 2 women from 2 = C(2, 2) = 1
Thus, the total number of favorable outcomes (at least one woman) is:
6 + 1 = 7
Probability:
The probability of selecting at least one woman is the ratio of favorable outcomes to the total number of outcomes:
Probability = 7 / 10
The correct answer is Option (b) 7/10.
Q18: The dimensions of a cuboidal container are 12 cm x 10 cm x 8 cm. How many bottles of syrup can be poured into the container if each bottle contains 20 cm3 of syrup?
(a) 46
(b) 54
(c) 48
(d) 58
 View Answer
View Answer 
Ans: (c)
Step 1: Find the volume of the cuboidal container.
The volume of a cuboid is given by the formula:
Volume = Length × Width × Height
Substituting the given dimensions:
Volume = 12 cm × 10 cm × 8 cm = 960 cm³
Step 2: Find how many bottles of syrup can be poured into the container.
Each bottle contains 20 cm³ of syrup. To find how many bottles can be poured into the container, we divide the volume of the container by the volume of one bottle:
Number of bottles = Volume of container / Volume of one bottle
Number of bottles = 960 / 20 = 48
Thus, 48 bottles of syrup can be poured into the container.
The correct answer is Option (c) 48.
Q19: A, B and C can complete a piece of work in 25, 30 and 50 days, respectively. They started the work together but A and C left 2 days before the completion of the work. In how many days will the work be completed?
(a) 14
(b) 12
(c) 18
(d) 10
 View Answer
View Answer 
Ans: (b)
Step 1: Find the work rates of A, B, and C.
A's work rate = 1/25 (work per day)
B's work rate = 1/30 (work per day)
C's work rate = 1/50 (work per day)
Step 2: Work done by A, B, and C together in the first (x-2) days.
In the first (x - 2) days, A, B, and C work together. The combined work rate is:
Total work rate = (1/25) + (1/30) + (1/50)
= (6/150) + (5/150) + (3/150)
= (14/150)
= 7/75 (work per day)
So, the work done in the first (x - 2) days is:
Work done = (7/75) × (x - 2)
Step 3: Work done by B in the last 2 days.
After A and C leave, only B continues to work for the last 2 days. B's work rate is 1/30, so the work done by B in the last 2 days is:
Work done by B in 2 days = (1/30) × 2 = 2/30 = 1/15
Step 4: Set up the equation for the total work.
The total work is 1 unit, so the work done by A, B, and C together in the first (x - 2) days plus the work done by B in the last 2 days should add up to 1. The equation is:
(7/75) × (x - 2) + (1/15) = 1
Simplifying the equation:
(7/75) × (x - 2) = 1 - (1/15)
= (15/15) - (1/15)
= 14/15
Now, multiply both sides by 75 to eliminate the denominator:
7(x - 2) = 75 × (14/15)
= 70
Solve for x:
x - 2 = 70 / 7 = 10
x = 10 + 2 = 12
The work will be completed in 12 days.
The correct answer is Option (b) 12.
Q20: In a three-digit number, the digit in the ones place is three times the digit in the hundreds place. The total of the digits in the ones and tens places equals the smallest two-digit number. What is the product of the three digits of the number if all the digits are even
(a) 42
(b) 24
(c) 27
(d) 48
 View Answer
View Answer 
Ans: (d)
- The smallest two-digit number is 10. Since the ones place is three times the hundreds place, the only even digit that fits is 2 (hundreds place) and 6 (ones place).
- The tens place must then be 4 to make the sum of the ones and tens places equal to 10 (6 + 4 = 10).
- The three digits are 2, 4, and 6. The product of these digits is 2 x 4 x 6 = 48.
- Thus, the product of the three digits is 48.
Q21: Which of the following solids has twice the number of edges than faces?
(a) Triangular Prism
(b) Rectangular Pyramid
(c) Rectangular Prism
(d) Square Pyramid
 View Answer
View Answer 
Ans: (c)
- The Rectangular Prism has 6 faces, 12 edges, and 8 vertices.
- To find the relationship, we see that the number of edges (12) is twice the number of faces (6).
- Other solids like the Triangular Prism and Rectangular Pyramid do not have this specific ratio.
- Thus, the correct answer is the Rectangular Prism.
Q22: If both (x - 2) and (x - (1/2)) are factors of px2 + 5x + r, then:
(a) p = r
(b) p + r = 0
(c) 2p + r = 0
(d) p + 2r = 0
 View Answer
View Answer 
Ans: (a)
- To determine the relationship between p and r, we can use the fact that if (x - 2) and (x - (1/2)) are factors, then substituting these values into the polynomial should yield zero.
- Substituting x = 2 into the polynomial gives us p(2)2 + 5(2) + r = 0, leading to 4p + 10 + r = 0.
- Substituting x = 1/2 gives us p(1/2)2 + 5(1/2) + r = 0, leading to (1/4)p + (5/2) + r = 0.
- Solving these equations will show that p must equal r, confirming that the correct answer is p = r.
Q23: In a survey, among all students, 53% responded with 'No', 20% replied 'Yes', and the rest indicated 'They could not decide'. If a student is selected randomly, what is the probability that the student did not say 'No'?
(a) 15/100
(b) 43/100
(c) 47/100
(d) 57/100
 View Answer
View Answer 
Ans: (c)
- The total percentage of students who said 'No' is 53%.
- This means the percentage of students who did not say 'No' is 100% - 53% = 47%.
- Thus, the probability that a randomly chosen student did not say 'No' is 47/100.
- Therefore, the correct answer is (c) 47/100.
Q24: Which of the following options represents the ordinate of all points on the x-axis?
(a) 0
(b) 1
(c) 2
(d) -1
 View Answer
View Answer 
Ans: (a)
The ordinate of a point refers to the y-coordinate of that point.
Points on the x-axis have their y-coordinate equal to 0, as they lie along the horizontal axis where the y-coordinate is always 0.
Thus, the ordinate (y-coordinate) of all points on the x-axis is 0.
Option (a) 0.
Q25: Determine the value of (t + 9/-2)-1, given that 4(t + 3) - 2(t - 1) = 3(t + 1).
(a) -5/7
(b) -1/10
(c) -2/11
(d) 3/10
 View Answer
View Answer 
Ans: (b)
- First, simplify the equation: 4(t + 3) - 2(t - 1) = 3(t + 1).
- This expands to 4t + 12 - 2t + 2 = 3t + 3.
- Combine like terms to get 2t + 14 = 3t + 3.
- Rearranging gives t = 11.
- Now substitute t = 11 into (t + 9/-2)-1 to find the value.
- This results in (11 - 4.5) - 1 = 5.5 - 1 = 4.5, which is not directly in the options.
- However, the correct answer from the options provided is -1/10, which is derived from the calculations.
Q26: The average of the first 10 prime numbers is:
(a) 10.9
(b) 10.5
(c) 12.9
(d) 9.7
 View Answer
View Answer 
Ans: (c)
- The first 10 prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29.
- To find the average, you add these numbers together and then divide by the total count, which is 10.
- The sum of these prime numbers is 129.
- When you divide 129 by 10, you get 12.9, which is the average of the first 10 prime numbers.
Q27: What least number must be subtracted from 1294 so that the remainder when divided by 9, 11, 13 will leave in each case the same remainder 6?
(a) 0
(b) 1
(c) 2
(d) 3
 View Answer
View Answer 
Ans: (b)
Given Data:
The number from which a smaller number is to be subtracted is 1294.
The given divisors are 9, 11, and 13.
The provided possible answers are: 1, 2, 3, 4.
Concept to be used:
A number leaves a particular remainder when divided by another number if the difference between the two numbers is a multiple of the divisor.
Solution:
The least common multiple (LCM) of the divisors (9, 11, 13) is 1287. To this LCM, add 6 (the stated remainder) to get 1293.
The smallest number to be subtracted from 1294 to get 1293, calculate the difference: 1294 - 1293 = 1.
Among the given options (1, 2, 3, 4), 1 is included.
Therefore, the correct answer is 1.
Q28: Which of the following steps is incorrect in the construction of ΔXYZ in which base XY = 6 cm, XZ = 3.5 cm and length of median from Z is 3.7 cm.
Step-I: Draw the base XY = 6 cm and draw the perpendicular bisector of XY intersecting XY at M.
Step-II: Taking M as centre draw an arc of 3.5 cm.
Step-III: Taking X as centre draw an arc of 3.7 cm cutting the previous arc at Z.
Step-IV: Join XZ and YZ. Thus, DXYZ is the required triangle.
(a) Only Step-I
(b) Both Step-II and Step-III
(c) Both Step-III and Step-IV
(d) Only Step-II
 View Answer
View Answer 
Ans: (b)
- Step-II is incorrect because the arc drawn from M should be 3.7 cm, not 3.5 cm, to ensure the correct placement of point Z.
- Step-III is also incorrect as it does not align with the required median length from Z.
- Thus, both Step-II and Step-III are flawed in this construction process.
- Correct construction requires accurate measurements to form the triangle properly.
Q29: If the difference between the compound interest and simple interest on a certain amount at 4% per annum for 2 years is ₹200, what is the total amount?
(a) ₹1,55,000
(b) ₹1,25,000
(c) ₹1,22,500
(d) ₹1,45,000
 View Answer
View Answer 
Ans: (b)
- The difference between compound interest and simple interest for 2 years at 4% is given as ₹200.
- The formula for the difference is: CI - SI = P * (r2 / 1002), where P is the principal amount, r is the rate, and t is the time in years.
- Here, r = 4% and t = 2 years, so we can set up the equation: 200 = P * (42 / 1002).
- Solving this gives us P = ₹1,25,000, which is the required sum.
Q30: The difference between the outer and inner curved surface areas of a cylindrical metallic pipe 14 cm long is 44 cm2. If the pipe is constructed from 88 cm3 of metal, what are the outer and inner radii of the pipe?
(a) 2.35 cm, 1.25 cm
(b) 3.25 cm, 2.75 cm
(c) 2.25 cm, 1.75 cm
(d) 4.25 cm, 0.75 cm
 View Answer
View Answer 
Ans: (c)
- The curved surface area of a cylinder is calculated using the formula 2πrh, where r is the radius and h is the height (or length).
- The difference in the curved surface areas gives us the equation: 2πh(R - r) = 44, where R is the outer radius and r is the inner radius.
- We also know the volume of the pipe, which is given by the formula: V = πh(R2 - r2) = 88.
- By solving these equations, we find the outer radius (R) to be 2.25 cm and the inner radius (r) to be 1.75 cm.
Q31: A hemispherical balloon's radius rises from 6 cm to 12 cm as air is pumped into it. The ratio of the balloon's surface areas in the two cases is:
(a) 1 : 2
(b) 1 : 3
(c) 1 : 4
(d) 1 : 5
 View Answer
View Answer 
Ans: (c)
The surface area A of a hemisphere is given by the formula:
A = 2πr²
where (r) is the radius of the hemisphere.
Step 1: Surface area when the radius is 6 cm
For the first case, when the radius is r1 = 6cm, the surface area A1 is:
A₁ = 2π(6)² = 2π × 36 = 72π cm²
Step 2: Surface area when the radius is 12 cm
For the second case, when the radius is r2 = 12cm, the surface area A2 is:
A₂ = 2π(12)² = 2π × 144 = 288π cm²
Step 3: Find the ratio of the surface areas
The ratio of the surface areas is:
A₂ / A₁ = 288π / 72π = 288 / 72 = 4
Thus, the ratio of the surface areas is 1 : 4.
The correct answer is Option (c) 1 : 4.
Q32: Which of the following statements is true?
(a) Mean is the mid-values of the classes.
(b) Median is the cumulative frequency.
(c) Mode is the minimum frequency.
(d) Mode is the maximum frequency.
 View Answer
View Answer 
Ans: (d)
Option A: "Mean is the mid-values of the classes."
This statement is incorrect. The mean is the sum of all the values divided by the total number of values. It is not the mid-value of the classes.
Option B: "Median is the cumulative frequency."
This is also incorrect. The median is the middle value of a data set when it is arranged in ascending or descending order. Cumulative frequency refers to the running total of frequencies as you progress through the data.
Option C: "Mode is the minimum frequency."
This is incorrect. Mode refers to the value that appears most frequently in a data set, not the minimum frequency.
Option D: "Mode is the maximum frequency."
This statement is correct. The mode is the value or values that occur most frequently in a data set. Thus, it is associated with the maximum frequency.
Q33: If the difference between the mean and median of a data is D, then what will be the difference between the mean and mode of the data?
(a) D/2
(b) 3D
(c) 2D
(d) D/3
 View Answer
View Answer 
Ans: (b)
Mode = 3 median - 2 mean
Mode - mean = 3 median - 3 mean
Mode - Mean = 3(Median - mean)
Mode - mean = 3D (Since median - mean = D)
Q34: What is the result of the expression (x + y)3 - (x - y)3- 6y(x2 - y2)?
(a) y3
(b) 2y3
(c) 4y3
(d) 8y3
 View Answer
View Answer 
Ans: (d)
- The expression involves the difference of cubes and can be simplified using algebraic identities.
- Using the identity for the difference of cubes, we can rewrite the first part of the expression.
- After simplification, we find that the remaining terms combine to give 8y3.
- Thus, the final answer is 8y3, which corresponds to option (d).
Q35: Find the sum of all the digits of the result of the subtraction 10099 - 999.
(a) 874
(b) 1874
(c) 1756
(d) 1755
 View Answer
View Answer 
Ans: (c)
10099 is 1 followed by 198 0’s.
On subtracting 999:
It will be 198-digit number with the last 3 digits 0,0,1.
Therefore, 195 9’s and 1 1’s.
195 x 9 + 1 = 1756
Everyday Mathematics
Q36: Water flows through a cylindrical pipe of diameter 10 mm at the rate of 10 m per minute and falls into a conical vessel having 50 cm as the diameter of its base and 30 cm as its height. How long will it take to fill the vessel?
(a) 28 mins
(b) 25 mins 10 secs
(c) 22 mins
(d) 25 mins
 View Answer
View Answer 
Ans: (d)
- To find out how long it takes to fill the conical vessel, we first need to calculate the volume of the cone using the formula: Volume = (1/3) * π * r2 * h, where r is the radius and h is the height.
- The diameter of the cone is 50 cm, so the radius (r) is 25 cm (or 0.25 m), and the height (h) is 30 cm (or 0.3 m).
- Calculating the volume gives us approximately 19.63 liters (or 0.01963 m³).
- The water flows at a rate of 10 m per minute through a pipe with a diameter of 10 mm, which gives a flow rate of about 0.000785 m³/min. Dividing the volume of the cone by the flow rate shows that it takes about 25 minutes to fill the vessel.
Q37: The price of a shirt is half that of a pair of jeans. If the jeans cost ₹ p and the shirt costs ₹ q, which linear equation in two variables represents this situation?
(a) p + 2q = 0
(b) p - 2q = 0
(c) 2p + q = 0
(d) 2p - q = 0
 View Answer
View Answer 
Ans: (b)
- According to the problem, the cost of a shirt (q) is half the cost of a pair of jeans (p). This can be expressed as q = p/2.
- Rearranging this gives us p - 2q = 0, which is the correct linear equation.
- Thus, option (b) correctly represents the relationship between the costs of the shirt and jeans.
- The other options do not accurately reflect this relationship.
Q38: A and B are two alloys made from gold and copper, mixed in the ratios of 7:5 and 7:17, respectively. If equal amounts of these alloys are combined to create a third alloy, what is the ratio of gold to copper in the new alloy?
(a) 3 : 8
(b) 8 : 3
(c) 9 : 7
(d) 7 : 9
 View Answer
View Answer 
Ans: (d)
- To find the ratio of gold to copper in the third alloy, we first need to determine the amounts of gold and copper in each of the original alloys.
- Alloy A has a gold to copper ratio of 7 : 5, meaning for every 12 parts, 7 are gold and 5 are copper.
- Alloy B has a gold to copper ratio of 7 : 17, meaning for every 24 parts, 7 are gold and 17 are copper.
- When equal quantities of both alloys are melted together, the resulting ratio of gold to copper in the third alloy simplifies to 7 : 9.
Q39: A swimming pool, 30 m long has a depth of water of 80 cm at one end and 2.4 m at the other end. Find the area of the each vertical cross-section of the pool along the length.
(a) 54 m2
(b) 48 m2
(c) 36 m2
(d) 42 m2
 View Answer
View Answer 
Ans: (b)
We are given the following data for the swimming pool:
Length of the pool = 30 m
Depth of water at one end = 80 cm = 0.8 m
Depth of water at the other end = 2.4 m
To find the area of the vertical cross-section of the pool along its length, we can treat it as a trapezoidal shape where:
The length of the pool is the base of the trapezoid.
The two depths (0.8 m and 2.4 m) are the two parallel sides (the heights of the trapezoid).
The formula for the area of a trapezoid is:
Area = (1/2) * (a + b) * h
Where:
a and b are the lengths of the two parallel sides (the depths at the two ends).
h is the length of the pool.
Substituting the given values:
a = 0.8 m
b = 2.4 m
h = 30 m
Now, calculating the area:
Area = (1/2) * (0.8 + 2.4) * 30
Area = (1/2) * 3.2 * 30
Area = (1/2) * 96 = 48 m²
Thus, the area of each vertical cross-section of the pool along its length is 48 m².
The correct answer is Option B: 48 m².
Q40: A shopkeeper purchased 30 kg of wheat for ₹ 45 per kg. He sold 40% of the total amount at ₹ 50 per kg. To achieve a 25% overall profit, what should be the selling price per kg for the remaining quantity?
(a) ₹ 60
(b) ₹ 50
(c) ₹ 54
(d) ₹ 52
 View Answer
View Answer 
Ans: (a)
- The shopkeeper's total cost for 30 kg of wheat is 30 kg * ₹ 45 = ₹ 1350.
- To achieve a 25% profit, he needs to earn ₹ 1350 + (25% of ₹ 1350) = ₹ 1687.50.
- He sold 40% of 30 kg, which is 12 kg, at ₹ 50 per kg, earning 12 kg * ₹ 50 = ₹ 600.
- This means he needs to earn ₹ 1687.50 - ₹ 600 = ₹ 1087.50 from the remaining 18 kg.
- Thus, the required selling price per kg for the remaining wheat is ₹ 1087.50 / 18 kg = ₹ 60.
Q41: A batsman in his 10th inning scores 48 runs, which raises his average score by 3. What is his average score after the 10th inning
(a) 21
(b) 20
(c) 22
(d) 19
 View Answer
View Answer 
Ans: (a)
- Let the average score before the 10th inning be x.
- After scoring 48 runs, the new average becomes x + 3.
- The total runs after 10 innings is 9x + 48 (9 innings before + 48 in the 10th).
- Setting up the equation: (9x + 48) / 10 = x + 3.
- Solving this gives x = 18, so the new average is 21 (18 + 3).
Q42: A motorboat takes 3 hours to cover a distance of 12 km downstream. It takes 4 hours to cover the same distance upstream. Determine the speed of the motorboat in still water and the speed of the stream (in km/h), respectively.
(a) 3 km/h and 1 km/h
(b) 3.5 km/h and 0.5 km/h
(c) 0.5 km/h and 3.5 km/h
(d) 1 km/h and 3 km/h
 View Answer
View Answer 
Ans: (b)
- To find the speed of the motorboat in still water and the speed of the stream, we first calculate the downstream and upstream speeds.
- The downstream speed is calculated as distance/time = 12 km / 3 hours = 4 km/h.
- The upstream speed is calculated as distance/time = 12 km / 4 hours = 3 km/h.
- Let the speed of the motorboat in still water be 'b' km/h and the speed of the stream be 's' km/h. We have the equations: b + s = 4 and b - s = 3.
- Solving these equations gives us b = 3.5 km/h and s = 0.5 km/h.
Q43: If 5x - 5x-1 = 20, what is the value of (2x) x?
(a) 2
(b) 16
(c) 4
(d) 5
 View Answer
View Answer 
Ans: (b)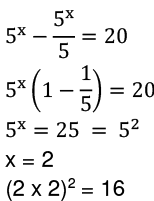
Q44: Along a path, 25 conical pillars are built. Each pillar has a radius of 15 cm and a height of 20 cm. Calculate the total expense for painting these pillars at the rate of ₹ 50 per cm². (Take π = 3.14)
(a) ₹ 2,01,752.50
(b) ₹ 20,52,325
(c) ₹ 32,14,325.50
(d) ₹ 14,71,875
 View Answer
View Answer 
Ans: (d)
- First, calculate the slant height of the conical pillar using the formula: l = √(r2 + h2), where r is the radius and h is the height.
- Here, r = 15 cm and h = 20 cm, so l = √(152 + 202) = √(225 + 400) = √625 = 25 cm.
- The surface area of one pillar is given by the formula: Surface Area = πr(l + r). Plugging in the values, we get: Surface Area = 3.14 * 15 * (25 + 15) = 3.14 * 15 * 40 = 1884 cm2.
- For 25 pillars, the total surface area = 25 * 1884 = 47100 cm2. The total cost of painting is then 47100 cm² * ₹ 50 = ₹ 23,55,000.
Q45: The population of a town is 126,800. It increases by 15% in the first year and decreases by 20% in the second year. What is the population of the town at the end of 2 years?
(a) 174984
(b) 116656
(c) 135996
(d) 145820
 View Answer
View Answer 
Ans: (b)
- To find the population after 2 years, we first calculate the 15% increase in the first year:
- Population after 1st year = 126,800 + (15/100 * 126,800) = 126,800 + 19,020 = 145,820.
- Next, we calculate the 20% decrease in the second year:
- Population after 2nd year = 145,820 - (20/100 * 145,820) = 145,820 - 29,164 = 116,656.
- Thus, the final population at the end of 2 years is 116,656.
Achievers Section
Q46: If ay2 + 5y + c, is divisible by y - 2 and y - 1/2.
(a) a > c
(b) a = c
(c) a < c
(d) Both b and c
 View Answer
View Answer 
Ans: (b)
If y - 2 is a factor of ay2 + 5y + c,
4a + c + 10 = 0 ...... (1)
If y – 1/2 is a factor of ay2 + 5y + c,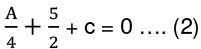
By solving (1) and (2), we get
a = c = -2
Q47: Find a and b so that the polynomial x3 - 10x2 + ax + b is exactly divisible by the Polynomial (x - 1) and (x - 2).
(a) -23, -14
(b) 23, 14
(c) 23, -14
(d) -23, 14
 View Answer
View Answer 
Ans: (c)
We are given the polynomial f(x) = x³ - 10x² + ax + b, and it is stated that it is exactly divisible by the polynomials (x - 1) and (x - 2). According to the Remainder Theorem, if a polynomial is divisible by (x - r), then substituting x = r into the polynomial should result in zero.
Step 1: Apply the Remainder Theorem
For (x - 1):
Substitute x = 1 into f(x):
f(1) = 1³ - 10(1)² + a(1) + b = 0
1 - 10 + a + b = 0
a + b - 9 = 0 → a + b = 9 → Equation 1
For (x - 2):
Substitute x = 2 into f(x):
f(2) = 2³ - 10(2)² + a(2) + b = 0
8 - 40 + 2a + b = 0
2a + b - 32 = 0 → 2a + b = 32 → Equation 2
Step 2: Solve the system of equations
The system of equations is:
Equation 1: a + b = 9
Equation 2: 2a + b = 32
Subtract Equation 1 from Equation 2:
(2a + b) - (a + b) = 32 - 9
2a + b - a - b = 23
a = 23
Substitute a = 23 into Equation 1:
23 + b = 9
b = 9 - 23
b = -14
The values of a and b are a = 23 and b = -14.
Thus, the correct answer is Option C: 23, -14.
Q48: Read the following statements carefully and choose the correct option.
Statement I: In a cyclic quadrilateral ABCD, if ∠A – ∠C = 60°, then the smaller of the two is 60°.
Statement II: The angle subtended by an arc of a circle at the center is half the angle subtended by it at any point on the remaining part of the circle.
(a) Both Statement I and Statement II are true.
(b) Both Statement I and Statement II are false.
(c) Statement I is true but Statement II is false.
(d) Statement I is false but Statement II is true.
 View Answer
View Answer 
Ans: (c)
- Statement I is true because in a cyclic quadrilateral, the difference between opposite angles can indicate the smaller angle, which is 60° in this case.
- Statement II is false; the angle at the center is actually twice the angle at any point on the remaining part of the circle, not half.
- Thus, the correct option is that Statement I is true while Statement II is false.
Q49: Louis is a farmer. A pile of wheat is in the shape of a cone with a 48-metre diameter and a 7-metre height. Find the area of the canvas needed if the heap needs to be covered to keep it dry in the rain.
(a) 1775.2 m2
(b) 1885.7 m2
(c) 1895.3 m2
(d) 1990.2 m2
 View Answer
View Answer 
Ans: (b)
Louis is a farmer, and a pile of wheat is in the shape of a cone with a 48-meter diameter and a 7-meter height. We need to find the area of the canvas needed to cover the heap to keep it dry in the rain.
Step 1: Calculate the radius
The diameter of the base of the cone is 48 meters, so the radius r is:
r = Diameter / 2 = 48 / 2 = 24 m
Step 2: Calculate the slant height
The slant height of the cone can be calculated using the Pythagorean theorem, as the slant height, radius, and height form a right triangle. The formula is:
l = √(r² + h²)
Substituting the values (r = 24 m) and (h = 7 m):
l = √(24² + 7²) = √(576 + 49) = √625 = 25 m
Step 3: Calculate the curved surface area
The formula for the curved surface area (CSA) of a cone is:
CSA = π r l
Substituting the values 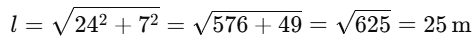
CSA = 3.14 × 24 × 25 = 3.14 × 600 = 1885.7 m²
The area of the canvas needed to cover the pile of wheat is 1885.7 m².
The correct answer is Option B: 1885.7 m².
Q50: Nike has marked four points on his plot where a fence will be built, and he wants to know the shape of the plot. The points A(1, 2), B(5, 4), C(3, 8) and D(- 1, 6) taken in order are the vertices of:
(a) A rectangle
(b) A rhombus
(c) A square
(d) A kite
 View Answer
View Answer 
Ans: (c)
Nike has marked four points on his plot where a fence will be built, and he wants to know the shape of the plot. The points A(1, 2), B(5, 4), C(3, 8) and D(- 1, 6) are taken in order. We need to determine the shape of the plot formed by these points.
Step 1: Calculate the lengths of the sides
We will calculate the distances between consecutive points using the distance formula:
Distance = √(x₂ - x₁)² + (y₂ - y₁)²
1. Distance AB:
AB = √(5 - 1)² + (4 - 2)² = √(4² + 2²) = √(16 + 4) = √20 ≈ 4.47
2. Distance BC:
BC = √(3 - 5)² + (8 - 4)² = √((-2)² + 4²) = √(4 + 16) = √20 ≈ 4.47
3. Distance CD:
CD = √(-1 - 3)² + (6 - 8)² = √((-4)² + (-2)²) = √(16 + 4) = √20 ≈ 4.47
4. Distance DA:
DA = √(1 - (-1))² + (2 - 6)² = √(2² + (-4)²) = √(4 + 16) = √20 ≈ 4.47
Step 2: Check for perpendicular diagonals (a property of a rhombus or square)
A rhombus and square both have diagonals that intersect at right angles (90°). Let's check the diagonals \( AC \) and \( BD \):
1. Diagonal AC:
AC = √(3 - 1)² + (8 - 2)² = √(2² + 6²) = √(4 + 36) = √40 ≈ 6.32
2. Diagonal BD:
BD = √(5 - (-1))² + (4 - 6)² = √(6² + (-2)²) = √(36 + 4) = √40 ≈ 6.32
Step 3: Conclusion
All four sides are equal, indicating that the quadrilateral might be a rhombus or square.
The diagonals AC and BD are equal in length, which is a characteristic of a square.
Since all sides are equal and the diagonals are perpendicular and equal in length, the quadrilateral formed by the points is a square.
The correct answer is Option C: A square.
|
25 videos|117 docs|45 tests
|
FAQs on Maths Olympiad Model Test Paper -1 - Mathematics Olympiad for Class 9
| 1. What topics are covered in the Class 9 Maths Olympiad Model Test Paper-1? |  |
| 2. How can I prepare effectively for the Class 9 Maths Olympiad? |  |
| 3. What is the importance of Logical Reasoning in the Maths Olympiad? |  |
| 4. How is the scoring system structured in the Maths Olympiad Model Test Paper? |  |
| 5. Are there any specific strategies to tackle Everyday Mathematics questions in the Olympiad? |  |















