Maths Olympiad Previous Year Paper -1 | Olympiad Preparation for Class 10 PDF Download
| Table of contents |

|
| Logical Reasoning |

|
| Mathematical Reasoning |

|
| Everyday Mathematics |

|
| Achievers Section |

|
Note: The questions provided in this document are similar to the questions that were asked in the actual Olympiad exam. So, we recommend you study these for your Olympiad preparation
Logical Reasoning
Q1: In the given Venn diagram, circle represents students living in Delhi, triangle represents students who use metro for transportation, rectangle represents students who like Mathematics. Which number represents students who live in Delhi and use metro for transportation and like Mathematics?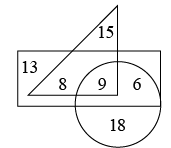 (a) 18
(a) 18
(b) 8
(c) 9
(d) 13
 View Answer
View Answer 
Ans: (c)
The region common to all three shapes is 9.
Q2: Select the number which will complete the given series.
2, 7, 22, 67, ?, 607
(a) 192
(b) 202
(c) 127
(d) 232
 View Answer
View Answer 
Ans: (b)
The pattern followed is: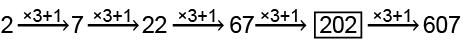
Q3: Select the box(es) that is/are similar to the box formed, when the given sheet is folded.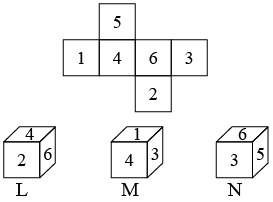 (a) L only
(a) L only
(b) Both L and M
(c) N only
(d) Both L and N
 View Answer
View Answer 
Ans: (d)
The numbers on opposite faces are : (1, 6), (2, 5) and (3, 4).
Q4: Six people A, B, C, D, E, and F are sitting on the ground in a hexagonal shape. All the sides of the hexagon so formed are of the same length. A is not adjacent to B or C; D is not adjacent to C or E; B and C are adjacent; F is in the middle of D and C. Which of the following is not a correct neighbor pair?
(a) A and F
(b) D and F
(c) B and E
(d) C and F
 View Answer
View Answer 
Ans: (a)
There can be two possible sitting arrangements. 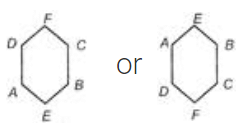
So, A and F are not a neighbour pair.
Q5: A postman was returning to the post office, which was in front of him to the north. When the post office was 100 metres away from him, he turned to the left and moved 50 metres to deliver the last letter at Shantivilla. He then moved in the same direction for 40 metres, turned to his right and moved 100 metres. How many metres was he away from the post office?
(a) 0
(b) 90
(c) 150
(d) 100
 View Answer
View Answer 
Ans: (b)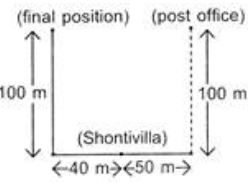 So distance between post office and post man = 40 + 50 = 90 m
So distance between post office and post man = 40 + 50 = 90 m
Q6: How many symbols and numbers are there in the sequence which are either immediately preceded or immediately followed by the letter that is from the first half of the English alphabet?
Sequence:
2 P J @ 8 $ L B I V # Q 6 5 G W 9 K C D 3 © ? £ 5 F R 7 A Y 4
(a) 6
(b) 7
(c) 8
(d) 9
 View Answer
View Answer 
Ans: (c)
Q7: All the faces of a cube are painted with blue color. Then it is cut into 125 small equal cubes. How many small cubes will be formed having no face colored?
(a) 27
(b) 8
(c) 16
(d) 24
 View Answer
View Answer 
Ans: (a)
Number of face with no face colored = 27
Q8: If ‘P’ represents ‘÷’, ‘Q’ represents ‘+’, ‘R’ represents ‘×’, and ‘S’ represents ‘–’, which of the following statements is accurate?
(a) 5 R 6 Q 8 P 2 S 9 = 25
(b) 4 R 6 Q 8 P 4 S 9 = 14
(c) 5 R 3 Q 8 P 2 S 7 = 10
(d) 4 R 3 Q 8 P 2 S 7 = 12
 View Answer
View Answer 
Ans: (a)
- First, we need to replace the symbols with their meanings: R = ×, Q = +, P = ÷, S = –.
- For option (a): 5 R 6 Q 8 P 2 S 9 becomes 5 × 6 + 8 ÷ 2 – 9.
- Calculating step-by-step: 5 × 6 = 30, then 30 + 8 = 38, next 8 ÷ 2 = 4, so 38 – 4 = 34, and finally 34 – 9 = 25.
- This confirms that option (a) is correct as it equals 25.
Q9: Ashok has two vessels which contain 720 ml and 405 ml of milk respectively. Milk in each vessel is poured into glasses of equal capacity to their brim. Find the minimum number of glasses which can be filled with milk.
(a) 45
(b) 35
(c) 25
(d) 30
 View Answer
View Answer 
Ans: (c)
Q10: If the first and the last digit of each of the following numbers are interchanged, and one is added to the middle digit, and then numbers are arranged in descending order, what is the sum of the digits of the middle number in the new arrangement formed?
(a) 14
(b) 12
(c) 13
(d) 16
 View Answer
View Answer 
Ans: (c)
- First, we interchange the first and last digits of each number:
- 246 becomes 642, 525 becomes 525, 432 becomes 234, 726 becomes 627, and 283 becomes 382.
- Next, we add 1 to the middle digit of each number: 642 becomes 652, 525 becomes 535, 234 becomes 244, 627 becomes 637, and 382 becomes 392.
- Now, we arrange these numbers in descending order: 652, 637, 535, 392, 244.
- The middle number in this arrangement is 535, and the sum of its digits (5 + 3 + 5) is 13.
Q11: Taxi charges in a city consist of fixed charges and the remaining depending upon the distance travelled in kilometres. If a person travels 70 km and he pays Rs. 500, for travelling 100 km he pays Rs. 680. What is the rate per kilometre?
(a) 6
(b) 8
(c) 10
(d) 7
 View Answer
View Answer 
Ans: (a)
Q12: A bicycle wheel makes 5000 revolutions in moving 11 km. What is the radius of the wheel?
(a) 45 cm
(b) 25 cm
(c) 35 cm
(d) None of these
 View Answer
View Answer 
Ans: (c)
Q13: A solid sphere of copper with a radius of 10.5 cm is melted, and right cones with a radius of 3.5 cm and height of 3 cm are made from the material. How many cones can be made?
(a) 136
(b) 126
(c) 156
(d) 146
 View Answer
View Answer 
Ans: (b)
Q14: In question three words are given, which have something in common among themselves. Out of four given alternatives choose the most appropriate description about these words.
Majlis : Diet : Knesset
(a) They are old names of certain countries
(b) These are various food eaten in various countries
(c) These are foreign languages
(d) These are Parliaments of different countries
 View Answer
View Answer 
Ans: (d)
Q15: Study the given information carefully and answer the following question.
(i) ‘A + B’ means ‘A is the mother of B’.
(ii) ‘A × B’ means ‘A is the father of B’.
(iii) ‘A ÷ B’ means ‘A is the son of B’.
(iv) ‘A – B’ means ‘A is the daughter of B’.
How is G related to L in the expression G × H + K – L?
(a) Grandfather
(b) Father-in-law
(c) Father
(d) Son-in-law
 View Answer
View Answer 
Ans: (b)
G ×× H + K – L means G is the father of H, who is mother of K.
Also, K is the daughter of L.
So, L is the husband of H. Hence, G is the father-in-law of L.
Mathematical Reasoning
Q16: If the solution of the pair of linear equations (2x - 3y = 13) and (7x - 2y = 20) satisfies the equation (y = mx + 7), then the value of (m) is _______.
(a) 5
(b) -5
(c) -10
(d) 14
 View Answer
View Answer 
Ans: (b)
- To find the value of m, we first need to solve the given linear equations.
- By solving (2x - 3y = 13) and (7x - 2y = 20), we can find the values of x and y.
- After finding y, we substitute it into the equation (y = mx + 7) to express m in terms of x.
- Through this process, we determine that the value of m is -5.
Q17: In an arithmetic progression, a1, a2, a3, a4, a5 are the first five terms. Given that a1 + a3 + a5 = –12 and a1·a2·a3 = 8, what is the common difference?
(a) 2
(b) -3
(c) 4
(d) -5
 View Answer
View Answer 
Ans: (b)
- In an arithmetic progression (A.P.), the terms can be expressed as: a1, a1 + d, a1 + 2d, a1 + 3d, a1 + 4d, where d is the common difference.
- From the equation a1 + a3 + a5 = –12, substituting the terms gives: a1 + (a1 + 2d) + (a1 + 4d) = –12, simplifying to 3a1 + 6d = –12.
- From a1·a2·a3 = 8, substituting gives: a1(a1 + d)(a1 + 2d) = 8.
- Solving these equations leads to the common difference d = -3.
Q18: In how many ways can 480 be resolved into two factors?
(a) 18
(b) 12
(c) 24
(d) 36
 View Answer
View Answer 
Ans: (b)
480 = 25 x 31 x 51
Number of factors of 480 = (5 + 1) (1 + 1) (1 + 1) = 24.
Number of ways in which 480 can be resolved into two factors = 24/2 = 12
Q19: What must be subtracted from the polynomial f(x) = x4 + 2x3 - 13x2 - 12x + 21 so that the resulting polynomial is exactly divisible by x2 - 4x + 3?
(a) (x - 2)
(b) (2x - 3)
(c) (x + 3)
(d) (2x + 3)
 View Answer
View Answer 
Ans: (b)
Q20: Determine the value of a that makes the quadratic equation (a – 4) x2 + 2 (a – 4) x + 4 = 0 have equal roots.
(a) 8
(b) 4
(c) 6
(d) Both A and B
 View Answer
View Answer 
Ans: (d)
- For a quadratic equation to have equal roots, the discriminant must be zero.
- The discriminant is calculated as b2 - 4ac. Here, a = (a - 4), b = 2(a - 4), and c = 4.
- Setting the discriminant to zero gives us the equation: (2(a - 4))2 - 4(a - 4)(4) = 0.
- Solving this leads to the values of a being 4 and 8, which means both options A and B are correct.
Q21: A shopkeeper wants to use a minimum number of boxes at the same time all the boxes should contain the same no. of pencils. But each box must contain only one type of pencil. How many pencils per box should he pack if he wants to pack 612 orange pencils and 342 red pencils?
(a) 18
(b) 21
(c) 20
(d) 16
 View Answer
View Answer 
Ans: (a)
The required number is HCF of 612 and 342.
This number gives the maximum number of pencils in each box and the number of boxes with them be the least.
By using Euclid’s division algorithm, we have 612 = 342 × 1 + 270
342 = 270 × 1 + 72
270 = 72 × 3 + 54
72 = 54 × 1 + 18
54 = 18 × 3 + 0
Here we notice that the remainder is zero, and the divisor at this stage is 18.
∴ HCF of 612 and 342 is 18.
So, the shopkeeper can pack 18 pencils per box.
Q22: There are 78 boys and 45 girls in a class. These students are arranged in rows grouping in the Athletics event, each row consists of only either boys or girls, and every row contains an equal number of students. Find the minimum number of rows in which all the students can be arranged.
(a) 43
(b) 45
(c) 41
(d) 51
 View Answer
View Answer 
Ans: (c)
For the number of rows to be the least, the number of students in each row must be the highest.
The number of students in each row is a common factor of 78 and 45. The highest value is the HCF of 78 and 45, which is 3.
Minimum number of rows = 78/3 + 45/3 = 41
Q23: When two dice are rolled simultaneously, what is the probability that the absolute difference between the numbers displayed on the dice is 1?
(a) 5/18
(b) 1/36
(c) 1/6
(d) None of these
 View Answer
View Answer 
Ans: (a)
- The total possible outcomes when rolling two dice is 36 (6 sides on the first die multiplied by 6 sides on the second die).
- The favorable outcomes where the difference is 1 are: (1,2), (2,1), (2,3), (3,2), (3,4), (4,3), (4,5), (5,4), (5,6), (6,5). This gives us a total of 10 outcomes.
- The probability is calculated as the number of favorable outcomes divided by the total outcomes: 10/36, which simplifies to 5/18.
- Thus, the probability that the difference of the numbers shown on the dice is 1 is 5/18.
Q24: A cylindrical vessel with a diameter of 4 cm is partially filled with water. When 300 lead balls are added, the water level rises by 0.8 cm. What is the diameter of each ball?
(a) 0.8 cm
(b) 0.4 cm
(c) 0.2 cm
(d) None of these
 View Answer
View Answer 
Ans: (b)
- The volume of water displaced by the balls equals the volume of the balls themselves.
- The volume of the cylinder can be calculated using the formula: Volume = π × (radius)2 × height. Here, the radius is 2 cm (half of the diameter) and the height is 0.8 cm.
- Calculating the volume gives: Volume = π × (2 cm)2 × 0.8 cm = 3.2π cm3.
- Since there are 300 balls, the volume of one ball is: Volume of one ball = Total volume / Number of balls = (3.2π cm3) / 300.
- Using the formula for the volume of a sphere (V = 4/3 × π × (radius)3), we can find the radius of one ball and then double it to get the diameter, which results in a diameter of 0.4 cm.
Q25: Given ax2 + bx + c is a quadratic polynomial in x and leaves remainders 7, 12 and 19, respectively, when divided by (x + 1), (x + 2) and (x + 3). Find the value of a + b + c.
(a) 3
(b) 4
(c) 2
(d) 1
 View Answer
View Answer 
Ans: (a)
Let f(x) = ax2 + bx +c.
Given, f (− 1) = 7, f (− 2) = 12, f (−3) = 19
a −b + c = 7 .... (1)
4a − 2b + c = 12 ......(2)
9a − 3b + c = 19 ..........(3)
Solving these equations, we get, a = 1, b = -2, c = 4
Therefore, a + b + c = 3
Q26: Which of the following is a rational number?
(a) Sum of 2 + √3 and its inverse
(b) Square root of 20
(c) Square root of 7 + √3
(d) None of these
 View Answer
View Answer 
Ans: (a)
- The question asks for a rational number, which is a number that can be expressed as a fraction of two integers.
- Option (a) involves the sum of 2 and √3, which is not a rational number, but its inverse can be rational.
- Options (b) and (c) involve square roots of non-perfect squares, which are also irrational numbers.
- Thus, the correct answer is (a) because it includes the concept of an inverse that can yield a rational result.
Q27: There are three terms in AP, whose sum is 69 and the product is 11339. Find the common difference.
(a) 6
(b) -6
(c) 8
(d) Both a and b
 View Answer
View Answer 
Ans: (d)
Let the three terms of an AP be (a - d), a and (a + d).
The sum of these terms is 3a.
3a = 69
a = 23
Product of these three terms is
(a + d) a (a - d) = 11339
(23 + d) (23 - d) = 493
529 - d2 = 493 ⇒ d = ±6.
Taking d = 8, we get the terms as 17, 23 and 29.
Q28: If p(x) = x3 + 3x2 – 2x + 4, what is the value of p(2) + p(–2) – p(0)?
(a) 28
(b) 14
(c) 12
(d) 18
 View Answer
View Answer 
Ans: (a)
- First, calculate p(2): p(2) = 23 + 3(2)2 – 2(2) + 4 = 8 + 12 - 4 + 4 = 20.
- Next, calculate p(–2): p(–2) = (–2)3 + 3(–2)2 – 2(–2) + 4 = -8 + 12 + 4 + 4 = 12.
- Then, calculate p(0): p(0) = 03 + 3(0)2 – 2(0) + 4 = 4.
- Now, combine these results: p(2) + p(–2) – p(0) = 20 + 12 - 4 = 28.
Q29: Find the value of p for which the numbers 2p - 1, 3p + 1, 11 are in AP.
(a) 6
(b) 5
(c) 2
(d) 1
 View Answer
View Answer 
Ans: (c)
If the numbers a, b and c are in AP, then
b - a = c - b
2b = a + c
The given three numbers (2p - 1), (3p + 1) and 11 are in AP.
Then, 2(3p + 1) = (2p - 1) + 11
6p + 2 = 2p - 1 + 11
6p + 2 = 2p + 10
6p - 2p = 10 - 2
4p = 8
p = 2
So, the value of p is 2.
Q30: The sums of n terms of two arithmetic series are in the ratio 3n + 2 : 3n - 4. Find the ratio of their 10th terms.
(a) 59/53
(b) 53/59
(c) 51/53
(d) 59/51
 View Answer
View Answer 
Ans: (a)
Let the two arithmetic series be a, a + d, a + 2d .... and A, A + D, A + 2D, .... Given that,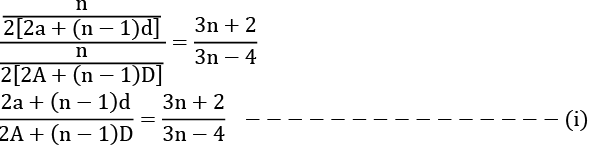
Ratio of the 10th terms of these series = 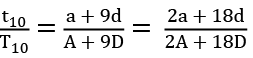
Putting n = 19 in (i), we have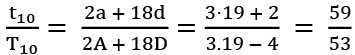
Q31: Arithmetic means are inserted between A and B; the sum of these means is (number of means + 1). How many means are there, if A + B = 91/42 and even number of Arithmetic means are inserted?
(a) 10
(b) 12
(c) 13
(d) 14
 View Answer
View Answer 
Ans: (b)
Q32: An examination consists of 100 questions. +4 are awarded for every correct option. If 2 marks are deducted for every wrong option and 1 mark is deducted for every question left, then a person scores 114. Instead, if 1 mark is deducted for every wrong option and 2 marks is deducted for every question left, then the person scores 136. Find the number of questions left unattempted by the person.
(a) 14
(b) 16
(c) 10
(d) 12
 View Answer
View Answer 
Ans: (a)
The equations are:
x + y + z = 100
4x - 2y - z = 114
4x - y - 2z = 136
On solving the equations
x = 50, y = 36, z = 14
Q33: If p(x) = x2 - 3x + p and q(x) = 2x2 + qx + 2 are the polynomials that share a common factor of x + 2, what are the values of p and q respectively?
(a) 10, 5
(b) -10, 5
(c) 10, -5
(d) -10, -5
 View Answer
View Answer 
Ans: (b)
- To find the values of p and q, we substitute x = -2 into both polynomials since x + 2 is a common factor.
- For p(x): p(-2) = (-2)2 - 3(-2) + p = 4 + 6 + p = 10 + p. Setting this to 0 gives p = -10.
- For q(x): q(-2) = 2(-2)2 + q(-2) + 2 = 8 + q(-2) + 2 = 10 + q(-2). Setting this to 0 gives q = 5.
- Thus, the values of p and q are -10 and 5 respectively.
Q34: Find the value of t when it is given that x2 − 24 − t(2x − 11) = 0 is a quadratic equation having equal roots.
(a) 3
(b) 8
(c) Both (a) and (b)
(d) 24
 View Answer
View Answer 
Ans: (c)
The equation is: x2 − 24 − 2tx + 11t = 0
For equal roots, discriminant must be 0
4t2 − 4(11t − 24) = 0
t2 − 11t + 24 = 0
(t − 3)(t − 8) = 0
Q35: Some students organized a picnic with a food budget of ₹500. However, 5 students could not attend, resulting in an increase of ₹5 in the food cost per person. How many students initially planned for the picnic?
(a) 15
(b) 20
(c) 25
(d) 30
 View Answer
View Answer 
Ans: (b)
- Let the initial number of students be x.
- The cost per student before 5 students dropped out is 500/x.
- After 5 students leave, the number of students becomes x - 5, and the new cost per student is 500/(x - 5).
- According to the problem, the new cost per student is ₹5 more than the old cost: 500/(x - 5) = 500/x + 5.
- Solving this equation gives x = 20, meaning 20 students initially planned for the picnic.
Everyday Mathematics
Q36: A, B, and C are three partners in a business. If two times A's investment equals three times B's capital, and B's capital is four times C's capital, what is B's share from a total profit of ₹ 29,700?
(a) ₹14,000
(b) ₹18,000
(c) ₹10,800
(d) ₹14,800
 View Answer
View Answer 
Ans: (c)
- Let A's investment be represented as 2x, B's as 3y, and C's as y.
- From the problem, we know that 2A = 3B and B = 4C, which gives us the relationships between their investments.
- By substituting the values, we find that B's share of the total profit is calculated based on the ratio of their investments.
- After calculating, B's share from the total profit of ₹ 29,700 comes out to be ₹ 10,800.
Q37: The average monthly salary of the workers in a garage is ₹8,500. If the average monthly salary of 7 mechanics is ₹10,000 and the average monthly salary of the rest is ₹7,800, what is the total number of workers in the garage?
(a) 18
(b) 20
(c) 22
(d) 24
 View Answer
View Answer 
Ans: (c)
- Let the total number of workers be N.
- The total salary of all workers is N × 8,500.
- The total salary of 7 mechanics is 7 × 10,000 = 70,000.
- The total salary of the remaining workers is (N - 7) × 7,800.
- Setting up the equation: N × 8,500 = 70,000 + (N - 7) × 7,800.
- Solving this gives N = 22.
Q38: Three caps and four bats together cost ₹257, while four caps and three bats together cost ₹324. What is the total cost of one cap and ten bats?
(a) ₹250
(b) ₹255
(c) ₹155
(d) ₹160
 View Answer
View Answer 
Ans: (c)
- Let the cost of one cap be C and one bat be B.
- From the first statement: 3C + 4B = 257.
- From the second statement: 4C + 3B = 324.
- By solving these two equations, we find C and B.
- After calculating, we find the cost of one cap and ten bats: C + 10B = 155.
Q39: A train measuring 150 m takes 10 seconds to completely pass another train that is 100 m long, which is approaching from the opposite direction. If the speed of the first train is 30 km/h, what is the speed of the second train?
(a) 54 km/h
(b) 60 km/h
(c) 72 km/h
(d) 36 km/h
 View Answer
View Answer 
Ans: (b)
- To find the speed of the second train, we first calculate the total distance covered when both trains pass each other, which is the sum of their lengths: 150 m + 100 m = 250 m.
- The time taken to pass is 10 seconds, so we can find the relative speed of both trains combined: Speed = Distance/Time = 250 m / 10 s = 25 m/s.
- Now, we convert the speed of the first train from km/h to m/s: 30 km/h = 30 * (1000 m / 3600 s) = 8.33 m/s.
- Using the formula for relative speed: Relative Speed = Speed of Train 1 + Speed of Train 2, we have 25 m/s = 8.33 m/s + Speed of Train 2.
- Solving for Speed of Train 2 gives us: Speed of Train 2 = 25 m/s - 8.33 m/s = 16.67 m/s, which converts back to km/h as 16.67 * (3600 s / 1000 m) = 60 km/h.
Q40: If the compound interest on a specific amount of money for 3 years at an annual rate of 10% is ₹993, what would be the simple interest on that same amount at the same rate and duration?
(a) ₹750
(b) ₹800
(c) ₹900
(d) None of these
 View Answer
View Answer 
Ans: (c)
- The formula for compound interest is used to calculate the interest earned on an investment over time, which in this case is ₹993 for 3 years at 10% per annum.
- The simple interest can be calculated using the formula: Simple Interest = (Principal × Rate × Time) / 100.
- Given that the compound interest is higher than simple interest, we can derive that the simple interest for the same principal, rate, and time will be ₹900.
- This shows that while compound interest accumulates more over time, the simple interest remains straightforward and is less than the compound interest in this scenario.
Q41: Priyanshu owns a motorcycle that has wheels with a diameter of 91 cm. The wheel contains 22 spokes. Calculate the length of the arc that lies between two neighboring spokes.
(a) 26 cm
(b) 13 cm
(c) 15 cm
(d) 18 cm
 View Answer
View Answer 
Ans: (b)
- To find the length of the arc between two spokes, we first need to calculate the circumference of the wheel using the formula: Circumference = π × diameter.
- Here, the diameter is 91 cm, so the circumference is approximately 3.14 × 91 cm = 285.34 cm.
- Since there are 22 spokes, the length of the arc between two adjoining spokes is the total circumference divided by the number of spokes: 285.34 cm / 22 ≈ 13 cm.
- Thus, the length of the arc between two spokes is 13 cm, which corresponds to option (b).
Q42: A hemispherical bowl with an internal diameter of 36 cm is filled with liquid. This liquid needs to be transferred into cylindrical bottles, each having a radius of 3 cm and a height of 9 cm. How many bottles will be needed to completely empty the bowl?
(a) 45
(b) 49
(c) 46
(d) 48
 View Answer
View Answer 
Ans: (d)
- The volume of the hemispherical bowl can be calculated using the formula: V = (2/3)πr³. Here, the radius (r) is half of the diameter, which is 18 cm.
- The volume of one cylindrical bottle is given by the formula: V = πr²h. For the bottle, the radius is 3 cm and the height is 9 cm.
- After calculating both volumes, divide the volume of the bowl by the volume of one bottle to find out how many bottles are needed.
- The final calculation shows that 48 bottles are required to empty the bowl.
Q43: In the Maths Olympiad of 2020 at Animal Planet, two representatives from the donkey’s side, while solving a quadratic equation, committed the following mistakes:
(i) One of them made a mistake in the constant term and got the roots as 5 and 9.
(ii) Another one committed an error in the coefficient of x and he got the roots as 12 and 4.
But in the meantime, they realized that they were wrong, and they managed to get it right jointly.
Find the quadratic equation.
(a) x2 + 4x + 14 = 0
(b) 2x2 = 7x – 24 = 0
(c) x2 – 14x + 48 = 0
(d) 3x2 – 17x + 52 = 0
 View Answer
View Answer 
Ans: (c)
- The roots 5 and 9 suggest a quadratic equation of the form (x - 5)(x - 9) = 0, which expands to x2 - 14x + 45 = 0.
- The roots 12 and 4 suggest another equation of the form (x - 12)(x - 4) = 0, which expands to x2 - 16x + 48 = 0.
- To find the correct quadratic equation, we need to combine the information from both mistakes.
- The correct quadratic equation that fits the roots derived from the mistakes is x2 - 14x + 48 = 0.
Q44: The cost of 2 burgers, 14 chocolates, and 5 pizzas is $400. The cost of 20 burgers, 7 chocolates, and 15 pizzas is $1270. Find the cost of 38 burgers and 25 pizzas (in $).
(a) 2196
(b) 2140
(c) 2104
(d) 1420
 View Answer
View Answer 
Ans: (b)
Let the cost of each burger be p.
Let the cost of each chocolate be c.
Let the cost of each pizza be z.
Then 2p + 14c + 5z = 400 ……….(1)
Also, 20p + 7c + 15z = 1270 ……….(2)
Multiply Eq. (2) by 2, we have
40p + 14c + 30z = 2540 ………(3)
Subtracting Eq. (1) from Eq. (3), we have
38p + 25z = 2140
Q45: The roots of the equation x2 + 3x – 10 = 0 are: 1
(a) 2, -5
(b) -2, 5
(c) 2, 5
(d) -2, -5
 View Answer
View Answer 
Ans: (a)
Given, x2 + 3x – 10 = 0
⇒ x2 + 5x – 2x – 10 = 0
⇒ x(x + 5) -2(x + 5) = 0
⇒ (x – 2) (x + 5) = 0
Zeroes are x – 2 = 0 or x + 5 = 0
∴ x = 2 or x = -5
Achievers Section
Q46: The following data is about a carrot farm for 10 years. In the nth year, the farmer produces 11n carrots. During the first 5 years, some carrots are eaten by rabbits. During the last 5 years, every year the number of carrots eaten by a rabbit is half the corresponding number in the first 5 years. In the fourth year, the farmer produces 36 carrots. How many carrots did he produce in the 9th year?
(a) 100
(b) 96
(c) 95
(d) 86
 View Answer
View Answer 
Ans: (c)
Every year in the first 5 years, the number of carrots that is eaten is y (say).
The number of carrots produced in the xth year = 11x - y
Number of carrots produced in 4th year = 36
⇒ 11(4) - y = 36 ⇒ y = 8
Number of fruits produced in xth year in the last 5 years = 11x - y/2
Number of fruits produced in the 9th year = 11(9) - 8/2 = 99 - 4 = 95
Q47: Find the equation of the line which passes through the point of intersection of the lines 2x - y + 5 = 0 and 5x + 3y -4 = 0 and is perpendicular to the line x - 3y + 21 = 0:
(a) 2x + y + 10 = 0
(b) 3x + y + 21 = 0
(c) 3x + y = 0
(d) 3y - x + 21 = 0
 View Answer
View Answer 
Ans: (c)
Q48: If α and β are the roots of the equation x2 + x + 1 = 0, then the equation whose roots are α19 and β7 is:
(a) x2 - x - 1 = 0
(b) x2 - x + 1 = 0
(c) x2 + x - 1 = 0
(d) x2 + x + 1 = 0
 View Answer
View Answer 
Ans: (d)
Q49: Find the equation of a line making intercepts 5 and 7 on the coordinate axes.
(a) 7x - 5y - 35 = 0
(b) 7x + 5y + 35 = 0
(c) 7x + 5y - 35 = 0
(d) 7x - 5y + 35 = 0
 View Answer
View Answer 
Ans: (c)
Given, x-intercept (a) = 5 and y-intercept (b) = 7
∴ The equation of the required line is x/a + y/b = 1
x/5 + y/7 = 1
7x + 5y - 35 = 0
Q50: A line is of length 10 and one of its endpoints is on (2, -4). If the abscissa of the other end be 10. Find its y coordinate.
(a) -10
(b) 3
(c) 2
(d) 1
 View Answer
View Answer 
Ans: (a)
Let the ordinate of the second point be y.
So, the first point is (2, -4) and the second is (10, y).
The distance between them must be 10.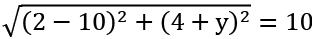
64 + y2 + 16 + 8y = 100
y2 + 8y − 20 = 0
y2 + 10y − 2y − 20 = 0
y · (y + 10) − 2 · (y + 10) = 0
(y + 10) · (y − 2) = 0
y = −10 or y = 2
|
70 videos|242 docs|187 tests
|
FAQs on Maths Olympiad Previous Year Paper -1 - Olympiad Preparation for Class 10
| 1. What topics are covered in the Class 10 Maths Olympiad exam? |  |
| 2. How can I prepare effectively for the Class 10 Maths Olympiad? |  |
| 3. What is the format of the Class 10 Maths Olympiad exam? |  |
| 4. Are there any recommended books or resources for the Class 10 Maths Olympiad preparation? |  |
| 5. How is the Class 10 Maths Olympiad exam scored? |  |















