Mathematics Olympiad Model Test Papers - 2 | Olympiad Preparation for Class 10 PDF Download
| Table of contents |

|
| Logical Reasoning |

|
| Mathematical Reasoning |

|
| Everyday Mathematics |

|
| Achievers Section |

|
Note: The questions provided in this document are similar to the questions that were asked in the actual Olympiad exam. So, we recommend you study these for your Olympiad preparation
Logical Reasoning
Q1: Select a figure from amongst the Answer Figures which will continue the same series as established by the five Problem Figures.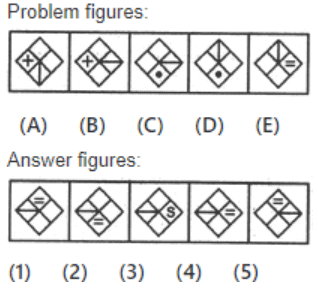
(a) 1
(b) 4
(c) 5
(d) 2
 View Answer
View Answer 
Ans: (b)
The line segment rotates through 90o and moves to the adjacent portion of the rhombus in an anti-clockwise direction in first, third, fifth, ... steps. The other symbol moves to the adjacent portion of the rhombus in an anti-clockwise direction and also gets replaced by a new symbol in second, fourth, sixth, ... steps.
Q2: Choose the figure which is different from the rest.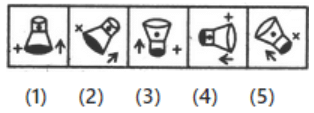 (a) 5
(a) 5
(b) 1
(c) 4
(d) 2
 View Answer
View Answer 
Ans: (c)
In all other figures, the arrow and the V sign lie towards the black end of the main figure.
Q3: Find the mirror of figure (X) letter, if the mirror is placed along dotted line MN.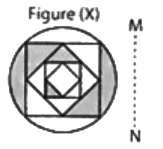 (a)
(a) 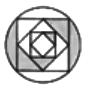 (b)
(b) 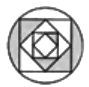 (c)
(c)  (d)
(d) 
 View Answer
View Answer 
Ans: (d)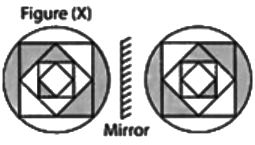 is the correct mirror image of the figure (X).
is the correct mirror image of the figure (X).
Q4: Select a suitable figure from the four alternatives that would complete the figure matrix.
(a) 3
(b) 4
(c) 2
(d) 1
 View Answer
View Answer 
Ans: (a)
In each column, the second figure (middle figure) is obtained by removing the upper part of the first figure (uppermost figure) and the third figure (lowermost figure) is obtained by vertically inverting the upper part of the first figure.
Q5: An electronic device rearranges numbers and words in a particular rule in each step. The following is an illustration of Input and steps of rearrangement:
Input: window 27 goods 43 door 17 open 32 shut 50
Step I: 17 window 27 goods 43 door open 32 shut 50
Step II: 17 window 27 shut goods 43 door open 32 50
Step III: 17 window 27 shut 32 goods 43 door open 50
Step IV: 17 window 27 shut 32 open goods 43 door 50
Step V: 17 window 27 shut 32 open 43 goods door 50
Step VI: 17 window 27 shut 32 open 43 goods 50 door
Step VI is the last step of the given input.
As per the rule followed in the above steps, which of the following will be the fourth step for the given input?
Input: cat 62 pull 81 the 22 34 bell
(a) 22 the 34 pull cat 62 81 bell
(b) the 24 cat 62 pull 81 bell
(c) 22 the cat 62 pull 81 34 bell
(d) 22 cat 62 pull 81 34 bell
 View Answer
View Answer 
Ans: (a)
- The input consists of words and numbers that need to be rearranged based on specific rules.
- In the steps provided, the numbers are moved to the front in ascending order while the words follow a specific sequence.
- For the new input, the fourth step involves moving the smallest number (22) to the front, followed by the next smallest (34), and then rearranging the remaining words and numbers accordingly.
- Thus, the correct fourth step for the new input is 22 the 34 pull cat 62 81 bell.
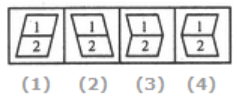
Q6: Select a suitable figure from the four alternatives that would complete the figure matrix.
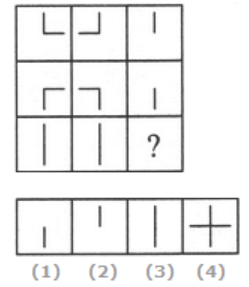
(a) 4
(b) 2
(c) 3
(d) 1
 View Answer
View Answer 
Ans: (c)
In each row, the third figure is a collection of the common elements (line segments) of the first and the second figures.
Q7: If ‘@’ represents ‘×’, ‘#’ represents ‘÷’, ‘*’ represents ‘+’, and ‘%’ represents ‘–’, which of the following statements is incorrect?
(a) 20 * 6 @ 9 # 3 % 8 = 30
(b) 18 # 6 @ 4 * 15 % 9 = 18
(c) 12 * 3 @ 27 # 3 % 16 = 23
(d) 19 * 5 % 8 @ 3 = 10
 View Answer
View Answer 
Ans: (d)
- To solve this, we need to replace the symbols with their meanings:
- For option (d): 19 * 5 % 8 @ 3 becomes 19 + 5 - 8 × 3.
- This simplifies to 19 + 5 - 24, which equals 0, not 10.
- Thus, option (d) is incorrect, while the others are correct when calculated.
Q8: Identify the figure that completes the pattern.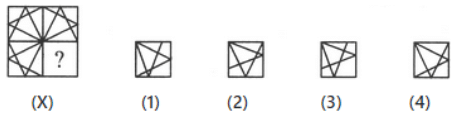 (a) 1
(a) 1
(b) 3
(c) 2
(d) 4
 View Answer
View Answer 
Ans: (d)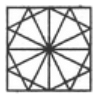
Q9: Six families M, N, O, P, Q and R are residing on different floors of a building. The ground floor is considered as the 1st floor and the top floor is the 6th floor.
Study the following information carefully and answer the given question.
(i) Family R is living above the floor of family M.
(ii) There are 4 families living between P and Q where Q is living on the 1st floor.
(iii) N is living just below the floor of family P.
(iv) Family O is living on an even-numbered floor but not directly above family
Which family is situated between family N and family R?
(a) M
(b) Q
(c) O
(d) P
 View Answer
View Answer 
Ans: (c)
- From the information, we know that Q is on the 1st floor.
- Since there are 4 families between P and Q, P must be on the 6th floor.
- N is just below P, so N is on the 5th floor.
- Family R is above M, and since O is on an even floor, O must be on the 2nd or 4th floor.
- Given the arrangement, O is on the 4th floor, making M on the 3rd floor and R on the 6th floor.
- Thus, the family between N (5th floor) and R (6th floor) is O (4th floor).
Q10: If ‘A $ B’ signifies A is the brother of B, ‘A @ B’ signifies A is the wife of B, ‘A # B’ signifies A is the daughter of B, and ‘A * B’ signifies A is the father of B, which of the following shows that U is the mother-in-law of P?
(a) P@Q$T#U@W
(b) P@W$QT#U
(c) P@Q$WT#U
(d) P@Q$T#W*U
 View Answer
View Answer 
Ans: (a)
- To determine that U is the mother-in-law of P, we need to analyze the relationships given in the options.
- In option (a), P is the wife of Q, Q is the brother of T, T is the daughter of U, and U is the wife of W. This means U is the mother of T, making her the mother-in-law of P.
- The other options do not establish this relationship clearly, as they either change the roles or do not connect U as the mother-in-law of P.
- Thus, option (a) correctly indicates that U is the mother-in-law of P.
Q11: If it is feasible to create a valid English word using the second, fifth, sixth, and eighth letters of the word GENEROUS, how many distinct words can be generated with these letters?
(a) 0
(b) 2
(c) 1
(d) More than 2
 View Answer
View Answer 
Ans: (d)
- The letters from the word GENEROUS are: E, R, O, and S (2nd, 5th, 6th, and 8th letters).
- These letters can be rearranged to form multiple words, such as ROSE and SORE.
- Since more than two valid words can be formed, the answer is More than 2.
- Thus, the correct option is (d).
Q12: Choose the figure which is different from the rest.
(a) 2
(b) 1
(c) 5
(d) 4
 View Answer
View Answer 
Ans: (b)
In all other figures, there are two small line segments towards the pin and three small line segments towards the arrow.
Q13: Find the number of triangles in the given figure.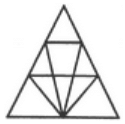 (a) 18
(a) 18
(b) 22
(c) 26
(d) 12
 View Answer
View Answer 
Ans: (a)
The figure may be labelled as shown.
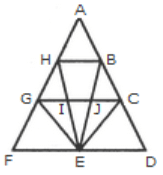 The simplest triangles are AHB, GHI, BJC, GFE, GIE, IJE, CEJ and CDE i.e. 8 in number.
The simplest triangles are AHB, GHI, BJC, GFE, GIE, IJE, CEJ and CDE i.e. 8 in number.
The triangles composed of two components each are HEG, BEC, HBE, JGE and ICE i.e. 5 in number.
The triangles composed of three components each are FHE, GCE and BED i.e. 3 in number.
There is only one triangle i.e. AGC composed of four components.
There is only one triangle i.e. AFD composed of nine components.
Thus, there are 8 + 5 + 3 + 1 + 1 = 18 triangles in the given figure.
Q14: A man walks 5 km toward the south and then turns to the right. After walking 3 km he turns to the left and walks 5 km. Now in which direction is he from the starting place?
(a) South-West
(b) West
(c) South
(d) North-East
 View Answer
View Answer 
Ans: (a)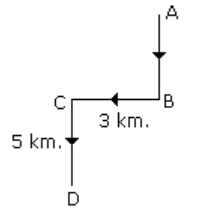 Hence required direction is South-West.
Hence required direction is South-West.
Q15: Some letters and numbers are encoded as shown below. What will be the code for 5KR7CM?  Number or letter Code While encoding the given number or letter, the following conditions are also taken into account.
Number or letter Code While encoding the given number or letter, the following conditions are also taken into account.
Conditions:
I. If any letter is surrounded by a number, it is coded as →.
II. If any letter is surrounded by another letter, it is coded as ↑.
What will be the code for 5KR7CM?
(a) $©ζ↑@*
(b) $©ζ→@*
(c) $©ζ+*@(
(d) $©ζ↑*@
 View Answer
View Answer 
Ans: (c)
- In the code for 5KR7CM, we analyze each character based on the given conditions.
- The number 5 is followed by the letter K, so K is surrounded by numbers, which means it is coded as →.
- Next, R is surrounded by letters K and 7, so it is coded as ↑.
- Finally, C is surrounded by letters M and 7, so it is coded as ↑.
- Thus, the complete code for 5KR7CM becomes $©ζ+*@(.
Mathematical Reasoning
Q16: The roots of the quadratic equation 13x² + 5x – 2 = 0 are:
(a) Real and equal
(b) Rational
(c) Real and distinct
(d) Not real
 View Answer
View Answer 
Ans: (c)
- The given equation is a quadratic equation of the form ax² + bx + c = 0.
- To determine the nature of the roots, we can use the discriminant (D), which is calculated as D = b² - 4ac.
- For this equation, a = 13, b = 5, and c = -2. Plugging in these values gives D = 5² - 4(13)(-2) = 25 + 104 = 129.
- Since the discriminant is positive (D > 0), it indicates that the roots are real and distinct.
Q17: From a thoroughly mixed deck of 52 playing cards, what is the probability of drawing a red queen?
(a) 1/13
(b) 1/26
(c) 4/13
(d) 1/4
 View Answer
View Answer 
Ans: (b)
- The total number of cards in a standard deck is 52.
- There are 2 red queens in the deck: the queen of hearts and the queen of diamonds.
- The probability of drawing a red queen is calculated as the number of favorable outcomes (2) divided by the total outcomes (52).
- This gives us a probability of 2/52, which simplifies to 1/26.
Q18: A cylinder is formed by joining the breadths of a rectangular sheet of dimensions 56 cm × 22 cm. Find its curved surface area.
(a) 1432 cm2
(b) 1442 cm2
(c) 1234 cm2
(d) 1232 cm2
 View Answer
View Answer 
Ans: (d)
CSA of the cone = Area of the rectangle = 56 × 22 = 1232 cm2
Q19: If Sn denotes the sum of the first n terms in an Arithmetic Progression and S1 : S4 = 1 : 10 then the ratio of first term to fourth term is:
(a) 1 : 3
(b) 2 : 3
(c) 1 : 4
(d) 1 : 5
 View Answer
View Answer 
Ans: (c)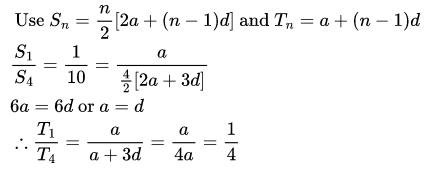
Q20: If two dice are rolled simultaneously, what is the probability that the total of the numbers on both dice is 10 or less?
(a) 11/12
(b) 1/12
(c) 7/12
(d) 1/9
 View Answer
View Answer 
Ans: (a)
- When rolling two dice, the possible outcomes range from 2 (1+1) to 12 (6+6).
- The total number of outcomes when rolling two dice is 36 (6 sides on the first die multiplied by 6 sides on the second die).
- The sums that are less than or equal to 10 include all combinations except for the sums of 11 and 12.
- There are 33 outcomes that result in a sum of 10 or less, leading to a probability of 33/36, which simplifies to 11/12.
Q21: The midpoint P of line segment joining the points A(-10, 4) and B(-2, 0) lies on the line segment joining the points C(-9, -4) and D(-4, 6). Find the ratio in which P divides CD.
(a) 1:4
(b) 2:3
(c) 4:1
(d) 3:2
 View Answer
View Answer 
Ans: (d)
- To find the midpoint P of line segment AB, use the formula: P = ((x1 + x2)/2, (y1 + y2)/2). Here, A(-10, 4) and B(-2, 0) give P = ((-10 - 2)/2, (4 + 0)/2) = (-6, 2).
- Next, we need to determine how P divides the line segment CD. The coordinates of C and D are C(-9, -4) and D(-4, 6).
- Using the section formula, if P divides CD in the ratio m:n, then P = ((mx2 + nx1)/(m+n), (my2 + ny1)/(m+n)). Setting this equal to P(-6, 2) allows us to solve for the ratio.
- After calculations, we find that P divides CD in the ratio 3:2.
Q22: A point moves such that its distance from the point (p, 0) is always three times its distance from the y-axis. Find its locus.
(a) 15x2 − y2 + 2px = p2
(b) 15x2 + y2 + 2px = p2
(c) 15x2 − y2 + 2px = p2
(d) 15x2 − y2 − 2px = p2
 View Answer
View Answer 
Ans: (c)
Let the point be P (x, y)
Its distance from (p, 0)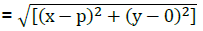 Its distance from the axis of y will be x
Its distance from the axis of y will be x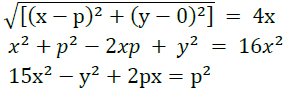
Q23: Study the bi-directional chart given below and answer the questions. The chart below represents the number of clients attended by Tom and Jack from January till June.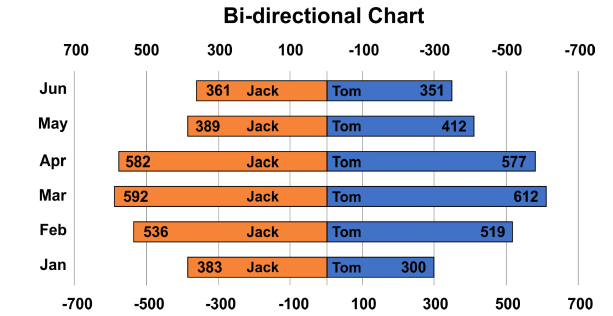
If 20% of Tom’s clients agreed to purchase the product in January, find the number of clients who didn’t agree.
(a) 30
(b) 60
(c) 120
(d) 240
 View Answer
View Answer 
Ans: (d)
80% of 300 = 240
Q24: Louis, Harvey, Mike and Pearson start running around a circular track simultaneously. If they complete one round in 15, 10, 12 and 18 minutes respectively, after how much time will they next meet at the starting point? Choose the right answer from the given options.
(a) 160
(b) 200
(c) 190
(d) 180
 View Answer
View Answer 
Ans: (d)
The time interval for them to meet at the starting point for the next time = LCM (10, 15, 12,18) = 180 minutes
Q25: If the 5th and 17th terms of an A.P. are 46 and 130, respectively, then find its 14th term.
(a) 116
(b) 109
(c) 123
(d) 95
 View Answer
View Answer 
Ans: (b)
- In an Arithmetic Progression (A.P.), the nth term can be expressed as: a + (n-1)d, where a is the first term and d is the common difference.
- Given the 5th term (a + 4d) is 46 and the 17th term (a + 16d) is 130.
- By setting up the equations: a + 4d = 46 and a + 16d = 130, we can solve for a and d.
- Subtracting the first equation from the second gives us 12d = 84, leading to d = 7. Substituting back, we find a = 46 - 28 = 18.
- Now, to find the 14th term: a + 13d = 18 + 13*7 = 18 + 91 = 109.
Q26: If the median of the distribution provided below is 35, what is the value of x? (Table-Based-Question)
(a) 8
(b) 10
(c) 12
(d) 7
 View Answer
View Answer 
Ans: (b)
- The median is the middle value of a data set when arranged in order. In this case, we know the median is 35.
- To find the value of x, we need to analyze the frequencies associated with the class intervals.
- Given the options, we can determine that the correct frequency that allows the median to be 35 is 10.
- Thus, the value of x that satisfies this condition is 10.
Q27: Simplify: (sin A + cos A) / (sin A - cos A) + (sin A - cos A) / (sin A + cos A) is equal to
(a) 2 / (2sin² A - cos² A)
(b) 1 / (2sin² A - cos² A)
(c) 0
(d) 4 / (2sin² A - cos² A)
 View Answer
View Answer 
Ans: (a)
- To simplify the expression, we can find a common denominator, which is (sin A - cos A)(sin A + cos A).
- After combining the fractions, we can simplify the numerator and denominator.
- Upon simplification, we find that the result is equal to 2 / (2sin² A - cos² A).
- This shows that the correct answer is option (a).
Q28: Which of the following statements is false?
(a) The rational form of 17.6 is 53/3.
(b) 0.423442344423... is a rational number.
(c) The fractional form of 16.29 is 19/1.
(d) √25 + √64 is a rational number.
 View Answer
View Answer 
Ans: (b)
- The statement that 0.423442344423... is a rational number is incorrect because it is a non-terminating, repeating decimal. Rational numbers can be expressed as a fraction of two integers, and this number cannot be simplified into such a form.
- In contrast, the other statements are true: 17.6 can be expressed as 53/3, 16.29 as 19/1, and the sum of √25 (5) and √64 (8) is 13, which is also a rational number.
Q29: Which of the following choices depicts the equation of the line shown in the graph?
(a) x + 2y - 6 = 0
(b) 2x + y - 5 = 0
(c) x - 2y + 7 = 0
(d) 3x - y + 6 = 0
 View Answer
View Answer 
Ans: (a)
- The equation of a line can be represented in the form of Ax + By + C = 0.
- To determine which equation matches the line in the graph, we can check the intercepts and slope of each option.
- After analyzing, we find that option (a) x + 2y - 6 = 0 correctly represents the line shown in the graph.
- Thus, the correct answer is option (a).
Q30: What value of 'p' will result in the system of equations having no solution? The equations are: px + 3y = p and 12x + y = p.
(a) 36
(b) 15
(c) 12
(d) 40
 View Answer
View Answer 
Ans: (a)
- For a system of equations to have no solution, the lines represented by the equations must be parallel. This occurs when the ratios of the coefficients of x and y are equal, but the constant terms are not.
- In this case, we can set up the ratios from the equations: p/3 = 12/1. Solving this gives p = 36.
- Thus, when p equals 36, the two lines will be parallel, leading to no intersection point, which means no solution.
- Therefore, the correct value of p that results in no solution is 36.
Q31: Two similar triangles ΔDRED and ΔDSKY have their areas in the ratio of 16:49. If the perimeter of ΔDSKY is 21 cm and the lengths of two sides of ΔDRED are 3 cm and 5 cm, what is the length of its third side?
(a) 4 cm
(b) 13 cm
(c) 15 cm
(d) 7 cm
 View Answer
View Answer 
Ans: (a)
- The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Here, the area ratio is 16:49, which means the ratio of the sides is √16:√49 = 4:7.
- The perimeter of ΔDSKY is 21 cm, so the corresponding perimeter of ΔDRED can be calculated using the side ratio. If we let the perimeter of ΔDRED be x, then 4/7 = x/21, leading to x = 12 cm.
- Now, the perimeter of ΔDRED is the sum of its sides: 3 cm + 5 cm + third side = 12 cm.
- Thus, the third side = 12 cm - (3 cm + 5 cm) = 12 cm - 8 cm = 4 cm.
Q32: If (x – 2) and (x - 1/2) are both factors of the polynomial px² + 5x + r, what is the value of p?
(a) 3/4 r
(b) 2r
(c) r/2
(d) r
 View Answer
View Answer 
Ans: (d)
- To determine the value of p, we can use the fact that if (x – 2) and (x - 1/2) are factors, then substituting these values into the polynomial should yield zero.
- Substituting x = 2 into the polynomial gives us the equation: p(2)² + 5(2) + r = 0.
- Substituting x = 1/2 gives us another equation: p(1/2)² + 5(1/2) + r = 0.
- Solving these equations simultaneously will show that p = r.
Q33: Find p such that  has equal roots with opposite signs.
has equal roots with opposite signs.
(a) 1
(b) 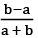 (c)
(c) 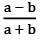 (d)
(d) 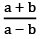
 View Answer
View Answer 
Ans: (c)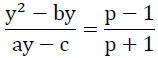 (p+1)y2−(p+1)by=(p−1)ay−c(p−1)
(p+1)y2−(p+1)by=(p−1)ay−c(p−1)
(p+1)y2−y[(p+1)b+(p−1)a]+c(p−1)=0
The coefficient of y must equate to 0.
[(p+1)b+(p−1)a]=0
pb+b+pa−a=0
p(a+b)=a−b
Q34: The third term of an A.P. is 21, and the seventh term is 37; find the sum of 17 terms.
(a) 918
(b) 1683
(c) 1530
(d) 765
 View Answer
View Answer 
Ans: (d)
a + 2d = 21 and a + 6d = 37
So, a = 13 and d = 4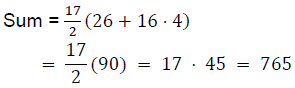
Q35: If sin(120° − α) = sin(120° − β) , 0 < α , β < π then find the relation between α and β.
(a) α < β
(b) α = β
(c) α + β = 60°
(d) Both (b) and (c)
 View Answer
View Answer 
Ans: (d)
If sin sin A =sin sin B, where A = 120° −α and B = 120°−β
A = B or A = π − B ,i.e.,A + B = π
120° −𝛼 = 120°−𝛽 𝑜𝑟,120° −𝛼 + 120° − 𝛽 = 180°
α = β or α+β= 60°
Everyday Mathematics
Q36: A factory produces on average 4500 items per month for the first 4 months. How many items must it produce on average per month over the next 8 months to average 4800 items per month over the whole year?
(a) 5100
(b) 4600
(c) 4950
(d) 4710
 View Answer
View Answer 
Ans: (c)
- To find the total items needed for the year, multiply the desired average (4800) by 12 months, which equals 57600 items.
- For the first 4 months, the factory produces 4500 items each month, totaling 18000 items.
- Subtract the total produced in the first 4 months from the yearly total: 57600 - 18000 = 39600 items needed for the next 8 months.
- To find the average per month for the next 8 months, divide 39600 by 8, which equals 4950 items.
Q37: If we purchase 2 tickets from station A to station B and 3 tickets from station A to C, the total cost is ₹795. However, if we buy 3 tickets from A to B and 5 tickets from A to C, the total comes to ₹1300. What are the respective fares from A to B and from A to C?
(a) ₹85, ₹312
(b) ₹75, ₹215
(c) ₹65, ₹115
(d) ₹95, ₹125
 View Answer
View Answer 
Ans: (b)
- Let the fare from A to B be represented as x and from A to C as y.
- From the first scenario: 2x + 3y = 795.
- From the second scenario: 3x + 5y = 1300.
- By solving these two equations, we find that x = 75 and y = 215.
- Thus, the fares from A to B and A to C are ₹75 and ₹215, respectively.
Q38: In a certain factory, each day the expected number of accidents is related to the number of overtime hours by a linear equation. Suppose that on one day there were 1000 overtime hours logged and8 accidents reported, and on another day there were400 overtime hours logged and 5 accidents. What are the expected numbers of accidents when no overtime hours are logged?
(a) 2
(b) 3
(c) 4
(d) 5
 View Answer
View Answer 
Ans: (b)
Let y be the no. of accidents, x is overtime hours, then y = ax + b where a and b are constants.
Substituting the values:
1000a + b = 8 and 400a + b = 5
We get a = 1/200 and b=3
For x = 0, y = 3.
Q39: A car travels from city A to city B at a constant speed. If its speed is increased by 12 km/h, it would have taken one hour less to cover the distance. It would have taken an additional 45 minutes less if the speed is further increased by 12 km/h. What is the distance between the cities?
(a) 540 km
(b) 504 km
(c) 405 km
(d) 450 km
 View Answer
View Answer 
Ans: (b)
- Let the original speed be x km/h and the distance be d km.
- From the problem, we know that increasing the speed by 12 km/h reduces the time by 1 hour, and increasing it by another 12 km/h (total increase of 24 km/h) reduces the time by an additional 45 minutes (or 0.75 hours).
- Using the formula: time = distance/speed, we can set up equations based on the information given.
- After solving these equations, we find that the distance d equals 504 km.
Q40: A person invested ₹2600 at 4%, 6%, and 8% per annum at simple interest. At the end of the year, he received the same interest from all three rates. How much was invested at 6%?
(a) ₹200
(b) ₹600
(c) ₹800
(d) ₹1200
 View Answer
View Answer 
Ans: (c)
- The total investment is ₹2600, and the interest earned from each rate is the same.
- Let the amount invested at 6% be x. Then, the amounts invested at 4% and 8% would be ₹2600 - x.
- The interest from each investment can be calculated using the formula: Interest = Principal × Rate × Time.
- Setting up the equations for the interest earned at each rate and solving them leads to the conclusion that the amount invested at 6% is ₹800.
Q41: 10 women can finish a task in 7 days, while 10 children require 14 days to complete the same task. How many days will it take for 5 women and 10 children to finish the work?
(a) 3
(b) 5
(c) 7
(d) 9
 View Answer
View Answer 
Ans: (c)
- First, calculate the total work done by women and children in terms of "work units".
- 10 women complete the work in 7 days, so their work rate is 10/7 work units per day.
- 10 children finish the work in 14 days, giving them a work rate of 10/14 work units per day.
- Now, find the combined work rate of 5 women and 10 children, which is (5 * 10/7) + (10 * 10/14).
- After calculating, you will find that they can complete the work in 7 days.
Q42: A cube with a side length of 3 cm has a weight of 12 kg. What would be the weight of a similar cube made of the same material with a side length of 12 cm?
(a) 768 kg
(b) 678 kg
(c) 964 kg
(d) 864 kg
 View Answer
View Answer 
Ans: (a)
- The weight of a cube is related to the volume of the cube, which is calculated as side length cubed (side³).
- For the first cube, the volume is 3 cm x 3 cm x 3 cm = 27 cm³, and it weighs 12 kg.
- The second cube has a side length of 12 cm, so its volume is 12 cm x 12 cm x 12 cm = 1728 cm³.
- Since the cubes are similar and made of the same material, the weight ratio is the same as the volume ratio. The weight of the second cube is calculated as follows: (1728 cm³ / 27 cm³) x 12 kg = 768 kg.
Q43: A solution of salt and water has a salt concentration of 42% by weight. If 25 kg of water evaporates and the resulting solution has a salt concentration of 56%, what was the original weight of the solution?
(a) 120 kg
(b) 100 kg
(c) 98 kg
(d) 123 kg
 View Answer
View Answer 
Ans: (b)
- Let the original weight of the solution be x kg. Since it contains 42% salt, the weight of salt in the solution is 0.42x kg.
- After 25 kg of water evaporates, the new weight of the solution becomes (x - 25) kg.
- The weight of salt remains the same, but now it constitutes 56% of the new solution, so we can set up the equation: 0.42x = 0.56(x - 25).
- Solving this equation gives us x = 100 kg, which is the original quantity of the solution.
Q44: Two tanks have equal capacity. The first tank measures 15 cm × 12 cm × 8 cm. The second tank features a square base with a depth of 10 cm. What is the length of the side of the square base?
(a) 12 cm
(b) 6 cm
(c) 8 cm
(d) 10 cm
 View Answer
View Answer 
Ans: (a)
- To find the side of the square base, we first calculate the volume of the first tank: Volume = length × width × height = 15 cm × 12 cm × 8 cm = 1440 cm³.
- The second tank has a volume given by the formula for a square base: Volume = side² × height. Here, the height is 10 cm.
- Setting the volumes equal: side² × 10 cm = 1440 cm³. Solving for side² gives side² = 1440 cm³ / 10 cm = 144 cm².
- Taking the square root, we find side = √144 cm² = 12 cm.
Q45: Rohan’s father has set up a plan to settle a debt of ₹3600 through 40 yearly payments that follow an arithmetic progression (A.P.). After 30 payments were made, his father passed away, leaving one-third of the debt still owed. What is the amount of the 10th installment?
(a) ₹35
(b) ₹59
(c) ₹65
(d) ₹69
 View Answer
View Answer 
Ans: (d)
- The total debt is ₹3600, and one-third of it is unpaid after 30 installments, which means ₹1200 is still owed.
- This indicates that ₹2400 has been paid through the 30 installments.
- Since there are 40 installments, the total amount paid can be expressed as the sum of an arithmetic series.
- Using the formula for the sum of an A.P., we can find the value of the 10th installment, which turns out to be ₹69.
Achievers Section
Q46: Examine the statements below and choose the accurate option.
(a) Both Statement I and Statement II are true.
(b) Both Statement I and Statement II are false.
(c) Statement I is true, but Statement II is false.
(d) Statement I is false, but Statement II is true.
 View Answer
View Answer 
Ans: (d)
- Statement I: The equation x² - x + 1 = 0 has roots that are not real because the discriminant (b² - 4ac) is negative (1 - 4 < 0).
- Statement II: The equation x² - 5x + 5 = 0 has real and distinct roots since its discriminant (25 - 20 = 5) is positive.
- Thus, Statement I is false and Statement II is true.
- Therefore, the correct answer is (d).
Q47: The integers 1, 2, …, 40 are written on a blackboard. The following operation is then repeated 39 times: In each repet it ion, any two numbers, say a and b, current ly on the blackboard are erased and a new number a + b – 1 is written. What will be the number left on the board at the end?
(a) 820
(b) 821
(c) 781
(d) 819
 View Answer
View Answer 
Ans: (c)
Total sum of the numbers written on the blackboard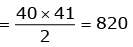 When two numbers ‘a’ and ‘b’ are erased and replaced by a new number a + b – 1, the total sum of the numbers written on the blackboard is reduced by 1.
When two numbers ‘a’ and ‘b’ are erased and replaced by a new number a + b – 1, the total sum of the numbers written on the blackboard is reduced by 1.
Since, this operation is repeated 39 times, therefore, the total sum of the numbers will be reduced by 1 × 39 = 39.
Therefore, after 39 operations there will be only 1 number that will be left on the blackboard and that will be 820 – 39 = 781.
Q48: V₁, V₂, V₃, and V₄ represent the volumes of four cubes with side lengths of x cm, 2x cm, 3x cm, and 4x cm, respectively. The following statements about these volumes are provided:
(1) V₁ + V₂ + 2V₃ < V₄
(2) V₁ + 4V₂ + V₃ < V₄
(3) 2(V₁ + V₃) + V₂ = V₄.
Which of the statements is accurate?
(a) (1) and (2) only
(b) (2) and (3) only
(c) (1) and (3) only
(d) (1), (2), and (3)
 View Answer
View Answer 
Ans: (d)
- To find the volumes, we calculate: V₁ = x³, V₂ = (2x)³ = 8x³, V₃ = (3x)³ = 27x³, and V₄ = (4x)³ = 64x³.
- Now, we evaluate the statements: (1) V₁ + V₂ + 2V₃ = x³ + 8x³ + 54x³ = 63x³ < 64x³ = V₄, which is true.
- (2) V₁ + 4V₂ + V₃ = x³ + 32x³ + 27x³ = 60x³ < 64x³ = V₄, which is also true.
- (3) 2(V₁ + V₃) + V₂ = 2(x³ + 27x³) + 8x³ = 62x³ = V₄, which is true as well.
- Since all statements are correct, the answer is (1), (2), and (3).
Q49: The number of common terms in the two sequences 17, 21, 25,…, 417 and 16, 21, 26,…, 466 is
(a) 78
(b) 19
(c) 20
(d) 77
 View Answer
View Answer 
Ans: (c)
Total number of terms in the sequence 17, 21, 25 …
417 is equal to 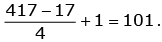 Total number of terms in the sequence 16, 21, 26 …
Total number of terms in the sequence 16, 21, 26 …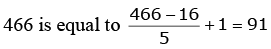
nth term of the first sequence = 4n + 13. mth term of the second sequence = 5m + 11.
As per the information given in the question 4n + 13= 5m + 11 ⇒ 5m – 4n = 2.
Possible integral values of n that satisfy 5m = 2 + 4nare (2, 7, 12 … 97)
Q50: Which of the following steps in the construction process is incorrect when drawing a tangent to a circle with a radius of 6 cm and forming a 30° angle with a line through the center?
Step I: Draw a circle with a radius of 6 cm and label its center as O. Mark a point P on the circumference of the circle.
Step II: Draw a line through the center O and the point P.
Step III: From point O, draw an angle of 30° with the line OP using a protractor.
Step IV: Draw a perpendicular line from point A (on OP) to meet the angle, ensuring it forms a tangent to the circle.
(a) Both Step I and Step IV
(b) Only Step III
(c) Both Step III and Step IV
(d) Only Step I
 View Answer
View Answer 
Ans: (a)
- The incorrect steps in the construction are identified as Step I and Step IV.
- In Step I, the radius should be 6 cm, not 3 cm as stated.
- In Step IV, the perpendicular from A to OP should be correctly drawn to ensure the tangent is accurate.
- Thus, both these steps do not align with the requirements for constructing the tangent correctly.
|
70 videos|242 docs|187 tests
|
FAQs on Mathematics Olympiad Model Test Papers - 2 - Olympiad Preparation for Class 10
| 1. What are the key topics covered in the Class 10 Mathematics Olympiad Model Test Papers? |  |
| 2. How can I prepare effectively for the Mathematics Olympiad exam? |  |
| 3. What is the importance of Logical Reasoning in the Mathematics Olympiad? |  |
| 4. Are the model test papers similar to the actual Olympiad exam format? |  |
| 5. What resources can I use to practice for the Achievers Section of the Mathematics Olympiad? |  |















