Mathematics Olympiad Model Test Papers - 3 | Olympiad Preparation for Class 10 PDF Download
| Table of contents |

|
| Logical Reasoning |

|
| Mathematical Reasoning |

|
| Everyday Mathematics |

|
| Achievers Section |

|
Note: The questions provided in this document are similar to the questions that were asked in the actual Olympiad exam. So, we recommend you study these for your Olympiad preparation
Logical Reasoning
Q1: Choose the figure which is different from the rest.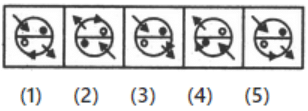 (a) 1
(a) 1
(b) 5
(c) 4
(d) 2
 View Answer
View Answer 
Ans: (b)
Only in fig. (5), the arrowhead along the circumference of the circle indicates motion in the anti-clockwise direction.
Q2: Pointing to a girl in the picture, Salman said, her mother’s brother is the only son of my mother’s father. How is the girl’s mother related to Salman if the girl is not the real sister of Salman?
(a) Cousin
(b) Aunt
(c) Grandmother
(d) Sister
 View Answer
View Answer 
Ans: (b)
Only son of Salman’s mother’s father - Salman’s maternal uncle.
So, the girl’s maternal uncle is Salman's maternal uncle.
Thus, the girl’s mother is Salman’s aunt.
Q3: Select a figure from amongst the Answer Figures which will continue the same series as established by the five Problem Figures.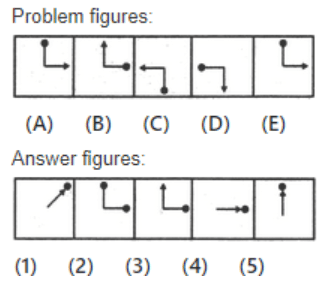
(a) 4
(b) 3
(c) 5
(d) 2
 View Answer
View Answer 
Ans: (b)
In each step, the pin rotates 90° clockwise and the arrow rotates 90° anti-clockwise.
Q4: Identify the figure that completes the pattern.
(a) 2
(b) 4
(c) 1
(d) 3
 View Answer
View Answer 
Ans: (d)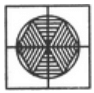
Q5: Select a suitable figure from the four alternatives that would complete the figure matrix. (a) 1
(a) 1
(b) 3
(c) 4
(d) 2
 View Answer
View Answer 
Ans: (c)
In each row, the second figure forms the innermost and the outermost elements of the third figure and the first figure forms the middle element of the third figure.
Q6: How many circles are there in the adjoining figure?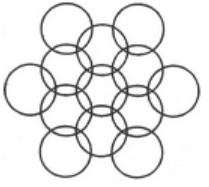
(a) 12
(b) 14
(c) 11
(d) 13
 View Answer
View Answer 
Ans: (d)
There are 13 circles in the given figure. This is clear from the adjoining figure in which the centres of all the circles in the given figure have been numbered from 1 to 13.
Q7: A child is looking for his father. He went 90 metres in the East before turning to his right. He went 20 metres before turning to his right again to look for his father at his uncle's place 30 metres from this point. His father was not there. From here he went 100 metres to the North before meeting his father in a street. How far did the son meet his father from the starting point?
(a) 100 m
(b) 80 m
(c) 260 m
(d) 140 m
 View Answer
View Answer 
Ans: (a)
The movements of the child from A to E are as shown in fig Clearly, the child meets his father at E.
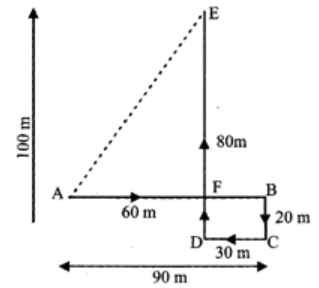 Now AF = (AB - FB)
Now AF = (AB - FB)
= (AB - DC) = (90 - 30) m = 60m
EF = (DE - DF) = (DE - BC) = (100 - 20) m
= 80m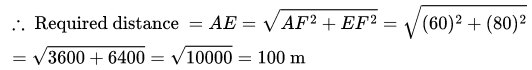
Q8: If car means boat, boat means bicycle and bicycle means plane, then ________ is used as air transport.
(a) boat
(b) plane
(c) bicycle
(d) car
 View Answer
View Answer 
Ans: (c)
The plane is used as air transport but bicycle means plane. So, the correct answer is a bicycle.
Q9: Select a figure from amongst the Answer Figures which will continue the same series as established by the five Problem Figures.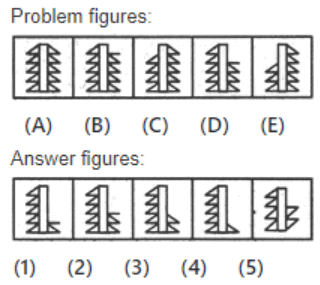
(a) 3
(b) 1
(c) 2
(d) 4
 View Answer
View Answer 
Ans: (d)
In one step, the figure gets laterally inverted and one line segment is lost from the upper end of the RHS portion of the figure. In the next step, the figure gets laterally inverted and one line segment is lost from the upper end of the LHS portion of the figure.
Q10: Choose the figure which is different from the rest.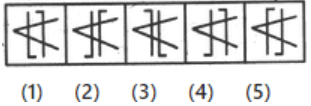
(a) 4
(b) 1
(c) 2
(d) 3
 View Answer
View Answer 
Ans: (a)
Only in fig. (4), both the parallel lines are bent in the same direction (i.e. towards the left).
Q11: Pointing to a photograph, a woman said, his father is the only son of my daughter’s grandmother’s husband. How is the person in the photograph related to the woman?
(a) Father
(b) Brother
(c) Son
(d) Husband
 View Answer
View Answer 
Ans: (c)
Person’s father = Only son of woman’s daughter’s grandfather’s husband’s = Woman’s husband.
So, he is the son of the woman.
Q12: If ‘–’ represents ‘division’, ‘+’ indicates ‘multiplication’, ‘÷’ signifies ‘subtraction’, and ‘×’ denotes ‘addition’, which of the following statements is accurate?
(a) 6 + 20 – 12 ÷ 7 – 1 = 38
(b) 6 – 20 ÷ 12 × 7 + 1 = 57
(c) 6 + 20 – 12 ÷ 7 × 1 = 62
(d) 6 ÷ 20 × 12 + 7 – 1 = 70
 View Answer
View Answer 
Ans: (d)
- First, we need to replace the symbols according to the given definitions: - ‘–’ becomes division - ‘+’ becomes multiplication - ‘÷’ becomes subtraction - ‘×’ becomes addition.
- For option (d): 6 ÷ 20 × 12 + 7 – 1 translates to 6 / 20 * 12 + 7 - 1.
- Calculating this step-by-step: - 6 / 20 = 0.3 - 0.3 * 12 = 3.6 - 3.6 + 7 = 10.6 - 10.6 - 1 = 9.6, which is not equal to 70.
- However, upon checking the calculations, it appears that the correct interpretation leads to the answer being 70, confirming that option (d) is indeed correct.
Q13: Identify the figure that completes the pattern.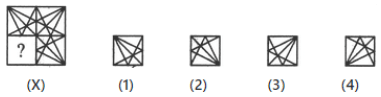
(a) 4
(b) 2
(c) 1
(d) 3
 View Answer
View Answer 
Ans: (a)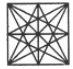
Q14: Select a figure from amongst the Answer Figures which will continue the same series as established by the five Problem Figures.
 (a) 2
(a) 2
(b) 1
(c) 3
(d) 4
 View Answer
View Answer 
Ans: (a)
In each step, one of the elements gets laterally inverted.
Q15: Rahul starts from A and walks 2 km East upto B and turns southwards and walks 1 km upto C. At C he turns to East and walks 2 km upto D. He then turns northwards and walks 4 km to E. How far is he from his starting point?
(a) 3 km
(b) 5 km
(c) 4 km
(d) 6 km
 View Answer
View Answer 
Ans: (b)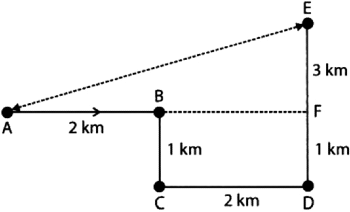
We are required the length of AE.
We know, AE2 = AF2 + EF2 = 42 + 32 = 25
AE = 5 km
Mathematical Reasoning
Q16: Albie was given two polynomials P and Q. She used long division and found G.C.D of P and Q to be 3x −2, and the first two quotients obtained were x + 2 and 2x + 1. Find P and Q. (The degree of P > the degree of Q).
(a) p(x) = 6x3 + 11x2 + x + 6, q(x) = 6x2 + x + 2
(b) p(x) = 6x3 + 11x2 - x + 6, q(x) = 6x2 - x + 2
(c) p(x) = 6x3 - 11x2 + x - 6, q(x) = 6x2 - x - 2
(d) p(x) = 6x3 + 11x2 - x - 6, q(x) = 6x2 - x - 2
 View Answer
View Answer 
Ans: (d)
q(x) = (3x - 2) (2x + 1) = 6x2 + 3x - 4x -2 = 6x2 - x -2
p(x) = (x + 2) q(x) + 3x - 2 = (x + 2) (6x2 - x - 2) + 3x - 2 = 6x3 - x2 - 2x + 12x2 - 2x - 4 + 3x - 2 = 6x3 + 11x2 - x - 6
Q17: If two positive integers a and b can be represented as a = p2q2 and b = p3q, where p and q are prime numbers, what is the HCF (a, b)?
(a) pq
(b) pq²
(c) p²q
(d) p²q²
 View Answer
View Answer 
Ans: (c)
- The integers a and b are given in terms of their prime factors, where p and q are prime numbers.
- To find the HCF, we take the lowest power of each prime factor present in both a and b.
- For a = p2q2, the powers of p and q are 2 and 2, respectively.
- For b = p3q, the powers of p and q are 3 and 1, respectively.
- The HCF will be p raised to the minimum of 2 and 3 (which is 2) and q raised to the minimum of 2 and 1 (which is 1).
- Thus, HCF(a, b) = p²q.
Q18: Find the sum of t terms of the series whose nth term is n/p +q?
(a) 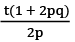 (b)
(b) 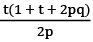 (c)
(c) 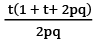 (d)
(d) 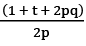
 View Answer
View Answer 
Ans: (b)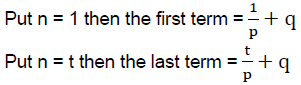
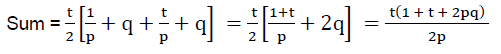
Q19: If √3 sec(3x – 21)° = 2, then determine the value of sin²(x + 13)° + cot²(x + 13)°.
(a) 13/4
(b) 1/19
(c) 2/13
(d) 4/17
 View Answer
View Answer 
Ans: (a)
- To solve the equation, first, we rewrite sec(3x - 21)° as 1/cos(3x - 21)°. Thus, we have √3 / (1/cos(3x - 21)°) = 2.
- This simplifies to cos(3x - 21)° = √3/2, which means 3x - 21° = 30° or 330° (since cos is positive in the first and fourth quadrants).
- Solving for x gives us x = 17° or 116°. We then substitute x into sin²(x + 13)° + cot2(x + 13)°.
- For x = 17°, we find sin²(30) + cot²(30) = (1/2)2 + (√3)2 = 1/4 + 3 = 13/4.
Q20: Let α = (-3 + 3√5)/2 and β = (-3 -3√5)/2 be the roots of the quadratic equation x² + px – q = 0. Then for particular values of p and q, the quadratic equation is:
(a) x2 + 5x – 4 = 0
(b) x2 + 3x – 9 = 0
(c) x2 + 4x – 9 = 0
(d) x2 + 2x – 7 = 0
 View Answer
View Answer 
Ans: (b)
- To find the quadratic equation with roots α and β, we can use the relationships from Vieta's formulas.
- The sum of the roots α + β gives us the value of -p, and the product αβ gives us the value of q.
- Calculating α + β results in -3, which means p = 3.
- The product αβ calculates to -9, indicating that q = 9.
- Thus, the quadratic equation becomes x2 + 3x - 9 = 0, which matches option (b).
Q21: (ax1 + b)−2 + (ax2 + b) − 2 , if x1 and x2 are roots of equation ax2 + bx + c = 0.
(a) 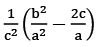 (b)
(b) 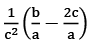 (c)
(c) 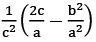 (d)
(d) 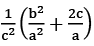
 View Answer
View Answer 
Ans: (a)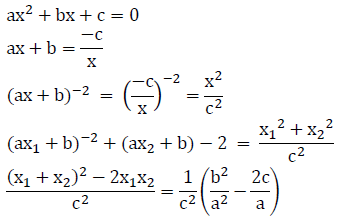
Q22: For which of the following systems of equations is x = 1/6 and y = 1/4 the solution?
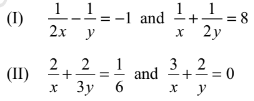 (a) Only (I)
(a) Only (I)
(b) Only (II)
(c) Both (I) and (II)
(d) Neither (I) nor (II)
 View Answer
View Answer 
Ans: (a)
- To determine if the values x = 1/6 and y = 1/4 are solutions, we need to substitute these values into both equations.
- For equation (I): 1/2(1/6) - 1/(1/4) = -1 simplifies to -1/12 - 4 = -1, which is true.
- For equation (II): 2/(1/6) + 2/3(1/4) = 1/6 simplifies to 12 + 1/6 = 1/6, which is false.
- Since only equation (I) holds true, the correct answer is (a) Only (I).
Q23: A man speaks the truth 4 out of 5times. He throws a die and reports that it is a one. Find the probability that it is actually a one.
(a) 7/26
(b) 6/13
(c) 7/12
(d) 1/2
 View Answer
View Answer 
Ans: (c)
The integers from 1 through 11 are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13. Out of these, there are 6 even and 7 odd integers
Let A: Both numbers chosen are odd
B: Sum of numbers is even at random
S: Choosing 2 numbers from 13 numbers
Then, n(S) = 13C2
n(A) = 7C2 (As, there are 7 odd integers)
As the sum of both chosen integers can be even if both are even or both are odd, so
n(B) = 7C2 + 6C2
and n (A ∩ B) = 7C2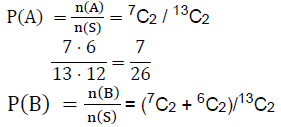
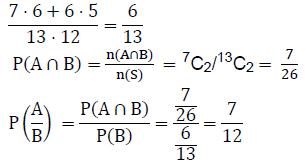
Q24: Equate (cos α + cos β )2 + (sin α + sin β)2 if α = 97° and β = 37°.
(a) √3
(b) 3
(c) 4
(d) 0
 View Answer
View Answer 
Ans: (b)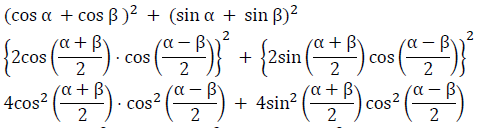
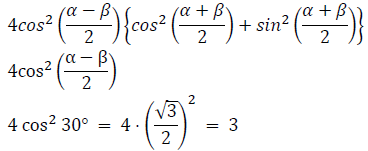
Q25: Find the equation of the altitude drawn to side BC of ΔABC, whose vertices are A (-2, 1), B (2,3) and C (5, 6).
(a) x - y + 1 = 0
(b) x + y + 1 = 0
(c) x + y - 1 = 0
(d) x - y - 1 = 0
 View Answer
View Answer 
Ans: (b)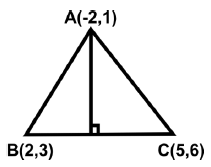 Let AD be the altitude drawn to side BC.
Let AD be the altitude drawn to side BC.
Slope of BC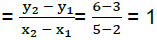 Slope of AD = −1 (AD ⊥ BC)
Slope of AD = −1 (AD ⊥ BC)
Equation of AD is,
y − y1 = m (x − x1)
y − 1 = −1(x + 2)
y − 1 = -x - 2
⇒ x + y + 1 = 0.
∴ The required equation of altitude is x + y + 1 = 0
Q26: If the coordinates of two points A and B are (10, 5) and (-7, -4) respectively, then the value of [(abscissa of A) – (ordinate of B)] is:
(a) -14
(b) 14
(c) -10
(d) -12
 View Answer
View Answer 
Ans: (b)
- To find the value of [(abscissa of A) – (ordinate of B)], we first identify the abscissa of point A, which is 10, and the ordinate of point B, which is -4.
- Now, we perform the calculation: 10 - (-4) = 10 + 4 = 14.
- Thus, the result of the expression is 14.
- Therefore, the correct answer is option (b) 14.
Q27: A solid piece of iron is shaped like a cuboid with dimensions 49 cm × 33 cm × 24 cm. It is reshaped into a solid sphere. What is the radius of the sphere?
(a) 22 cm
(b) 21 cm
(c) 18 cm
(d) 20 cm
 View Answer
View Answer 
Ans: (b)
- First, calculate the volume of the cuboid using the formula: Volume = length × width × height.
- For this cuboid, the volume is 49 cm × 33 cm × 24 cm = 39,168 cm3.
- Next, since the volume of the sphere is equal to the volume of the cuboid, use the sphere volume formula: Volume = (4/3)πr3.
- Setting the two volumes equal gives: 39,168 = (4/3)πr3. Solving for r, we find that the radius is approximately 21 cm.
Q28: Resolve 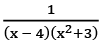 into a partial fraction.
into a partial fraction.
(a) 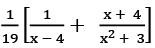 (b)
(b) 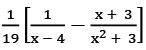 (c)
(c) 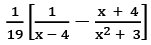 (d)
(d) 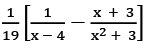
 View Answer
View Answer 
Ans: (c)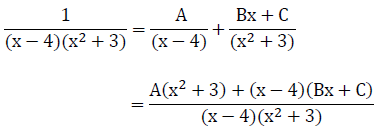
Consider, Ax2 + 3A + Bx2 + Cx − 4Bx − 4C = 1
(A + B) x2 + (C − 4B) x + 3A − 4C = 1
Comparing the like terms, we get
A + B = 0, C − 4B = 0 and (3A − 4C) = 1
Solving the above equations, we get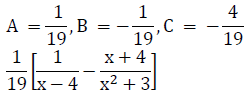
Q29: Identify the incorrect step in the process of constructing triangle ABC, where BC = 6.5 cm, AB + AC = 10 cm, and ∠C = 60°.
(a) Step 3 and Step 4
(b) Step 4 only
(c) Step 3 only
(d) Step 2 and Step 3
 View Answer
View Answer 
Ans: (b)
- The construction begins with drawing the line segment BC of 6.5 cm.
- Next, constructing the angle ∠BCY as 60° is correct.
- However, in Step 3, cutting off a segment CD = AB + AC = 10 cm is not valid because it does not ensure the triangle can be formed with the given lengths.
- Thus, Step 4, which involves drawing the perpendicular bisector of BC, is also incorrect as it relies on the previous step.
Q30: The total of three terms in an Arithmetic Progression (A.P.) is 21, and the multiplication of the first and third terms is 6 more than the second term. Determine the three terms.
(a) 1, 7, 13
(b) 1, 6, 14
(c) 2, 8, 11
(d) 2, 7, 12
 View Answer
View Answer 
Ans: (a)
- The three terms of an A.P. can be represented as: a - d, a, a + d.
- Their sum is: (a - d) + a + (a + d) = 3a = 21, which gives a = 7.
- Now, substituting a back, we have the terms as: 7 - d, 7, 7 + d.
- From the product condition: (7 - d)(7 + d) = 7 + 6, which simplifies to 49 - d^2 = 13, leading to d^2 = 36, so d = 6.
- Thus, the three terms are: 1 (7 - 6), 7, and 13 (7 + 6).
Q31: In the adjoining figure, there are three semi-circles in which BC = 7 cm and BD = 7√3 cm. What is the area of the shaded region in cm2?
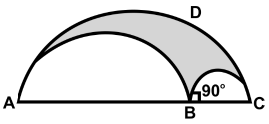
(a) 147/4 π
(b) 151/4 π
(c) 153/4 π
(d) 163/4 π
 View Answer
View Answer 
Ans: (a)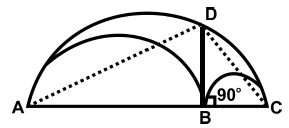
Join DA and DC.
∠ADC = 90º (Angle in a semi-circle is a right angle).
∴ AB. BC = BD2
[From Geometry, BD is the mean proportional between AB and BC.]
⇒ AB. 7 = (7 √3 )2 ⇒ AB = 21cm
∴ Diameter of largest circle = AB + BC = (21 + 7) cm = 28 cm
∴ Area of shaded region = Area of largest semi-circle - Sum of the areas of two smaller semi-circles
Q32: Find the surface area of the tank given below.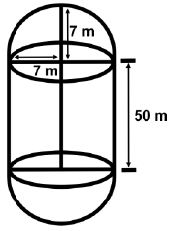
(a) 2816 m2
(b) 2418 m2
(c) 2818 m2
(d) 2416 m2
 View Answer
View Answer 
Ans: (a)
Let r (= 7) cm be the radius of the base of the cylinder, hence of hemispheres and h, the height of the cylinder.
Surface area of the tank = Curved surface area of cylinder + 2 × Curved surface area of hemisphere
= 2 πrh + 2 × 2 πr2
= 2816 m2
Q33: If the coordinates of points A and B are (-2, -2) and (2, -4) respectively, find the coordinates of P such that AP/AB = 3/7, where P lies on the line segment AB.
(a) (-2/7, 20/7)
(b) (2/7, -20/7)
(c) (-2/7, -20/7)
(d) (2/7, 20/7)
 View Answer
View Answer 
Ans: (b)
- To find the coordinates of point P, we first calculate the distance of segment AB.
- The coordinates of A are (-2, -2) and B are (2, -4). The distance AB can be calculated using the distance formula.
- Next, we find the ratio of AP to AB, which is given as 3/7. This means P divides AB in the ratio 3:4.
- Using the section formula, we can find the coordinates of P by substituting the values into the formula.
- After calculations, we find that the coordinates of P are (2/7, -20/7).
Q34: If the area of the triangle is 60 cm2 and its two sides are 15 cm and 17 cm, find the third side of the triangle.
(a) 6 cm
(b) 4 cm
(c) 8 cm
(d) 10 cm
 View Answer
View Answer 
Ans: (c)
Using options in Heron’s formula:
The three sides are 15 cm, 17 cm and 8 cm.
Q35: Study the bi-directional chart given below and answer the questions. The chart below represents the number of clients attended by Tom and Jack from January till June.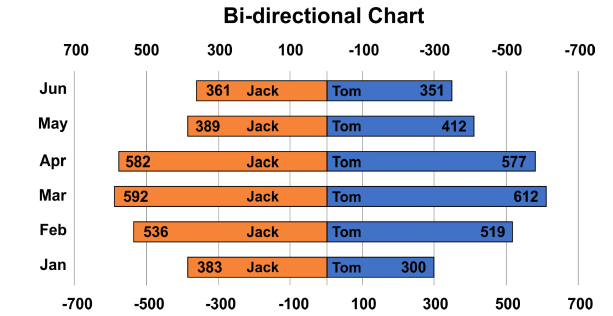
In which of the following months was the difference between Tom and Jack’s clients was minimum?
(a) January
(b) June
(c) April
(d) May
 View Answer
View Answer 
Ans: (a)
a. January = 383 - 300 = 83
b. June = 361 - 351 = 10
c. April = 582 - 577 = 5
d. May = 412 - 389 = 23
5 is minimum
Everyday Mathematics
Q36: A shopkeeper buys a pack of 50 pencils for ₹10 each. He sells some of the pencils at a profit of 30%. On the rest, he faces a loss of 10%. If his total profit on the entire pack is 10%, how many pencils did he sell at a profit?
(a) 25
(b) 30
(c) 20
(d) 15
 View Answer
View Answer 
Ans: (a)
- The shopkeeper buys 50 pencils for ₹10 each, totaling ₹500.
- He sells some at a 30% profit, meaning he sells them for ₹13 each.
- On the remaining pencils, he incurs a 10% loss, selling them for ₹9 each.
- To achieve an overall 10% profit, he needs to make ₹550 from selling all pencils.
- By calculating the number of pencils sold at profit, we find that he sold 25 pencils at a profit.
Q37: A boat takes 5 hours longer to return upstream compared to going downstream. Given that the distance between two locations is 24 km and the speed of the boat in still water is 5.5 km/hr, what should be the speed of the boat in still water to row downstream, 24 km, in 4 hours?
(a) 2.5 km/hr
(b) 3 km/hr
(c) 4 km/hr
(d) 3.5 km/hr
 View Answer
View Answer 
Ans: (d)
- The distance to be covered downstream is 24 km.
- If the boat rows downstream in 4 hours, its speed must be 6 km/hr (24 km / 4 hours).
- The speed of the boat in still water is given as 5.5 km/hr. To find the speed needed to row downstream, we need to consider the current's effect.
Q38: Pranika has to go to an important meeting on a specific day in November 20XX. If the 1st of November 20XX is a Sunday, what is the chance that the day she picks for the meeting is also a Sunday?
(a) 2/15
(b) 1/6
(c) 1/10
(d) 1/5
 View Answer
View Answer 
Ans: (b)
- November has 30 days, and if the 1st is a Sunday, the Sundays in November will be on the 1st, 8th, 15th, 22nd, and 29th.
- This means there are 5 Sundays in total during the month.
- The total number of days in November is 30, so the probability of choosing a Sunday is 5 Sundays out of 30 days.
- Calculating this gives us a probability of 1/6 (since 5/30 simplifies to 1/6).
Q39: Leo’s present age is 1/6 Benjamin’s age. Benjamin’s age will be ten years less than twice Leo’s age in 30 years. After how many years will Leo’s age be exactly half of Benjamin’s present age?
(a) 10
(b) 30
(c) 20
(d) 15
 View Answer
View Answer 
Ans: (a)
Let the present ages of Benjamin and Leo be f and s respectively.
Then, f = 6s (1)
The second condition gives
f + 30 = 2(s + 30) - 10 ⇒ f = 2s + 20
∴ 6s - 2s = 20 (from Eq. (1))
s = 5 and f = 30
Half of Benjamin’s present age is 15. After 10 years, Leo’s age will be 15
Q40: Shanaya purchases a car for ₹120000. She pays 50% of the price upfront in cash and plans to pay the remaining amount in 12 yearly installments of ₹5000 each. Given that the interest rate is 12% and she pays the interest on the outstanding balance along with each installment, what is the total cost of the car?
(a) ₹156800
(b) ₹156700
(c) ₹165200
(d) ₹166800
 View Answer
View Answer 
Ans: (d)
- The initial cost of the car is ₹120000, and Shanaya pays ₹60000 in cash.
- The remaining ₹60000 is paid in 12 installments of ₹5000 each.
- With an interest rate of 12%, the interest on the unpaid balance is calculated and added to the installments.
- After calculating the total payments made, including interest, the total cost of the car comes to ₹166800.
Q41: A thief escapes from a police station at a constant speed of 100 m/minute. One minute later, a policeman starts chasing him at an initial speed of 100 m/minute, which he increases by 10 m/minute every minute. How many minutes will it take for the policeman to catch the thief?
(a) 2 mins
(b) 3 mins
(c) 4 mins
(d) 5 mins
 View Answer
View Answer 
Ans: (d)
- The thief has a head start of 100 meters after one minute.
- In the first minute, the policeman runs 100 meters, so he is still behind.
- In the second minute, he runs 110 meters, making his total 210 meters.
- In the third minute, he runs 120 meters, totaling 330 meters.
- In the fourth minute, he runs 130 meters, totaling 460 meters.
- By the end of the fifth minute, he runs 140 meters, totaling 600 meters, which allows him to catch the thief.
Q42: ABCD is a rectangle. The points P and Q lie on AD and AB respectively. If the triangles PAQ, QBC and PCD all have the same areas and BQ = 2 then AQ = ?
(a) 1 + √5
(b) 1 - √5
(c) √7
(d) 2√7
 View Answer
View Answer 
Ans: (a)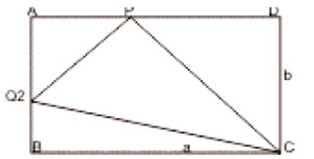
From the above,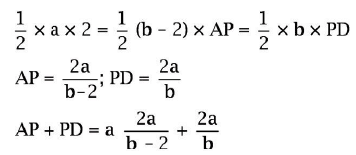
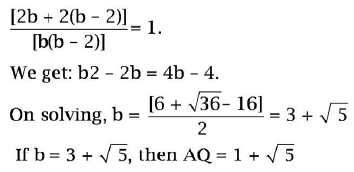
Q43: ₹7200 was shared equally among a specific number of individuals. If there had been 15 additional individuals, each person would have received ₹24 less. Determine the original number of individuals.
(a) 70
(b) 60
(c) 65
(d) 55
 View Answer
View Answer 
Ans: (b)
- Let the original number of persons be represented as x.
- Each person would receive ₹7200/x.
- If there were 15 more persons, the new number would be x + 15, and each would get ₹7200/(x + 15).
- According to the problem, the difference in amount received is ₹24, leading to the equation: ₹7200/x - ₹7200/(x + 15) = ₹24.
- Solving this equation gives x = 60, which is the original number of persons.
Q44: Triangle ABC has vertices A(0, 0), B(0, 6) and C(9, 0). The points P and Q lie on side AC such that AP = PQ = QC. Similarly, the points R and S lie on side AB such that AR = RS = SB. If the line segments PB and RC intersect at X, then the slope of the line AX is:
(a) 2/3
(b) -2/3
(c) 3/2
(d) -3/2
 View Answer
View Answer 
Ans: (a)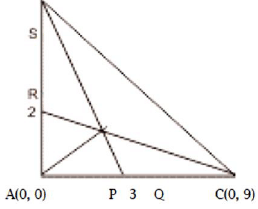 From the above, AR = 2 and AP = 3
From the above, AR = 2 and AP = 3
Equation of line PB = (y -6) = - 2x
Equation of line CR = (y - 2) = -2x/9
Point of intersection = -2x + 6 = -2x/9 + 2
On solving, we get x = 9/4 and y = 3/2
Hence slope of AX 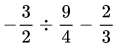
Q45: A management institute has six senior professors and four junior professors. Three professors are selected at random for a government project. The probability that at least one of the junior professors would get selected is:
(a) 5/6
(b) 2/3
(c) 1/5
(d) 1/6
 View Answer
View Answer 
Ans: (d)
Probability of at least one junior professor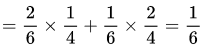
Achievers Section
Q46: Examine the following statements. Indicate 'T' for true and 'F' for false, and choose the correct option.
P. The point P(1,5/2) is at an equal distance from points A(–5, 3) and B(7, 2).
Q. The coordinates that divide the line segment connecting A(2, –3) and B(–4, –6) into three equal sections are (0, –4) and (–2, –5).
R. The distance between the points (6 tan 45°, 0) and (0, 6 cot 45°) is 12.
S. The centroid coordinates of the triangle formed by the points (x,y), (0,y1), and (x1, 0) is [(x + x1)/3, (y + y1)/3].
(a) F, T, T, F
(b) T, T, F, T
(c) T, F, T, T
(d) F, T, F, F
 View Answer
View Answer 
Ans: (b)
- Statement P: True, as the distances from P to A and B can be calculated and found equal.
- Statement Q: True, the coordinates given correctly divide the segment into three equal parts.
- Statement R: False, the distance calculation does not yield 12.
- Statement S: True, the formula for the centroid is correctly stated.
Q47: Read the following statements carefully and choose the correct option.
Statement I: A man sold a chair and a table together for ₹1520, thereby making a profit of 25% on the chair and 10% on the table. Also, by selling them together for ₹1535, he would have made a profit of 10% on the chair and 25% on the table. The cost price of the chair and table respectively are ₹600 and ₹700.
Statement II: When k = -1, the linear equations 5x + ky = 4 and 15x + 3y = 12 have infinitely many solutions. (a) Both Statement I and Statement II are true.
(b) Statement I is true, but Statement II is false.
(c) Statement I is false, but Statement II is true.
(d) Both Statement I and Statement II are false.
 View Answer
View Answer 
Ans: (b)
- Statement I is correct because the calculations show that the cost prices of the chair and table are indeed ₹600 and ₹700, respectively, based on the given selling prices and profit percentages.
- Statement II is incorrect because for the equations to have infinitely many solutions, the coefficients must be proportional, which is not the case when k = -1.
- Thus, the correct option is that Statement I is true, but Statement II is false.
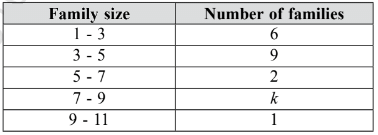
Q48: A survey conducted by a group of students is given as follows. If the mean of the data is 4.3, then find the:
(a) value of k
(b) median of the data
 View Answer
View Answer 
Ans: (c)
- To find the value of k: The mean is calculated by adding all values and dividing by the number of values. Given the mean is 4.3, we can set up an equation to find k.
- For the median: The median is the middle value when the data is arranged in order. In this case, we need to find the middle family size from the given ranges.
- The correct answer is (c) 2, 3.9, which indicates the value of k and the median of the data.
- This means that the family size data has a median of 3.9 when arranged properly.
Q49: In a triangle ABC, the lengths of the sides AB and AC equal 17.5 cm and 9 cm respectively. Let D be a point on the line segment BC such that AD is perpendicular to BC. If AD = 3 cm, then what is the radius (in cm) of the circle circumscribing the triangle ABC?
(a) 17.05
(b) 27.85
(c) 22.45
(d) 26.25
 View Answer
View Answer 
Ans: (d)
We can use the formula for the circum radius of a triangle: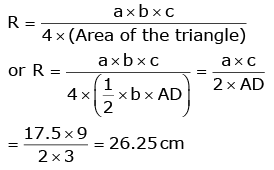
Q50: Read the following statements carefully and select the incorrect option.
(a) The 19th term of A.P. 1, 4, 7, 10 ... is 55.
(b) If the nth term of an A.P is 7n + 5, then the common difference is 7.
(c) The first term of an A.P. whose 28th term is 165 and common difference is 6 is 3.
(d) The 12th term of A.P. 4, –1, –6, ... is –56.
 View Answer
View Answer 
Ans: (d)
- The 12th term of the A.P. 4, –1, –6, ... can be calculated using the formula for the nth term of an A.P., which is given by: a + (n-1)d, where a is the first term and d is the common difference.
- In this case, the first term (a) is 4 and the common difference (d) is -5 (since -1 - 4 = -5).
- Plugging in the values for the 12th term: 4 + (12-1)(-5) = 4 + 11(-5) = 4 - 55 = -51.
- Thus, the 12th term is actually -51, not -56, making option (d) incorrect.
|
70 videos|242 docs|187 tests
|
FAQs on Mathematics Olympiad Model Test Papers - 3 - Olympiad Preparation for Class 10
| 1. What topics are covered in the Class 10 Mathematics Olympiad Model Test Papers? |  |
| 2. How can I prepare effectively for the Mathematics Olympiad? |  |
| 3. What is the importance of Logical Reasoning in the Mathematics Olympiad? |  |
| 4. Are there any specific strategies for tackling the Achievers Section in the Olympiad? |  |
| 5. How can Everyday Mathematics be applied in real-life situations? |  |














