Maths Olympiad Previous Year Paper -2 | Olympiad Preparation for Class 10 PDF Download
| Table of contents |

|
| Logical Reasoning |

|
| Mathematical Reasoning |

|
| Everyday Mathematics |

|
| Achievers Section |

|
Note: The questions provided in this document are similar to the questions that were asked in the actual Olympiad exam. So, we recommend you study these for your Olympiad preparation
Logical Reasoning
Q1: There is a specific connection between the numbers on both sides of the ::. Determine the relationship of the provided pair and find the unknown number.
12 : 159 : : 16 : ?
(a) 339
(b) 256
(c) 240
(d) 271
 View Answer
View Answer 
Ans: (b)
- To find the relationship, observe how 12 relates to 159. The calculation is: 12 x 13 + 3 = 159.
- Now apply the same logic to 16: 16 x 13 + 3 = 256.
- Thus, the missing number that corresponds to 16 is 256.
- This shows that the pattern involves multiplying by 13 and then adding 3.
Q2: Arrange the following words in the order they appear in a dictionary and select the correct sequence:
1. Remote,
2. Remedies,
3. Remainder,
4. Reminder,
5. Remove
(a) 2, 3, 4, 1, 5
(b) 3, 2, 4, 1, 5
(c) 3, 2, 4, 5, 1
(d) 2, 4, 3, 1, 5
 View Answer
View Answer 
Ans: (b)
- To determine the correct order, we look at the first letters of each word. All words start with 'R', so we check the second letters.
- The second letters are: e (Remote), e (Remedies), e (Remainder), i (Reminder), o (Remove). The order based on the second letters is: Remainder, Remedies, Remote, Reminder, Remove.
- Thus, the correct sequence is: 3 (Remainder), 2 (Remedies), 4 (Reminder), 1 (Remote), 5 (Remove).
- This corresponds to option (b) 3, 2, 4, 1, 5.
Q3: Select a figure from the options which will complete the given figure matrix. (a)
(a) 
(b) 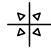
(c) 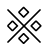
(d) 
 View Answer
View Answer 
Ans: (c)
In each row, the second figure is obtained by removing the outer layer of the first figure and the smaller shapes are replaced by new shapes. The third figure is obtained by rotating the second figure 45° clockwise
Q4: In the following question, there is a certain relationship between the two given numbers on one side of (: :) and one number is given on another side of (: :) where another number is to be found from the given alternatives, having the same relationship with this number as the numbers of the given pair bear. Choose the best alternatives.
25 : 625 : : 35 : ?
(a) 1575
(b) 1205
(c) 845
(d) 635
 View Answer
View Answer 
Ans: (d)
Q5: In the following question, one number is wrong in the series. Find out the number.
385, 462, 572, 396, 427, 671, 264
(a) 385
(b) 427
(c) 671
(d) 264
 View Answer
View Answer 
Ans: (b)
Q6: What will be the value of the expression if the numbers/digits ‘(6)’ and ‘(12)’ are interchanged?
164 ÷ 4 × 36 ÷ 12 × 5 + 6 + 9
(a) 1521
(b) 1251
(c) 1125
(d) 1152
 View Answer
View Answer 
Ans: (b)
The correct answer is Option 2 i.e. 1251
Given expression: 164 ÷ 4 × 36 ÷ 12 × 5 + 6 + 9
After interchanging numbers/digits, we get:
164 ÷ 4 × 36 ÷ 6 × 5 + 12 + 9
By using the rule of BODMAS, we get:
= (41 × 6 × 5 + 12 + 9)
= (1230 + 12 + 9)
= 1251
Q7: Select the correct combination of mathematical signs to sequentially replace the * signs and balance the given equation.
12 * 16 * 4 * 2 * 9 = 55
(a) ×, ÷, -, +
(b) ÷, ×, -, +
(c) ÷, +, -, ×
(d) ×, ÷, +, -
 View Answer
View Answer 
Ans: (a)
The correct answer is Option 1 i.e. ×, ÷, -, +
Given equation : 12 * 16 * 4 * 2 * 9 = 55
From option 1,
12 × 16 ÷ 4 - 2 + 9 = 48 - 2 + 9 = 55
Hence, the correct answer is ×, ÷, -, +.
Q8: If ‘+’ means ‘division’, ‘×’ means ‘minus’, “÷’ means ‘plus’ and ‘-‘ means ‘multiplied by’, then which of the following will be the value of the expression
99 ÷ 24 × 59 × 42 + 3 + 7 = ?
(a) 42
(b) 32
(c) 22
(d) 62
 View Answer
View Answer 
Ans: (d)
Given the equation: 99 ÷ 24 × 59 × 42 + 3 + 7 = ?
If ‘+’ means ‘division’, ‘×’ means ‘minus’, “÷’ means ‘plus’ and ‘-‘ means ‘multiplied
99 ÷ 24 × 59 × 42 + 3 + 7 = ?
= 99 + 24 - 59 - 42 ÷ 3 ÷ 7
= 99 + 24 - 59 - 2
= 62
Hence, 62 is the correct answer.
Q9: A square transparent sheet with a pattern and a dotted line on it is shown here. Select a figure from the options as to how the pattern would appear when the transparent sheet is folded along the dotted line.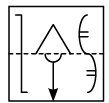 (a)
(a) 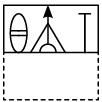
(b) 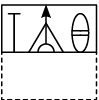
(c) 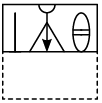
(d) 
 View Answer
View Answer 
Ans: (b)
Q10: A and B can do a piece of work in 72 days. B and C can do it in 120 days. A and C can do it in 90 days. In how many days all three together can do the work ?
(a) 80 days
(b) 100 days
(c) 60 days
(d) 150 days
 View Answer
View Answer 
Ans: (c)
Q11: A is as efficient as B and C together. Working together A and B can complete a work in 36 days and C alone can complete it in 60 days. A and C work together for 10 days. B alone will complete the remaining work in:
(a) 88 days
(b) 110 days
(c) 84 days
(d) 90 days
 View Answer
View Answer 
Ans: (b)
Q12: A alone can complete a work in 25 days and B alone can do the same work in 20 days. A started the work and after working 7 days B joined A to finish the remaining work. In how many days, the total work will be finished?
(a) 8 days
(b) 15 days
(c) 9 days
(d) 12 days
 View Answer
View Answer 
Ans: (b)
Q13: Which two numbers (NOT digits) should be interchanged to make the following equation correct?
28 ÷ 7 + 14 × 6 − 2 = 168
(a) 7 and 13
(b) 14 and 28
(c) 6 and 2
(d) 12 and 8
 View Answer
View Answer 
Ans: Given equation: 28 ÷ 7 + 14 × 6 − 2 = 168
Checking all the options one by one:
1. 6 and 2
28 ÷ 7 + 14 × 2 − 6 = 168
4 + 14 × 2 − 6 = 168
26 ≠ 168
26 is not equal to 168.
2. 14 and 28
14 ÷ 7 + 28 × 6 − 2 = 168
2 + 168 - 2 = 168
168 is equal to 168.
The equation is balanced. No need to check other options.
Hence, 14 and 28 is the correct answer.
Q14: Maya is the mother of Shruti. Varun and Kartik are brothers. Shruti is the sister of Varun and wife of Nakul. Which of the following statements are incorrect?
(a) Maya is the mother-in-law of Nakul.
(b) Shruti is the sister of Kartik.
(c) Kartik is the daughter-in-law of Nakul.
(d) Maya is the mother of Varun.
 View Answer
View Answer 
Ans: (c)
- The correct answer is (c) because Kartik is actually a brother, not a daughter-in-law. This makes the statement incorrect.
- Maya is indeed the mother of Shruti, making option (a) correct as she is the mother-in-law of Nakul.
- Shruti is the sister of Varun, but not of Kartik, which makes option (b) incorrect.
- Option (d) is correct since Maya is the mother of Varun as well.
Q15: Find the number of triangles formed in the given figure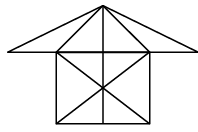 (a) 19
(a) 19
(b) 20
(c) 21
(d) More than 21
 View Answer
View Answer 
Ans: (d)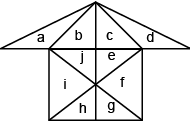 Triangles formed are : a, b, c, d, e, f, g, h, i, j, ab, bc, cd, je, bj, ce, hg, abc, bcd, ije, jef, fgh, ... i.e., more than 21.
Triangles formed are : a, b, c, d, e, f, g, h, i, j, ab, bc, cd, je, bj, ce, hg, abc, bcd, ije, jef, fgh, ... i.e., more than 21.
Mathematical Reasoning
Q16: Find the area of the triangle formed by the points (5, 3), (-9, -4) and (-3, -6).
(a) 18.5 units
(b) 19 units
(c) 18 units
(d) 19.5 units
 View Answer
View Answer 
Ans: (a)
0.5 x | {5. (-4) -(3. (-9) + (-9) (-6) - (-3) (-4) + (-3).3 - (-6) (5)} |
0.5 x 37 = 18.5 units
Q17: A and B being the fixed points (p, 0) and (-p, 0) respectively, obtain the equation giving the locus of P when PA2 - PB2 = 2K2.
(a) k2 − 2px = 0
(b) k2 − 2px = 0
(c) k2 + px = 0
(d) k + 2px = 0
 View Answer
View Answer 
Ans: (b)
Let point P be (x, y) while A and B are (p, 0) and (-q, 0)
Given relation is PA2 - PB2 = 2K2.
Upon using the distance formula
[(x-p)2+(y-0)2]-[(x+p)2+(y-0)2]=2K2
x2+p2-2xp + y2 - [x2+p2 + 2xp +y2] = 2K2
-4xp=2K2 =k2 + 2px = 0
Q18: Find the median to the side BC of the triangle whose vertices are A (−2, 1), B (2, 3) and C (4, 5).
(a) 3x − 5y + 11 = 0
(b) 3x + 5y + 11 = 0
(c) 3x − 5y - 11 = 0
(d) 3x + 5y - 11 = 0
 View Answer
View Answer 
Ans: (a)
Let E be the mid-point of side BC. 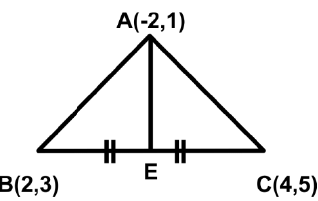
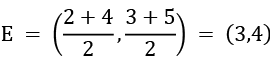
Equation of line AE is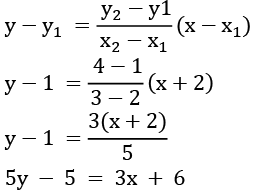
∴ The required equation of the median is 3x − 5y + 11 = 0.
Q19: What is the difference between the circumradius and inradius of a triangle whose sides are 3 cm, 4cm and 5 cm?
(a) 1 cm
(b) 2.5 cm
(c) 2 cm
(d) 1.5 cm
 View Answer
View Answer 
Ans: (d)
Inradius = 1 cm
Circumradius = 2.5 cm
Difference = 2.5 - 1 = 1.5 cm
Q20: In the triangle given below, find the length of side BC if the value of x is 50 cm.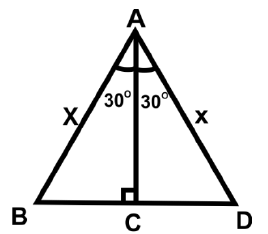 (a) 25 cm
(a) 25 cm
(b) 30 cm
(c) 22.5 cm
(d) 30.5 cm
 View Answer
View Answer 
Ans: (a)
In isosceles triangle ABC, BC/x = sin 30°
If x = 50 cm
So, BC = 50 sin 30° = 50 × 1/2 = 25 cm
Q21: Find the length of DB if AD is the angle bisector of ∠A and CB is 2 cm less than AB.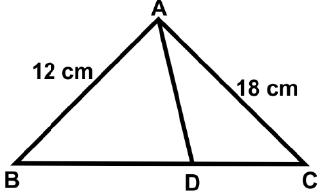 (a) 4 cm
(a) 4 cm
(b) 6 cm
(c) 10 cm
(d) 8 cm
 View Answer
View Answer 
Ans: (d)
AD is the angle bisector of ∠A
So, ∠BAD = ∠CAD
BD = 8 cm
Q22: In the given figure, PQ, PR and QR are the tangents to the circle with centre O. A, B and C are points of contact. If PQ = 12 cm, PR = 10 cm, and CR = 2 cm, then find the perimeter of the ∆PQR.
(a) 24 cm
(b) 28 cm
(c) 22 cm
(d) 26 cm
 View Answer
View Answer 
Ans: (b)
PQ = PA + AQ = 12 cm
PR = PC + CR = 10 cm
PC + 2 = 10 cm ⇒ PC = 8 cm
⇒ PA = 8 cm (∴ PA = PC)
⇒ AQ = BQ = 12 − 8 = 4 cm
Perimeter of DPQR = PQ + QR + RP = PA + AQ + BQ + BR + RC + CP
= 8 + 4 + 4 + 2 + 2 + 8 = 28 cm
Q23: How many common tangents are possible for two circles having a radius of 5 cm and 2 cm with a distance between their centres as 3 cm?
(a) 1
(b) 0
(c) 2
(d) 4
 View Answer
View Answer 
Ans: (a)
It will form two concentric circles with 1 possible common tangent.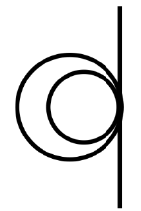
Q24: A two-digit number is 4 greater than 6 times the total of its digits. If you subtract 18 from this number, the digits will be reversed. What is the number?
(a) 36
(b) 64
(c) 25
(d) 30
 View Answer
View Answer 
Ans: (b)
- The two-digit number can be represented as 10a + b, where a is the tens digit and b is the units digit.
- According to the problem, the number is 4 more than 6 times the sum of its digits: 10a + b = 6(a + b) + 4.
- When 18 is subtracted from the number, the digits are reversed: 10a + b - 18 = 10b + a.
- Solving these equations leads to the conclusion that the number is 64.
Q25: A box holds 54 balls, which are either red, green, or black. The chance of randomly picking a red ball is 1/3, and the chance of picking a green ball is 4/9. How many black balls are in the box?
(a) 10
(b) 8
(c) 15
(d) 12
 View Answer
View Answer 
Ans: (d)
- The total number of balls is 54.
- The probability of selecting a red ball is 1/3, which means there are 18 red balls (54 * 1/3).
- The probability of selecting a green ball is 4/9, leading to 24 green balls (54 * 4/9).
- To find the number of black balls, subtract the red and green balls from the total: 54 - 18 - 24 = 12 black balls.
Q26: Find the volume of a cone whose base radius is 21 cm and the angle at its vertex is 90° (in cm3).
(a) 9602 cm3
(b) 9702 cm3
(c) 9404 cm3
(d) 9604 cm3
 View Answer
View Answer 
Ans: (b)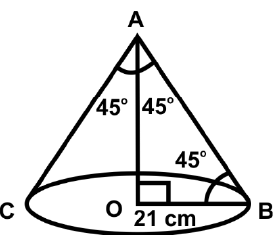 Given r = 21 cm and ∠BAC = 90°
Given r = 21 cm and ∠BAC = 90°
∠OAB = 45°
Height (h) = OA = 21 cm
Volume = 1/3 πr2h = 9702 cm3
Q27: Select the incorrect option:
(a) In a parallelogram, the sum of any two consecutive angles is 180°.
(b) In a triangle ABC, if median AD is extended to X such that AD = DX, then ABXC is a parallelogram.
(c) Both A and B
(d) Neither A nor B
 View Answer
View Answer 
Ans: (d)
- In a parallelogram, the property states that the sum of any two consecutive angles is indeed 180°.
- In triangle ABC, if median AD is extended to point X such that AD equals DX, then ABXC forms a parallelogram.
- Since both statements A and B are true, the correct answer is that neither A nor B is incorrect.
- Thus, the answer is (d) Neither A nor B.
Q28: The total of all terms in an arithmetic sequence with ten terms, excluding the first term, equals 99, and excluding the sixth term, equals 89. Determine the 8th term of the sequence, given that the sum of the first and fifth terms is 10.
(a) 15
(b) 25
(c) 18
(d) 10
 View Answer
View Answer 
Ans: (a)
- Let the first term be a and the common difference be d.
- The sum of the first ten terms is given by the formula: S = n/2 * (2a + (n-1)d).
- From the problem, we know that the sum excluding the first term (S - a) is 99, and excluding the sixth term (S - (a + 5d)) is 89.
- By solving these equations, we find that the 8th term, which is a + 7d, equals 15.
Q29: The curved surface area of a frustum of a cone whose slant height is equal to the sum of radii (R, r) of the circular ends of the frustum can be represented as:
(a) 2π (R + r)2
(b) π (R + r)2
(c) 3π (2R + r)2
(d) 4π (R + r)2
 View Answer
View Answer 
Ans: (b)
CSA = π l (R + r)and (l = R + r)
Q30: If the radius of the base of a cone is reduced to half while maintaining the same height, what is the ratio of the volume of the smaller cone to that of the original cone?
(a) 1 : 4
(b) 2 : 3
(c) 4 : 1
(d) 3 : 2
 View Answer
View Answer 
Ans: (a)
- The volume of a cone is calculated using the formula: V = (1/3)πr2h, where r is the radius and h is the height.
- If the radius is halved, the new radius becomes r/2. Plugging this into the volume formula gives V' = (1/3)π(r/2)2h = (1/3)π(r2/4)h = (1/4)(1/3)πr2h.
- This shows that the volume of the new cone is one-fourth of the original cone's volume.
- Thus, the ratio of the volume of the reduced cone to the original cone is 1:4.
Q31: In a cylindrical vessel of diameter 12 cm filled up with a sufficient quantity of water, a solid spherical ball of radius 6 cm is completely immersed. What is the increase in height of the water level?
(a)12 cm
(b) 8 cm
(c) 4 cm
(d) 2 cm
 View Answer
View Answer 
Ans: (b)
Let the height of the increased water level be h cm.
Then, Volume of water displaced = Volume of the sphere
⇒ πr2h = 4/3 πR3, (where, r = radius of cylinder, R = radius of sphere)
6 × 6 × h = 4/3 × 6 × 6 × 6
h = 8 cm
Q32: What will be the volume of a square pyramid whose base is 2 metres and height is 3 metres?
(a) 12 m3
(b) 4π m3
(c) 4 m3
(d) 2π m3
 View Answer
View Answer 
Ans: (c)
Q33: The length of the longest diagonal of a cuboid is 5√5 cm, and the length of one of the longest face diagonals is 10 cm. If the lengths of the edges are integers in cm, then find the volume of the cuboid (in cm3).
(a) 200
(b) 120
(c) 240
(d) 48
 View Answer
View Answer 
Ans: (c)
h = 5 cm
∴ Volume = lbh = 8 × 6 × 5 = 240 cm3
Q34: A man begins his employment with a specific monthly salary and receives a consistent annual increase. If his salary was ₹15,000 after 4 years and ₹18,000 after 10 years, what are his initial salary and annual increment, respectively?
(a) ₹11,000, ₹700
(b) ₹13,000, ₹500
(c) ₹13,000, ₹700
(d) ₹11,000, ₹500
 View Answer
View Answer 
Ans: (b)
- Let the initial salary be ₹x and the annual increment be ₹y.
- After 4 years, the salary is ₹15,000: x + 4y = 15,000.
- After 10 years, the salary is ₹18,000: x + 10y = 18,000.
- By solving these two equations, we find that the initial salary is ₹13,000 and the annual increment is ₹500.
Q35: Find the volume of the cylinder whose radius is 6 feet and height is 4 metres.
(a) 172π ft3
(b) 144π ft3
(c) 92π ft3
(d) 152π ft3
 View Answer
View Answer 
Ans: (b)
Everyday Mathematics
Q36: A train measuring 100 m in length takes 9 seconds to pass a person walking at 5 km/hr in the opposite direction. What is the speed of the train?
(a) 30 km/hr
(b) 45 km/hr
(c) 35 km/hr
(d) 50 km/hr
 View Answer
View Answer 
Ans: (b)
- To find the speed of the train, we first calculate the relative speed between the train and the man. Since they are moving in opposite directions, we add their speeds.
- The man walks at 5 km/hr, and we need to convert the train's length and crossing time into the same unit. The train is 100 m long and takes 9 seconds to cross.
- First, convert the train's length to kilometers: 100 m = 0.1 km. The time taken is 9 seconds, which is 9/3600 hours (since there are 3600 seconds in an hour).
- Now, the speed of the train relative to the man is calculated as: Speed = Distance / Time = 0.1 km / (9/3600) hr = 40 km/hr.
- Adding the man's speed: 40 km/hr + 5 km/hr = 45 km/hr. Thus, the speed of the train is 45 km/hr.
Q37: ₹9,000 was shared equally among a specific number of individuals. If there had been 20 additional individuals, each person would have received ₹160 less. What is the original number of individuals?
(a) 25
(b) 24
(c) 26
(d) 27
 View Answer
View Answer 
Ans: (a)
- Let the original number of persons be x. Then, each person receives ₹9000/x.
- If there are 20 more persons, the new number becomes x + 20, and each would get ₹9000/(x + 20).
- According to the problem, the difference in amount received is ₹160, leading to the equation: ₹9000/x - ₹9000/(x + 20) = ₹160.
- Solving this equation gives x = 25, which is the original number of persons.
Q38: A and B solved a quadratic equation. In the process, A incorrectly calculated the constant term and found the roots to be 5 and –3, while B incorrectly calculated the coefficient of x and found the roots to be 1 and –3. What are the correct roots of the equation?
(a) 1, 3
(b) –1, 3
(c) –1, –3
(d) 1, –1
 View Answer
View Answer 
Ans: (b)
- The roots found by A (5, –3) and B (1, –3) indicate that both made errors in their calculations.
- To find the correct roots, we can analyze the patterns in the mistakes made by A and B.
- Considering the nature of quadratic equations, the correct roots must be consistent with the errors made.
- After evaluating the possible roots, the correct roots of the equation are determined to be –1 and 3.
Q39: Two containers A and B have milk and water combined in the ratios of 5:2 and 8:5, respectively. Determine the ratio in which these mixtures should be combined to achieve a new mixture with milk and water in the ratio of 9:4.
(a) 7:2
(b) 5:7
(c) 3:5
(d) 4:9
 View Answer
View Answer 
Ans: (a)
- To find the required ratio, we first calculate the amount of milk and water in each mixture.
- In vessel A, for every 7 parts (5 milk + 2 water), there are 5 parts of milk and 2 parts of water.
- In vessel B, for every 13 parts (8 milk + 5 water), there are 8 parts of milk and 5 parts of water.
- We set up equations based on the desired ratio of 9:4 and solve for the mixing ratio, which results in 7:2.
Q40: There were 35 students residing in a hostel. With the addition of 7 new students, the daily mess expenses rose by ₹42, while the average cost per student decreased by ₹1. What was the initial expenditure of the mess?
(a) ₹421
(b) ₹422
(c) ₹420
(d) ₹430
 View Answer
View Answer 
Ans: (c)
- Let the original total expenditure of the mess be X.
- Initially, there were 35 students, so the average expenditure per student was X/35.
- After 7 new students joined, there were 42 students, and the new average expenditure became X/42.
- According to the problem, the increase in total expenses is ₹42, leading to the equation: X/42 = (X + 42)/42.
- Also, the average expenditure decreased by ₹1, giving us another equation: X/35 - X/42 = 1.
- Solving these equations, we find that the original expenditure X = ₹420.
Q41: 16 men can finish a task in 12 days, while 24 children can accomplish the same task in 18 days. If 12 men and 8 children begin the work, and after 8 days, 3 additional children join them, how many days will it take to finish the remaining work?
(a) 4
(b) 6
(c) 8
(d) 7
 View Answer
View Answer 
Ans: (a)
- First, calculate the total work in terms of man-days: 16 men can do the work in 12 days, so total work = 16 * 12 = 192 man-days.
- Next, find the work done by 12 men and 8 children in 8 days. 12 men do 12 * 8 = 96 man-days. 24 children can do the work in 18 days, so 8 children do (8/24) * 18 = 6 man-days in 8 days.
- Thus, total work done in 8 days = 96 + 6 = 102 man-days. Remaining work = 192 - 102 = 90 man-days.
- After 8 days, 3 more children join, making it 12 men and 11 children. They can do (12 + 11/3) = 12 + 3.67 = 15.67 man-days per day.
- Finally, to finish the remaining 90 man-days, it will take 90 / 15.67 ≈ 5.74 days, which rounds up to 6 days.
Q42: The maximum possible sphere is carved out of a cube of an edge of 14 cm. Find its surface area (in cm2).
(a) 616
(b) 256
(c) 444
(d) 546
 View Answer
View Answer 
Ans: (a)
Diameter of the sphere = the edge of the cube = 14 cm
⇒ 2r = 14 cm ⇒ r = 7 cm
Surface area = 4πr2 = 616 cm2
Q43: The difference between the curved surface area of a sphere of radius R and that of a cylinder of base radius r and height 2R can be represented as:
(a) 2π (R + r)2
(b) π (R + r)2
(c) 3π (2R + r)2
(d) 4π (R2 + Rr)
 View Answer
View Answer 
Ans: (d)
Q44: A sum is invested for 3 years, compounded annually at rates of 5%, 10%, and 20%. After these three years, the total amount is ₹16,632. What was the original investment amount?
(a) ₹12,000
(b) ₹11,000
(c) ₹15,000
(d) ₹9,000
 View Answer
View Answer 
Ans: (a)
Q45: A shopkeeper sells a pair of sunglasses with a profit margin of 25%. If he had purchased it for 25% less and sold it for ₹10 less, he would have made a profit of 40%. What is the cost price of the sunglasses?
(a) ₹25
(b) ₹50
(c) ₹60
(d) ₹75
 View Answer
View Answer 
Ans: (b)
- Let the cost price of the sunglasses be x.
- With a 25% profit, the selling price becomes 1.25x.
- If the cost price was 25% less, it would be 0.75x, and selling it for ₹10 less gives a selling price of 1.25x - 10.
- According to the problem, this selling price results in a 40% profit, which means it equals 1.4 * 0.75x.
- Setting up the equation: 1.25x - 10 = 1.4 * 0.75x leads to solving for x, which gives x = ₹50.
Achievers Section
Q46: Find the difference between the edge and height of a square pyramid whose volume is 16 m3 and height is 12 m.
(a) 11 m
(b) 2 m
(c) 10 m
(d) 8 m
 View Answer
View Answer 
Ans: (c)
Volume = 1/3 a2h
h = 12 m and a = 2 m
Difference = 12 - 2 = 10 m
Q47: The probability that a steam iron fails on first use is 0.20, if it doesn’t fail on first use, the probability that it lasts for one year is 0.90. What is the probability that a new steam iron will last for a year?
(a) 0.72
(b) 0.63
(c) 0.65
(d) 0.86
 View Answer
View Answer 
Ans: (a)
Probability that a steam iron for one year = (Probability that the iron doesn't fail) × (probability that it lasts for one year)
= (1 − 0.20) (0.90) = 0.90 × 0.99 = 0.720
Q48: Three parties are contesting in an election. The probability of their winning is 0.6,0.3,0.1 respectively. If party A wins, it introduces a new scheme with a probability of 0.7 and such probability for other parties is 0.6 and 0.5. With what probability a new scheme is certain to be introduced.
(a) 0.64
(b) 0.65
(c) 0.67
(d) 0.70
 View Answer
View Answer 
Ans: (b)
P(A) = 0.6, P(B) = 0.3, P(C) = 0.1
If N is for introducing new scheme, then
P(N∣A) = 0.7, P(N∣B) = 0.6, P(N∣C) = 0.5
Therefore,
P(N) = P(A) × P(N∣A) + P(B) × P(N∣B) + P(C) × P(N∣C)
= 0.6 × 0.7 + 0.3 × 0.6 + 0.1 × 0.5 = 0.65
Q49: A frog takes a jump forward with a probability of 0.3 and backward with a probability of 0.7. Find the probability that at the end of eleven jumps it is one step away from the starting position.
(a) 0.168
(b) 0.178
(c) o.198
(d) 0.188
 View Answer
View Answer 
Ans: (d)
Since the frog is one step away from the starting point that means either
Frog has taken 6 steps forward and 5 steps backward
Frog has taken 5 steps forward and 6 steps backward
Taking 1 jump forward as success and 1 jump backward as failure
P = probability of success = 0.3
Q = probability of failure = 0.7
Q = probability of failure = 0.7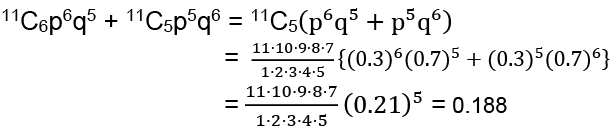
Q50: If tan θ = a sin φ/(1 - a cos φ) and tan φ = b sin θ/(1 - b cos θ), then find the value of a/b:
(a) sin θ/(1 - cos θ)
(b) sin θ/(1 - cos φ)
(c) sin φ/sin θ
(d) sin θ/sin φ
 View Answer
View Answer 
Ans: (d)
|
70 videos|242 docs|187 tests
|
FAQs on Maths Olympiad Previous Year Paper -2 - Olympiad Preparation for Class 10
| 1. What topics are typically covered in the Class 10 Maths Olympiad exam? |  |
| 2. How can I prepare effectively for the Class 10 Maths Olympiad? |  |
| 3. Are the questions in the Maths Olympiad exam difficult compared to regular school exams? |  |
| 4. What resources are recommended for studying for the Maths Olympiad? |  |
| 5. How is the scoring system structured in the Class 10 Maths Olympiad? |  |














