Worksheet Solutions: HCF & LCM | Mathematics for Class 5 PDF Download
Q1: Answer the following questions:
1. Write the first 3 multiples of 21.
Ans: The first three multiples of 21 are: 21, 42, 63.
2. Which of the following numbers are composite?
2, 7, 15, 27, 29, 37, 53, 69, 87.
Ans: The composite numbers from the given list are: 15, 27, 69, 87.
Q2: Write two prime numbers whose difference is 1.
Ans: There are no prime numbers whose difference is 1. The smallest gap between any two prime numbers is 2, known as twin primes (e.g., 11 and 13).
Q3: Write all composite numbers between 90 and 100.
Ans: The composite numbers between 90 and 100 are: 90, 91, 92, 93, 94, 95, 96, 98, 99.
Q4: Which of the following pairs are coprime?
1. 18 and 30
Ans: The greatest common divisor (GCD) of 18 and 30 is 6, so they are not coprime.
2. 35 and 52
Ans: The GCD of 35 and 52 is 1, so they are coprime.
Q5: Is it possible that a number is divisible by 8 but not divisible by 4?
Ans: No, it is not possible for a number to be divisible by 8 but not divisible by 4. If a number is divisible by 8, it must also be divisible by 4 because 8 is a multiple of 4.
Q6: Which of these numbers are divisible by 3 or 4 or both?
1. 87,342
Ans: 87,342 is divisible by 3 (sum of digits = 27, which is divisible by 3), but it is not divisible by 4 (last two digits 42 are divisible by 4).
2. 23,148
Ans: 23,148 is not divisible by 3 (sum of digits = 18, which is divisible by 3) but is divisible by 4 (last two digits 48 are divisible by 4).
Q7: Test the divisibility of the following numbers by 3:
1. 90,82,746
Ans: 90,82,746 is divisible by 3 (sum of digits = 36, which is divisible by 3).
2. 70,335
Ans: 70,335 is not divisible by 3 (sum of digits = 18, which is divisible by 3).
Q8: Test the divisibility of the following numbers by 5:
1. 2,01,234
Ans: 2,01,234 is divisible by 5 (the last digit is 4, not 0 or 5, so it is not divisible by 5).
2. 4,37,839
Ans: 4,37,839 is not divisible by 5 (the last digit is 9, not 0 or 5).
Q9: Test the divisibility of the following numbers by 9:
1. 3,478
Ans: 3,478 is not divisible by 9 (sum of digits = 22, which is not divisible by 9).
2. 8,74,512
Ans: 8,74,512 is divisible by 9 (sum of digits = 27, which is divisible by 9).
Q10: Test the divisibility of the following numbers by 11:
1. 1,00,01,001
Ans: 1,00,01,001 is divisible by 11 (alternating sum of digits from right to left = 1 - 0 + 0 - 0 + 1 - 0 + 0 - 0 + 1 = 3, which is not divisible by 11).
2. 5,335
Ans: 5,335 is not divisible by 11 (alternating sum of digits = 5 - 3 + 3 - 5 = 0, which is divisible by 11).
Q11: In each of the following numbers, replace * by the smallest number to make it divisible by 9:
1. 66784 *
Ans: To make a number divisible by 9, the sum of its digits must be divisible by 9.
For 66784*, the sum of the digits is 6 + 6 + 7 + 8 + 4 = 31. The smallest number to add to 31 to make it divisible by 9 is 4 (31 + 4 = 35). Therefore, replace * with 4.
2. 5321 * 43
Ans: To make a number divisible by 9, the sum of its digits must be divisible by 9.
For 5321*43, the sum of the digits is 5 + 3 + 2 + 1 + 4 + 3 = 18. Since 18 is already divisible by 9, the smallest number to replace * with is 0 (18 + 0 = 18).
Q12: Test the divisibility of the following numbers by 4:
1. 7,314
Ans: 7,314 is divisible by 4 (the last two digits, 14, are divisible by 4).
2. 9,31,105
Ans: 9,31,105 is not divisible by 4 (the last two digits, 05, are not divisible by 4).
Q13: Find the H.C.F. of:
1. 14 and 35
Ans: The highest common factor (H.C.F.) of 14 and 35 is 7.
2. 15 and 35
Ans: The H.C.F. of 15 and 35 is 5.
3. 30, 75 and 90
Ans: The H.C.F. of 30, 75, and 90 is 15.
4. 8 and 40
Ans: The H.C.F. of 8 and 40 is 8.
Q14: Find all the common factors of:
1. 16 and 40
Ans: The common factors of 16 and 40 are 1, 2, 4, 8.
2. 18 and 45
Ans: The common factors of 18 and 45 are 1, 3, 9.
3. 12 and 15
Ans: The common factors of 12 and 15 are 1, 3.
4. 52 and 117
Ans: The common factors of 52 and 117 are 1, 13.
Q15: Find the L.C.M. of the following numbers:
1. 5 and 8
Ans: The least common multiple (L.C.M.) of 5 and 8 is 40.
2. 4 and 9
Ans: The L.C.M. of 4 and 9 is 36.
3. 12 and 15
Ans: The L.C.M. of 12 and 15 is 60.
4. 26 and 15
Ans: The L.C.M. of 26 and 15 is 390.
5. 8, 10 and 12
Ans: The L.C.M. of 8, 10, and 12 is 120.
6. 6 and 10
Ans: The L.C.M. of 6 and 10 is 30.
7. 9 and 11
Ans: The L.C.M. of 9 and 11 is 99.
Q16: Write in the product form:
1. 24 × 52 × 32
Ans: 24 × 52 × 32
2. 65 × 26 × 32
Ans: 65 × 26 × 32
3. 67 × 105
Ans: 67 × 105
4. 48
Ans: 48
Q17: Fill the vacant circles in each of the following factor trees.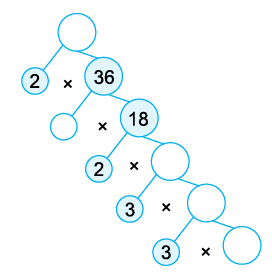 Ans: Starting with 2 and 36: 36 is factored into 2 and 18.
Ans: Starting with 2 and 36: 36 is factored into 2 and 18.
Next, 18 is broken down into 2 and 9: 9 should be factored into 3 and 3.
So, to complete the factor tree:
- The circle next to 18 should be filled with a 9.
- The two bottom circles next to the number 3 (from the 9 decomposition) should both be filled with 3, as 9 is broken down into 3 × 3.
Q18: Find the HCF of the following numbers by long division method:
1. 40, 75
Ans: HCF of 40 and 75
Divide 75 by 40, remainder = 35.
Divide 40 by 35, remainder = 5.
Divide 35 by 5, remainder = 0.
HCF = 5.
2. 24, 64
Ans: HCF of 24 and 64
Divide 64 by 24, remainder = 16.
Divide 24 by 16, remainder = 8.
Divide 16 by 8, remainder = 0.
HCF = 8.
3. 27, 45
Ans: HCF of 27 and 45
Divide 45 by 27, remainder = 18.
Divide 27 by 18, remainder = 9.
Divide 18 by 9, remainder = 0.
HCF = 9.
4. 81, 117
Ans: HCF of 81 and 117
Divide 117 by 81, remainder = 36.
Divide 81 by 36, remainder = 9.
Divide 36 by 9, remainder = 0.
HCF = 9.
5. 18, 45, 36
Ans: HCF of 18, 45, and 36
HCF of 18 and 45 is 9 (as found earlier).
HCF of 9 and 36: Divide 36 by 9, remainder = 0.
HCF = 9.
6. 54, 96, 120
Ans: HCF of 54, 96, and 120
HCF of 54 and 96:
Divide 96 by 54, remainder = 42.
Divide 54 by 42, remainder = 12.
Divide 42 by 12, remainder = 6.
Divide 12 by 6, remainder = 0.
HCF of 6 and 120:
Divide 120 by 6, remainder = 0.
HCF = 6.
7. 70, 98, 154
Ans: HCF of 70, 98, and 154
HCF of 70 and 98:
Divide 98 by 70, remainder = 28.
Divide 70 by 28, remainder = 14.
Divide 28 by 14, remainder = 0.
HCF of 14 and 154:
Divide 154 by 14, remainder = 0.
HCF = 14.
Q19: Find the L.C.M. by prime factorisation method:
1. 15 and 20
Ans: LCM of 15 and 20
15 = 3 × 5
20 = 22 × 5
LCM = 22 × 3 × 5 = 60
2. 24 and 36
Ans: LCM of 24 and 36
24 = 23 × 3
36 = 22 × 32
LCM = 23 × 32 = 72
3. 42 and 91
Ans: LCM of 42 and 91
42 = 2 × 3 × 7
91 = 7 × 13
LCM = 2 × 3 × 7 × 13 = 546
4. 50 and 105
Ans: LCM of 50 and 105
50 = 2 × 52
105 = 3 × 5 × 7
LCM = 2 × 3 × 52 × 7 = 1050
5. 4, 36 and 52
Ans: LCM of 4, 36, and 52
4 = 22
36 = 22 × 32
52 = 22 × 13
LCM = 22 × 32 × 13 = 468
6. 10, 35 and 40
Ans: LCM of 10, 35, and 40
10 = 2 × 5
35 = 5 × 7
40 = 23 × 5
LCM = 23 × 5 × 7 = 280
7. 12 and 18
Ans: LCM of 12 and 18
12 = 22 × 3
18 = 2 × 32
LCM = 22 × 32 = 36
Q20: Answer the following questions:
1. The HCF of two numbers is 19 and their LCM is 228. If one of the numbers is 57, find the other.
Ans: If the HCF of two numbers is 19 and their LCM is 228, and one of the numbers is 57, find the other:
Formula: Product of numbers = HCF × LCM
57 × x = 19 × 228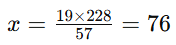
2. The product of two numbers is 25,024 and their H.C.F. is 8. Find their L.C.M.
Ans: The product of two numbers is 25,024 and their H.C.F. is 8. Find their L.C.M.:
Formula: HCF × LCM = Product of the numbers
8 × LCM = 25,024
LCM = 25,024/8 = 3128
|
98 videos|661 docs|47 tests
|






















