Differential Calculus Chapter Notes | Quantitative Aptitude for CA Foundation PDF Download
Chapter Overview
Introduction
Differentiation is a key operation in calculus, rooted in the concepts of limits and function continuity. It serves to express the rate of change in a function through the introduction of the derivative, which measures the small change in the dependent variable relative to a small change in the independent variable.
In essence, differentiation involves finding the derivative of a continuous function. This process is defined as the limit of the ratio of the change in the function to the change in the independent variable as the latter approaches zero.
Derivative of Differential Coefficient
Let y = f(x) be a function. If h (or x) be the small increment in x and the corresponding increment in y or f(x) be y = f(x+h) – f(x) then the derivative of f(x) is defined
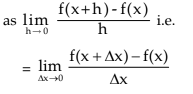
This is denoted as f’(x) or dy/ dx or d/dx f(x). The derivative of f(x) is also known as differential coefficient of f(x) with respect to x. This process of differentiation is called the first principle (or definition or abinitio) (Ab-initio).
Note: In the light of above discussion a function f (x) is said to differentiable at x = c if
exist which is called the differential coefficient of f(x) at x = c and is denoted by f ‘(c) or
.
We will now study this with an example.
Consider the function f(x) = x2 .
By definition
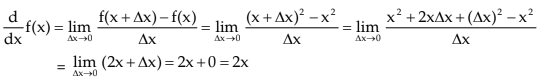
Thus, derivative of f(x) exists for all values of x and equals 2x at any point x.
Examples of differentiations from the 1st principle
i) f(x) = c, c being a constant.
Since c is constant we may write f(x+h) = c.
So f(x+h) – f(x) = 0
Hence 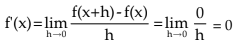
ii) Let f(x) = xn; then f(x+h) = (x+h)n
let x+h =t or h= t – x and as h0, tx

Hence 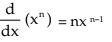
iii) f (x) = ex ∴ f(x + h) = ex+h
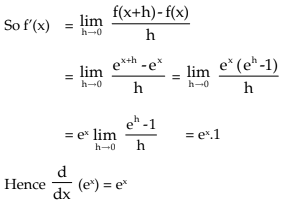
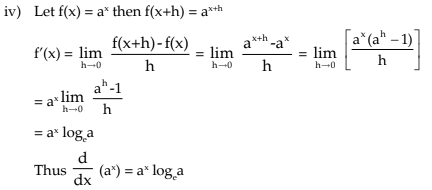

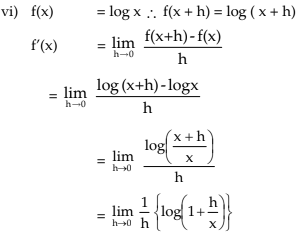

Some Standard Results (Formulas)
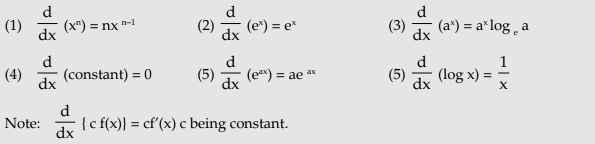
In brief we may write below the above functions and their derivatives:

We also tabulate the basic laws of differentiation.

It should be noted here even though in (ii), (iii), (iv) and (v) we have considered two functions f and g, it can be extended to more than two functions by taking two by two.
Example: Differentiate each of the following functions with respect to x:
(a) 3x2 + 5x –2
(b) ax + xa + aa
(c) 
(d) ex log x
(e) 2x x5
(f) x2 / ex
(g) ex / logx
(h) 2x . log x
(i) 2x / 3x3 +7
Solution:
(a) Let y = f(x) = 3x2 + 5x –2
= 3 × 2x + 5.1 – 0 = 6x + 5
(b) Let h(x) = a x + x a + a a
(h) Let h(x) = 2x . log x
The given function h(x) is appearing here as product of two functions
(i) Let
[Given function appears as the quotient of two functions]
f(x) = 2x and g(x) = 3x3 + 7
Derivative of Function of a Function
If y = f [h(x)] then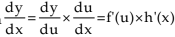 x where u = h(x)
x where u = h(x)Example: Differentiate log (1 + x2) wrt. x
Solution: Let y = log (1 + x2) = log t when t = 1 + x2
This is an example of derivative of function of a function and the rule is called Chain Rule.
Implicit Function
- A function written in the form f(x, y) = 0 is called an implicit function.
- For instance, the equation x²y² - 3xy + y = 0 is an example of an implicit function of x since y cannot be easily expressed as a function of x.
- To express y as an explicit function of x in order to find dy, we differentiate both sides of the equation with respect to x.
- In this process, we substitute dy/dx = y into the equation, which helps us simplify the differentiation.
- After performing the differentiation, we can solve for y' or the derivative of y.
- For implicit functions, if y is a differentiable function of x, there is no need to rearrange the resulting equation into a different form.
Example: Find dy / dx for x2y2 + 3xy + y = 0
Solution: x2y2 + 3xy + y = 0
Differentiating with respect to x we see
This is the procedure for differentiation of Implicit Function.
Parametric Equation
When both x and y are defined using a third variable, known as a parameter, the resulting equations are referred to as parametric equations.- For the parametric equations x = f(t) and y = h(t), the derivative dy/dx can be calculated using the formula: dy/dx = (dy/dt) / (dx/dt).
- For example, to find dy/dx when x = at3 and y = a/t3:
- dx/dt = 3at2
- dy/dt = -3a/t4
- This illustrates the method for differentiating parametric functions.
Logarithmic Differentiation
The technique of finding a derivative using logarithms at the beginning is known as logarithmic differentiation.- This method is particularly useful when the function to differentiate includes another function in an exponent or when it is a product of several functions.
Example: Differentiate xx w.r.t. x
Solution: let y = xx
Taking logarithm,
log y = x log x
Differentiating with respect to x,
This procedure is called logarithmic differentiation.
Some More Examples
(1) If 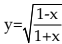 show that
show that 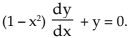
Solution: Taking logarithm, we may write log y = 1/2 {log (1 – x) – log (1 + x)}
Differentiating throughout we have
By cross–multiplication (1 – x2) dy / dx = – y
Transposing (1 – x2) dy / dx + y = 0.
(2) Differentiate the following w.r.t. x:
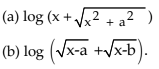
Solution:
(a)
=
(b) Let
(3) If xm yn = (x+y) m+n prove that dy/dx = y / x
Solution: xm yn = (x+y) m+n
Taking log on both sides
log xm yn = (m+n) log (x + y)
or m log x + n log y = ( m+n) log (x+y)
(4) If xy= ex–y prove that 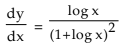
Solution: xy= ex–y
So y log x = (x – y) log e
or y log x = (x – y) ..............(a)
Differentiating w.r.t. x we get
Basic Idea About Higher Order Differentiation
Let y = f(x) = x4 + 5x3 + 2x2 + 9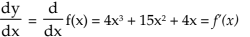
Since f(x) is a function of x it can be differentiated again.
Thus 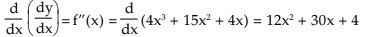
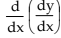 is written as d2y/dx2 (read as d square y by dx square) and is called the second derivative of y with respect to x while dy/dxis called the first derivative. Again the second derivative d d2 y here being a function of x can be differentiated again and
is written as d2y/dx2 (read as d square y by dx square) and is called the second derivative of y with respect to x while dy/dxis called the first derivative. Again the second derivative d d2 y here being a function of x can be differentiated again and 
= f'''(x) = 24x +30.
Example: If y = ae mx + be – mx prove that d2y/dx2 = m2y.
Solution: 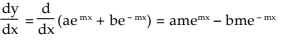
Geometric Interpretation of the Derivative
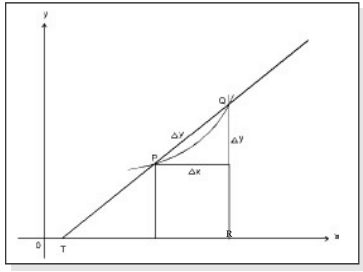
Let f(x) represent the curve in the fig. We take two adjacent pairs P and Q on the curve Let f(x) represent the curve in the fig. We take two adjacent points P and Q on the curve whose coordinates are (x, y) and (x + Δx, y+Δy) respectively. The slope of the chord TPQ is given by
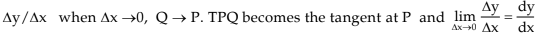
The derivative of f(x) at a point x represents the slope (or sometime called the gradient of the curve) of the tangent to the curve y = f(x) at the point x. If  exists for a particular point say x =a and f(a) is finite we say the function is differentiable at x = a and continuous at that point.
exists for a particular point say x =a and f(a) is finite we say the function is differentiable at x = a and continuous at that point.
Example: Find the gradient of the curve y = 3x2 – 5x + 4 at the point (1, 2).
Solution:
y = 3x2 – 5x + 4
∴ dx / dy = 6x – 5
so [dy /dx] x = 1 y = 2
= 6.1 –5 =6–5=1
Thus the gradient of the curve at (1, 2) is 1.
|
114 videos|164 docs|98 tests
|
FAQs on Differential Calculus Chapter Notes - Quantitative Aptitude for CA Foundation
| 1. What is the basic concept of limits in differential calculus? |  |
| 2. How do you find the derivative of a function using the definition? |  |
| 3. What are the different rules for differentiation? |  |
| 4. What is the significance of the first and second derivatives? |  |
| 5. How can one apply derivatives to solve real-world problems? |  |
|
114 videos|164 docs|98 tests
|

|
Explore Courses for CA Foundation exam
|

|
 exist which is called the differential coefficient of f(x) at x = c and is denoted by f ‘(c) or
exist which is called the differential coefficient of f(x) at x = c and is denoted by f ‘(c) or  .
.






 [Given function appears as the quotient of two functions]
[Given function appears as the quotient of two functions] 




























