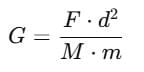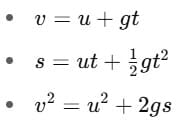Class 9 Science Chapter 9 Practice Question Answers - Gravitation
Gravitation is a fundamental concept that has been studied for centuries. It is a force that exists between any two objects in the universe, and it governs the motion of planets, stars, and galaxies. In the context of Class 9 Physics, the study of gravitation introduces students to the basic principles of the force, its effects on objects, and its application in various scenarios. Let us see some Numerical Practice Questions from this chapter.

Basic Formulae
1. Universal Law of Gravitation
Where:
F = Gravitational force between two bodies
G = Universal gravitational constant 6.67×10−11Nm2/kg2
M, m = Masses of two bodies
d = Distance between centres of the two bodies
2. Gravitational Constant
3. Force on an Object on Earth (Weight)
F = m ⋅ g
Where:
F = Force or weight
m = Mass of the object
g = Acceleration due to gravity (9.8 m/s2 on Earth)
4. Equations of Motion (for Free Fall)
(Here, u is initial velocity, v is final velocity, s is distance, t is time)
5. Weight of a Body
W = m ⋅ g
SI unit of weight is newton (N)
Q1. Let us find the force of attraction between two blocks lying 1m apart. Let the mass of each block be 40 kg.
Sol. Given:
Mass of each block = 40 kg
Distance between blocks, r =1 m
Gravitational constant, G = 6.674×10−11 Nm2/kg2
Formula:
 The formula for the gravitational force between two objects is:
The formula for the gravitational force between two objects is:
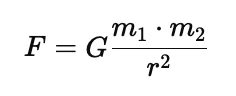
Where:
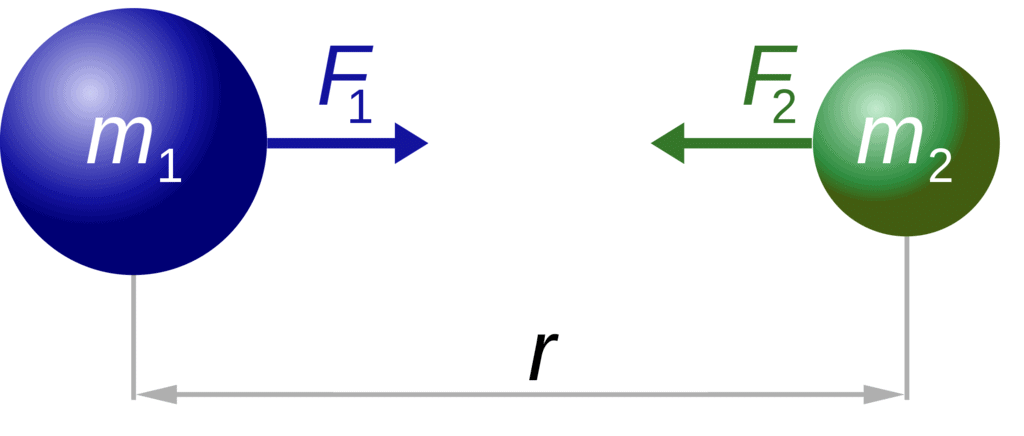
F is the gravitational force.
G is the universal gravitational constant (6.67430 x 10-11 N·m2/kg2).
m1 and m2 are the masses of the two objects.
r is the distance between the centres of the two objects.
Substitute the given values: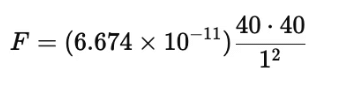
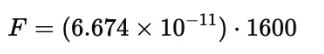
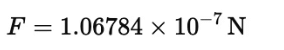
The force of attraction between the two blocks is 1.06784×10−7N.
Q2. The gravitational force between two objects is 49 N. How much distance between these objects must be decreased so that the force between them becomes double?
Sol. Step-1 : Here, F = 49 N
Let r = original distance between the objects.
m1and m2= masses of the objects
F = G m1 × m2/r² …(1)
Let the new distance be R, and then the force is 2F.
We get, 2F = G m1 × m2/R²…(2)
Dividing equation (2) by (1)
2 = r²/R²
R² = r²/2
R = r/√2
Hence decrease in distance = r-r/√2 = r (√2 - 1)/√2
Q3. Two bodies, A and B, having masses 2 kg and 4 kg respectively, are separated by 2m. Where should a body of mass 1 kg be placed so that the gravitational force on this body due to bodies A and B is zero?
Sol.
Given:
Mass of body A, m1 = 2 kg
Mass of body B, m2 = 4 kg
Distance between A and B = 2 m
Mass of body C, m = 1 kg

Let body C be placed at a distance x from A.
Then, AC = x and BC = (2 − x)
Since gravitational force on C due to A = gravitational force on C due to B:
F1 = F2
G × m1 × m / x² = G × m2 × m / (2 − x)²
⇒ m1 / x² = m2 / (2 − x)²
⇒ 2 / x² = 4 / (2 − x)²
⇒ 2x² = (2 − x)²
Taking the square root on both sides:
√2 × x = 2 − x
1.414x + x = 2
⇒ 2.414x = 2
⇒ x = 2 / 2.414 ≈ 0.83 m
Final Answer: The body should be placed at a distance of approximately 0.83 m from body A.
Q4. Calculate the force of gravitation due to a child of mass 25 kg on his fat mother of mass 75 kg if the distance between their centres is 1m from each other. Given G = (20/3) × 10-11 Nm2 kg-2.
Sol.Here m1 = 25 kg ; m2 = 75 kg ; d = 1 m ; G = 20/3 × 10-11 Nm2 kg-2
Using F = Gm1m2/d2
F = 20/3 x 10-11 x 75 x 25/ (1)2
F = 12,500 × 10-11
or F = 1.25 × 10-7N
Q5. A boy drops a stone from the edge of the roof. If it passes a window 2m high in 0.1s. How far is the roof above the top of the window?
Sol. Let a stone be dropped from the edge of the roof A. Let it pass over B with a velocity, say u. Consider motion BC.
u = ?, a = 9.8 ms-2; s = h = 2m ; t = 0.1 s
Using s = ut + 1/2 gt2, we have
2 = u(0.1) × 9.8 (0.1)2
2 = 0.1u 0.049
0.1u = 2 / 0.049
or u = = 19.51 ms-1
This initial velocity at B in motion BC is the final velocity in motion AB. Considering motion AB, we have
u = 0 ; v = 19.51 ms-1; s = ? ; a = 9.8 ms-2
Using v2- u2= 2as, we have
(19.51)2- (0)2= 2 × 9.8 s
or s = 19.4 m
The roof is 19.4 m above the window.
Q6.A ball thrown up is caught by the thrower after 4 s. With what velocity was it thrown up? How high did it go? Where was it after 3 s ? (g = 9.8 m s_2)
Sol. Since the time of going up is the same as that of coming down, therefore time of going up = 4/2 = 2s. Let it start upward with velocity u.
Here u = ?; a = - 9.8 m s-2; t = 2s; v = 0 (at the top); s = h
Using v = u + at
or 0 = u - 9.8 × 2
or u = 19.6 m s-1
Again v2- u2= 2as
0 - (19.6)2= 2 (-9.8) h
h = 19.6 m
After 2s, it starts coming downwards (starting with u = 0). Considering downward motion.
u = 0; a = 9.8 m s-2; t = 3 - 2 = 1s; s = ?
s = ut + 1/2 at2
or s = 0 × 1/2 x 9.8 x (1)2= 4.9 m from top.
Q7. A coconut is hanging on a tree at a height of 15 m from the ground. A boy launches a projectile vertically upwards with a velocity of 20 m s_1. After what time does the projectile pass by the coconut? Explain the two answers in this problem.
Sol. Given:
Displacement, S = +15 m
Initial velocity, u = +20 m/s (upwards)
Acceleration due to gravity, g = −10 m/s²
Time, t =?
Using the equation of motion: S = ut + (1/2)gt²
Substitute the values:
15 = 20t − 5t²
Rearranging the equation:
15 = 20t − 5t²
⇒ 3 = 4t − t²
⇒ t² − 4t + 3 = 0
Solving the quadratic equation:
(t − 1)(t − 3) = 0
∴ Either t − 1 = 0 ⇒ t = 1 s
or t − 3 = 0 ⇒ t = 3 s
Conclusion:
At t = 1s, the projectile passes the coconut while going upwards.
At t = 3s, the projectile passes the coconut while coming downwards.
Q8. What is the force of gravitation between two point masses of 1 kg and 2 kg kept 1 m apart?
Sol.
To calculate the gravitational force (F) between two point masses (m1 and m2) separated by a distance (r), use the formula:
F = (G × m1 × m2) / (r2)
Where:
- F is the gravitational force.
- G is the universal gravitational constant (6.67430 x 10-11 Nm2/kg2).
- m1 and m2 are the masses of the two point masses.
- r is the distance between their centres.
Here, m1 = 1 kg, m2 = 2 kg, and r = 1 m. G is also provided.
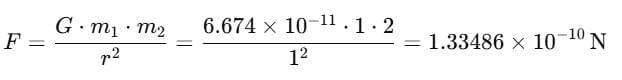
Q9. Calculate the force of gravitation between the Earth and the Sun.Mass of Earth = 6 × 1024 kg, Mass of Sun = 2 × 1030 kg. The average distance between the two is 1.5 × 1011m.
Sol. Given:
Mass of Earth, M1 = 6×1024kg
Mass of Sun, M2 = 2×1030kg
Distance between Earth and Sun, r = 1.5 × 1011m
Gravitational constant, G = 6.674 × 10−11Nm2/kg2
Formula: 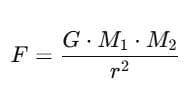
Substitute the values: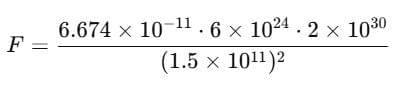
 So, the gravitational force between the Earth and the Sun is approximately 3.56 x 1022 Newtons.
So, the gravitational force between the Earth and the Sun is approximately 3.56 x 1022 Newtons.
Q10. Write down the expression for the acceleration experienced by a particle on the surface of the moon due to the gravitational force of the moon. Find the ratio of this acceleration to that experienced by the same particle on the surface of the Earth. If the acceleration due to gravity on Earth is 9.8 ms-2, what is the acceleration of a particle on the moon's surface? Mass of moon = 7.3 × 1022 kg; Mass of Earth = 6 × 1024 kg. Radius of moon = 1.74 × 106 m, Radius of earth = 6.4 × 106 m.
Sol. The expression for acceleration (am) experienced by a particle on the surface of the Moon due to the gravitational force on the Moon can be calculated using Newton's law of universal gravitation:
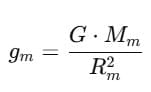
Where:
- am is the acceleration on the surface of the Moon.
- G is the universal gravitational constant (6.67430 x 10-11 Nm2/kg2).
- Mm is the mass of the Moon (7.3 x 1022 kg).
- Rm is the radius of the Moon (1.74 x 106 m).
Now, Substituting the values: 
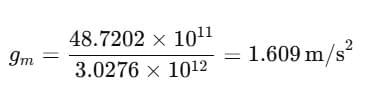
⇒ 
Q11. Find the value of acceleration due to gravity at a height of (a) 6400 km, (b) 12,800 km from the surface of the earth. Radius of earth is 6400 km.
Sol. We know that the acceleration due to gravity at the surface of the Earth is 9.8 m/s².
To find the value of acceleration due to gravity at a height of 6400 km above the surface of the Earth, we can use the formula:
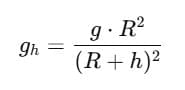
where g is the acceleration due to gravity at the surface of the Earth (9.8 m/s²), R is the radius of the Earth (6400 km), r is the distance from the centre of the Earth (also 6400 km), and h is the height above the surface of the Earth.
(a) When h = 6400 km:
R = 6400km , h = 6400 km
⇒ R+h = 12800 km
Putting in the formula: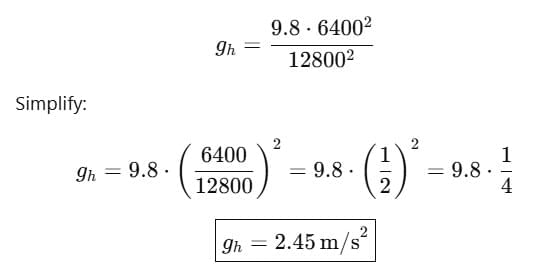
Therefore, the acceleration due to gravity at a height of 6400 km above the surface of the Earth is 2.45 m/s².
(b) h = 12,800km
⇒ R+h = 6400+12800 = 19200 km
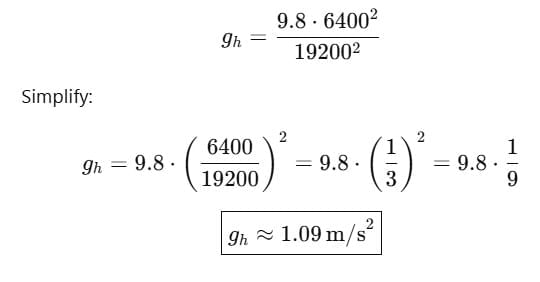
Therefore, the acceleration due to gravity at a height of 12800 km above the surface of the Earth is 1.09 m/s².
Q12. A particle is thrown up vertically with a velocity of 50 m/s. (a) What will be its velocity at the highest point of its journey? (b) How high would the particle rise? (c) What time would it take to reach the highest point?
Sol. (a) At the highest point, the velocity will be zero.
(b) v2- u2= 2as
02-(50)2= 2 (-9.8) × s
5 = 127.5 m
(c) Considering activity A to B
Using v = u at
0 = 50 -9.8 × t
t = 5.1 s
Q13. With reference to the above sample problem, (a) Find the time the particle takes from the highest point back to the initial point (b) Find the velocity with which the particle reaches the initial point.
Sol. The data is given in the adjacent figure. Considering activity B to A
(a) We know that,
v = u + at
50 = 0 + 9.8 (t)
t = 5.1 s
(b) Using v2 - u2 = 2as
v2- 02= 5(9.8)(127.5)
v = 50 m/s
Q14.A ball is dropped from the top of a tower 40 m high. What is its velocity when it has covered 20 m? What would be its velocity when it hits the ground? Take g= 10 m/s2.
Sol. Let point B be at a height of 20 m.
Activity from A to B :
u1= 0, a1= 10 ms_2, s1= 20 m, v1= ?
v12- u12= 2a1s1
v12- 02= 2 (10) (20)
v12=202
v1= 20 m/s
Activity from A to C: C is a point on the ground
u2= 0, a2= 10 ms_2, s2= 40 m, v2= ?
v2 2- u22= 2a2s2
v22- 02= 2 (10) (40)
v22= 800
v2= 28.28 ms_1
Q15.A body is thrown up with a speed of 29.4 ms_1.
(a) What is its speed after (i) t = 1 s, (ii) t = 2 s and (iii) t = 3 s?
(b) What is its height after (i) t = 1 s, (ii) t = 2 s and (iii) t = 3 s?
Sol. (a) (i) u = 29.4 ms_1, a = -9.8 ms_2, t1= 1 s, v1=?
v1= u+ at1
= 29.4 + (-9.8) x 1 = 19.6 ms_1
(ii) u = 29.4 ms, a = -9.8 ms_2, t2 = 2 s, v2 = ?
v2= u + at2
= 29.4 + (-9.8) × 2 = 9.8 ms_1
(iii) u = 29.4 ms_1, a = -9.8 ms_2, t3 = 3 s, v3 = ?
v3= u + at3
= 29.4 + (-9.8) × 3 = 0
(b) Use the formula: 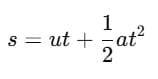
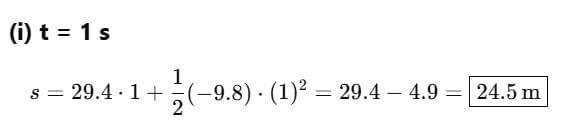
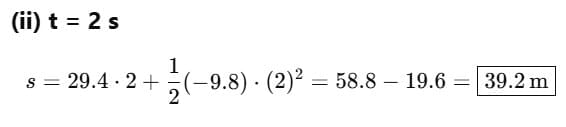
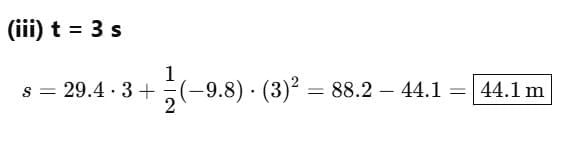
Q16. The weight of a girl is 294 N. Find her mass.
Sol. Weight (W) = Mass (m) × Acceleration due to gravity (g)
Given that the weight of the girl is 294 N and the acceleration due to gravity on Earth is approximately 9.81 m/s², you can rearrange the formula to solve for mass (m):
m = W / g
Substitute the values:
m = 294 N / 9.81 m/s²
Now, calculate the mass:
m ≈ 29.96 kg
So, the mass of the girl is approximately 29.96 kilograms.
Q17. The weight of an object is 294 N on the surface of the Earth. What is its weight at a height of 200 km above the surface of the Earth? Radius of the Earth = 6400 km.
Sol.Weight at a height of 200 km
Wh= mg
Here mg = 294 N, R = 6400 km, h= 200 km
Wh= 294
= 276.45 N
Note:Weight decreases with increase of height from the surface of the earth.
Q18. The gravitational force between two objects is F. How will this force change when
(i) The distance between them is reduced to half?
(ii) The mass of each object is quadrupled?
Sol. (i) According to Newton's law of gravitation, the gravitational force F between two objects a distance r apart is
When the distance between them is reduced to half, i.e., r' = r/2, the force,
Thus, F' = 4F
i.e., force becomes 4 times its previous value.
(ii) Again, according to Newton's law of gravitation, the gravitational force F between two objects of masses m1 and m2 is
F = µ m1m2/ r2
When the mass of each object is quadrupled,
m'1= 4m1 and m'2= 4m2
The force, F ' = µ m'1× m'2/r2
or F' = 16 F
i.e., force becomes 16 times its previous value.
Q19. Calculate the force of gravity acting on your friend of mass 60 kg. Given mass of Earth = 6 x 1024 kg and radius of Earth = 6·4 x 106 m.
Sol.Here, m = 60 kg, M = 6 × 1024kg
R = 6·4 × 106m, F = ?
G = 6·67 × 10-11Nm2/kg2
Thus, 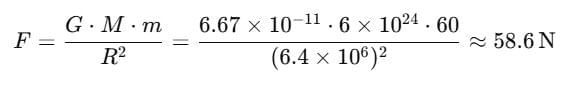
Q20. A block weighing 1·0 kg is in the shape of a cube of length 10 cm. It is kept on a horizontal table. Find the pressure on the portion of the table where the block is kept.
Sol. Given:
- Mass of the block (m) = 1.0 kg
- Acceleration due to gravity (g) ≈ 9.81 m/s²
- Length of one side of the cube (L) = 10 cm = 0.1 m
First, calculate the force (weight) of the block: Weight (F) = m × g
F = 1.0 kg × 9.81 m/s² ≈ 9.81 N
Now, calculate the area (A) of the bottom face of the cube:
A = Length (L) × Width (W)
A = 0.1 m × 0.1 m = 0.01 m²
Now, calculate the pressure (P):
P = F / A
P = 9.81 N / 0.01 m²
P = 981 Pascals (Pa)
Also Check at EduRev
|
84 videos|478 docs|60 tests
|
FAQs on Class 9 Science Chapter 9 Practice Question Answers - Gravitation
| 1. What is the law of universal gravitation? |  |
| 2. How does gravity affect the motion of planets? |  |
| 3. What is the gravitational field strength and how is it calculated? |  |
| 4. What role does gravitational potential energy play in gravitation? |  |
| 5. How does distance affect gravitational force between two objects? |  |