NCERT Solutions Class 11 Maths Chapter 6 - Permutations And Combinations
| Table of contents |

|
| Exercise 6.1 |

|
| Exercise 6.2 |

|
| Exercise 6.3 |

|
| Exercise 6.4 |

|
Exercise 6.1
Q1: How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that
(i) repetition of the digits is allowed? (ii) repetition of the digits is not allowed?
Ans: (i) There will be as many ways as there are ways of filling 3 vacant places 

 in succession by the given five digits. In this case, repetition of digits is allowed. Therefore, the units place can be filled in by any of the given five digits. Similarly, tens and hundreds digits can be filled in by any of the given five digits.
in succession by the given five digits. In this case, repetition of digits is allowed. Therefore, the units place can be filled in by any of the given five digits. Similarly, tens and hundreds digits can be filled in by any of the given five digits.
Thus, by the multiplication principle, the number of ways in which three-digit numbers can be formed from the given digits is 5 × 5 × 5 = 125
(ii) In this case, repetition of digits is not allowed. Here, if units place is filled in first, then it can be filled by any of the given five digits. Therefore, the number of ways of filling the units place of the three-digit number is 5.
Then, the tens place can be filled with any of the remaining four digits and the hundreds place can be filled with any of the remaining three digits.
Thus, by the multiplication principle, the number of ways in which three-digit numbers can be formed without repeating the given digits is 5 × 4 × 3 = 60
Q2: How many 3-digit even numbers can be formed from the digits 1, 2, 3, 4, 5, 6 if the digits can be repeated?
Ans: There will be as many ways as there are ways of filling 3 vacant places 

 in succession by the given six digits. In this case, the units place can be filled by 2 or 4 or 6 only i.e., the units place can be filled in 3 ways. The tens place can be filled by any of the 6 digits in 6 different ways and also the hundreds place can be filled by any of the 6 digits in 6 different ways, as the digits can be repeated.
in succession by the given six digits. In this case, the units place can be filled by 2 or 4 or 6 only i.e., the units place can be filled in 3 ways. The tens place can be filled by any of the 6 digits in 6 different ways and also the hundreds place can be filled by any of the 6 digits in 6 different ways, as the digits can be repeated.
Therefore, by multiplication principle, the required number of three digit even numbers is 3 × 6 × 6 = 108
Q3: How many 4-letter code can be formed using the first 10 letters of the English alphabet, if no letter can be repeated?
Ans: There are as many codes as there are ways of filling 4 vacant places 


 in succession by the first 10 letters of the English alphabet, keeping in mind that the repetition of letters is not allowed.
in succession by the first 10 letters of the English alphabet, keeping in mind that the repetition of letters is not allowed.
The first place can be filled in 10 different ways by any of the first 10 letters of the English alphabet following which, the second place can be filled in by any of the remaining letters in 9 different ways. The third place can be filled in by any of the remaining 8 letters in 8 different ways and the fourth place can be filled in by any of the remaining 7 letters in 7 different ways.
Therefore, by multiplication principle, the required numbers of ways in which 4 vacant places can be filled is 10 × 9 × 8 × 7 = 5040
Hence, 5040 four-letter codes can be formed using the first 10 letters of the English alphabet, if no letter is repeated.
Q4: How many 5–digit telephone numbers can be constructed using the digits 0 to 9 if each number starts with 67 and no digit appears more than once?
Ans: It is given that the 5-digit telephone numbers always start with 67.
Therefore, there will be as many phone numbers as there are ways of filling 3 vacant places  by the digits 0 – 9, keeping in mind that the digits cannot be repeated. The units place can be filled by any of the digits from 0 – 9, except digits 6 and 7. Therefore, the units place can be filled in 8 different ways following which, the tens place can be filled in by any of the remaining 7 digits in 7 different ways, and the hundreds place can be filled in by any of the remaining 6 digits in 6 different ways.
by the digits 0 – 9, keeping in mind that the digits cannot be repeated. The units place can be filled by any of the digits from 0 – 9, except digits 6 and 7. Therefore, the units place can be filled in 8 different ways following which, the tens place can be filled in by any of the remaining 7 digits in 7 different ways, and the hundreds place can be filled in by any of the remaining 6 digits in 6 different ways.
Therefore, by multiplication principle, the required number of ways in which 5-digit telephone numbers can be constructed is 8 × 7 × 6 = 336
Q5: A coin is tossed 3 times and the outcomes are recorded. How many possible outcomes are there?
Ans: When a coin is tossed once, the number of outcomes is 2 (Head and tail) i.e., in each throw, the number of ways of showing a different face is 2. Thus, by multiplication principle, the required number of possible outcomes is 2 × 2 × 2 = 8
Q6: Given 5 flags of different colours, how many different signals can be generated if each signal requires the use of 2 flags, one below the other?
Ans: Each signal requires the use of 2 flags.
There will be as many flags as there are ways of filling in 2 vacant places  in succession by the given 5 flags of different colours.
in succession by the given 5 flags of different colours.
The upper vacant place can be filled in 5 different ways by any one of the 5 flags following which, the lower vacant place can be filled in 4 different ways by any one of the remaining 4 different flags.
Thus, by multiplication principle, the number of different signals that can be generated is 5 × 4 = 20.
Exercise 6.2
Q1: Evaluate
(i) 8!
(ii) 4! – 3!
Ans: (i) 8! = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 = 40320
(ii) 4! = 1 × 2 × 3 × 4 = 24
3! = 1 × 2 × 3 = 6
∴ 4! – 3! = 24 – 6 = 18
Q2: Is 3! 4! = 7!?
Ans: - 3! = 1 × 2 × 3 = 6
4! = 1 × 2 × 3 × 4 = 24
∴ 3! 4! = 6 24 = 30
7! = 1 × 2 × 3 × 4 × 5 × 6 × 7 = 5040
∴ 3! 4! ≠ 7!
Q3: Compute 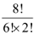
Ans:
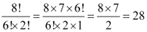
Q4: If 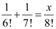 , find x.
, find x.
Ans:
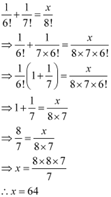
Q5: Evaluate 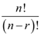 , when
, when
(i) n = 6, r = 2
(ii) n = 9, r = 5
Ans: (i) When n = 6, r = 2, 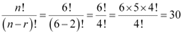
(ii) When n = 9, r = 5, 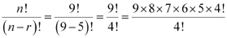
Exercise 6.3
Q1: How many 3-digit numbers can be formed by using the digits 1 to 9 if no digit is repeated?
Ans: 3-digit numbers have to be formed using the digits 1 to 9.
Here, the order of the digits matters.
Therefore, there will be as many 3-digit numbers as there are permutations of 9 different digits taken 3 at a time.
Therefore, required number of 3-digit numbers 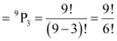
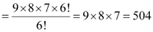
Q2: How many 4-digit numbers are there with no digit repeated?
Ans: The thousands place of the 4-digit number is to be filled with any of the digits from 1 to 9 as the digit 0 cannot be included. Therefore, the number of ways in which thousands place can be filled is 9.
The hundreds, tens, and units place can be filled by any of the digits from 0 to 9. However, the digits cannot be repeated in the 4-digit numbers and thousands place is already occupied with a digit. The hundreds, tens, and units place is to be filled by the remaining 9 digits.
Therefore, there will be as many such 3-digit numbers as there are permutations of 9 different digits taken 3 at a time
Number of such 3-digit numbers 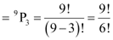
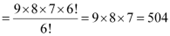
Thus, by multiplication principle, the required number of 4-digit numbers is
9 × 504 = 4536
Q3: How many 3-digit even numbers can be made using the digits 1, 2, 3, 4, 6, 7, if no digit is repeated?
Ans: 3-digit even numbers are to be formed using the given six digits, 1, 2, 3, 4, 6, and 7, without repeating the digits.
Then, units digits can be filled in 3 ways by any of the digits, 2, 4, or 6.
Since the digits cannot be repeated in the 3-digit numbers and units place is already occupied with a digit (which is even), the hundreds and tens place is to be filled by the remaining 5 digits.
Therefore, the number of ways in which hundreds and tens place can be filled with the remaining 5 digits is the permutation of 5 different digits taken 2 at a time.
Number of ways of filling hundreds and tens place 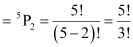
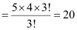
Thus, by multiplication principle, the required number of 3-digit numbers is
3 × 20 = 60
Q4: Find the number of 4-digit numbers that can be formed using the digits 1, 2, 3, 4, 5 if no digit is repeated. How many of these will be even?
Ans: 4-digit numbers are to be formed using the digits, 1, 2, 3, 4, and 5.
There will be as many 4-digit numbers as there are permutations of 5 different digits taken 4 at a time.
Therefore, required number of 4 digit numbers = 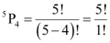
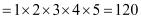
Among the 4-digit numbers formed by using the digits, 1, 2, 3, 4, 5, even numbers end with either 2 or 4.
The number of ways in which units place is filled with digits is 2.
Since the digits are not repeated and the units place is already occupied with a digit (which is even), the remaining places are to be filled by the remaining 4 digits.
Therefore, the number of ways in which the remaining places can be filled is the permutation of 4 different digits taken 3 at a time.
Number of ways of filling the remaining places 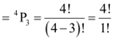
= 4 × 3 × 2 × 1 = 24
Thus, by multiplication principle, the required number of even numbers is
24 × 2 = 48
Q5: From a committee of 8 persons, in how many ways can we choose a chairman and a vice chairman assuming one person cannot hold more than one position?
Ans: From a committee of 8 persons, a chairman and a vice chairman are to be chosen in such a way that one person cannot hold more than one position.
Here, the number of ways of choosing a chairman and a vice chairman is the permutation of 8 different objects taken 2 at a time.
Thus, required number of ways = 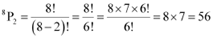
Q6: Find n if 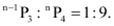
Ans:
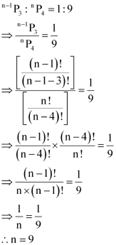
Q7: Find r if (i) 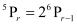
(ii) 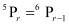 .
.
Ans: (i)
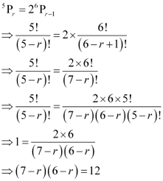
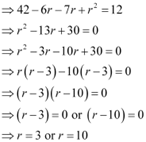
It is known that, 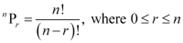
∴ 0 ≤ r ≤ 5
Hence, r ≠ 10
∴ r = 3
(ii)
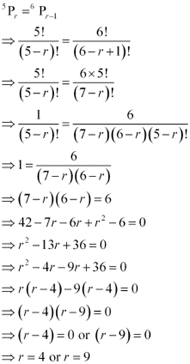
It is known that, 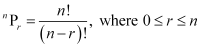
∴ 0 ≤ r ≤ 5
Hence, r ≠ 9
∴ r = 4
Q8: How many words, with or without meaning, can be formed using all the letters of the word EQUATION, using each letter exactly once?
Ans: There are 8 different letters in the word EQUATION.
Therefore, the number of words that can be formed using all the letters of the word EQUATION, using each letter exactly once, is the number of permutations of 8 different objects taken 8 at a time, which is 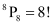 .
.
Thus, required number of words that can be formed = 8! = 40320
Q9: How many words, with or without meaning can be made from the letters of the word MONDAY, assuming that no letter is repeated, if
(i) 4 letters are used at a time,
(ii) all letters are used at a time,
(iii) all letters are used but first letter is a vowel?
Ans: There are 6 different letters in the word MONDAY.
(i) Number of 4-letter words that can be formed from the letters of the word MONDAY, without repetition of letters, is the number of permutations of 6 different objects taken 4 at a time, which is 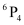 .
.
Thus, required number of words that can be formed using 4 letters at a time is
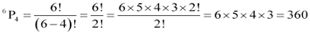
(ii) Number of words that can be formed by using all the letters of the word MONDAY at a time is the number of permutations of 6 different objects taken 6 at a time, which is  .
.
Thus, required number of words that can be formed when all letters are used at a time = 6! = 6×5×4×3×2×1 = 720
(iii) In the given word, there are 2 different vowels, which have to occupy the rightmost place of the words formed. This can be done only in 2 ways.
Since the letters cannot be repeated and the rightmost place is already occupied with a letter (which is a vowel), the remaining five places are to be filled by the remaining 5 letters. This can be done in 5! ways.
Thus, in this case, required number of words that can be formed is
5! × 2 = 120 × 2 = 240
Q10: In how many of the distinct permutations of the letters in MISSISSIPPI do the four I’s not come together?
Ans: In the given word MISSISSIPPI, I appears 4 times, S appears 4 times, P appears 2 times, and M appears just once.
Therefore, number of distinct permutations of the letters in the given word
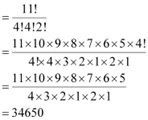
There are 4 Is in the given word. When they occur together, they are treated as a single object  for the time being. This single object together with the remaining 7 objects will account for 8 objects.
for the time being. This single object together with the remaining 7 objects will account for 8 objects.
These 8 objects in which there are 4 Ss and 2 Ps can be arranged in 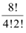 ways i.e., 840 ways.
ways i.e., 840 ways.
Number of arrangements where all Is occur together = 840
Thus, number of distinct permutations of the letters in MISSISSIPPI in which four Is do not come together = 34650 – 840 = 33810
Q11: In how many ways can the letters of the word PERMUTATIONS be arranged if the
(i) words start with P and end with S,
(ii) vowels are all together,
(iii) there are always 4 letters between P and S?
Ans: In the word PERMUTATIONS, there are 2 Ts and all the other letters appear only once.
(i) If P and S are fixed at the extreme ends (P at the left end and S at the right end), then 10 letters are left.
Hence, in this case, required number of arrangements 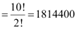
(ii) There are 5 vowels in the given word, each appearing only once.
Since they have to always occur together, they are treated as a single object for the time being. This single object together with the remaining 7 objects will account for 8 objects. These 8 objects in which there are 2 Ts can be arranged in 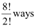 .
.
Corresponding to each of these arrangements, the 5 different vowels can be arranged in 5! ways.
Therefore, by multiplication principle, required number of arrangements in this case 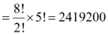
(iii) The letters have to be arranged in such a way that there are always 4 letters between P and S.
Therefore, in a way, the places of P and S are fixed. The remaining 10 letters in which there are 2 Ts can be arranged in 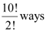 .
.
Also, the letters P and S can be placed such that there are 4 letters between them in 2 × 7 = 14 ways.
Therefore, by multiplication principle, required number of arrangements in this case 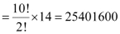
Exercise 6.4
Q1: If 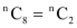 , find
, find 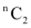 .
.
Ans: It is known that, 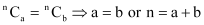
Therefore,
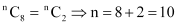
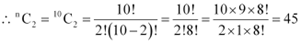
Q2: Determine n if (i) 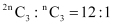 (ii)
(ii)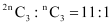
Ans: (i)
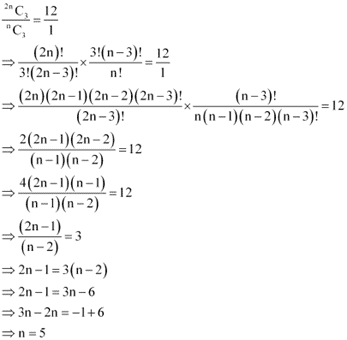
(ii)
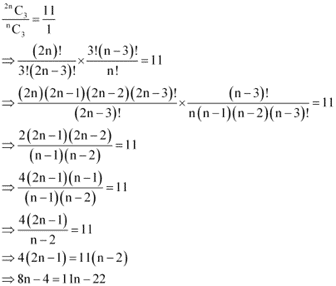
⇒ 11n – 8n = - 4+ 22
⇒ 3n = 18
⇒ n = 6
Q3: How many chords can be drawn through 21 points on a circle?
Ans: For drawing one chord on a circle, only 2 points are required.
To know the number of chords that can be drawn through the given 21 points on a circle, the number of combinations have to be counted.
Therefore, there will be as many chords as there are combinations of 21 points taken 2 at a time.
Thus, required number of chords = 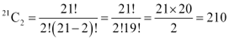
Q4: In how many ways can a team of 3 boys and 3 girls be selected from 5 boys and 4 girls?
Ans: A team of 3 boys and 3 girls is to be selected from 5 boys and 4 girls.
3 boys can be selected from 5 boys in 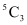 ways.
ways.
3 girls can be selected from 4 girls in 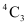 ways.
ways.
Therefore, by multiplication principle, number of ways in which a team of 3 boys and 3 girls can be selected
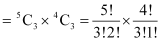
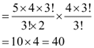
Q5: Find the number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls if each selection consists of 3 balls of each colour.
Ans: There are a total of 6 red balls, 5 white balls, and 5 blue balls.
9 balls have to be selected in such a way that each selection consists of 3 balls of each colour.
Here,
3 balls can be selected from 6 red balls in 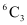 ways.
ways.
3 balls can be selected from 5 white balls in 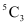 ways.
ways.
3 balls can be selected from 5 blue balls in 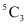 ways.
ways.
Thus, by multiplication principle, required number of ways of selecting 9 balls
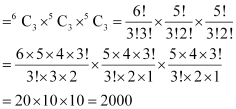
Q6: Determine the number of 5 card combinations out of a deck of 52 cards if there is exactly one ace in each combination.
Ans: In a deck of 52 cards, there are 4 aces. A combination of 5 cards have to be made in which there is exactly one ace.
Then, one ace can be selected in 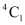 ways and the remaining 4 cards can be selected out of the 48 cards in
ways and the remaining 4 cards can be selected out of the 48 cards in 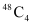 ways.
ways.
Thus, by multiplication principle, required number of 5 card combinations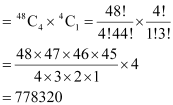
Q7: In how many ways can one select a cricket team of eleven from 17 players in which only 5 players can bowl if each cricket team of 11 must include exactly 4 bowlers?
Ans: Out of 17 players, 5 players are bowlers.
A cricket team of 11 players is to be selected in such a way that there are exactly 4 bowlers.
4 bowlers can be selected in 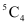 ways and the remaining 7 players can be selected out of the 12 players in
ways and the remaining 7 players can be selected out of the 12 players in 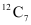 ways.
ways.
Thus, by multiplication principle, required number of ways of selecting cricket team 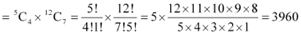
Q8: A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected.
Ans: There are 5 black and 6 red balls in the bag.
2 black balls can be selected out of 5 black balls in 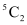 ways and 3 red balls can be selected out of 6 red balls in
ways and 3 red balls can be selected out of 6 red balls in 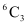 ways.
ways.
Thus, by multiplication principle, required number of ways of selecting 2 black and 3 red balls 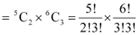
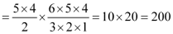
Q9: In how many ways can a student choose a programme of 5 courses if 9 courses are available and 2 specific courses are compulsory for every student?
Ans: There are 9 courses available out of which, 2 specific courses are compulsory for every student.
Therefore, every student has to choose 3 courses out of the remaining 7 courses. This can be chosen in 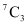 ways.
ways.
Thus, required number of ways of choosing the programme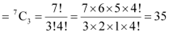
|
172 videos|503 docs|154 tests
|
FAQs on NCERT Solutions Class 11 Maths Chapter 6 - Permutations And Combinations
| 1. What is the difference between permutations and combinations? |  |
| 2. How can permutations and combinations be applied in real-life situations? |  |
| 3. How do you calculate permutations? |  |
| 4. How do you calculate combinations? |  |
| 5. Can permutations and combinations be used in probability calculations? |  |





















