NCERT Solutions Class 11 Maths Chapter 4 - Principle Of Mathematical Induction
NCERT QUESTION - (Principle Of Mathematical Induction)
Question 1: Prove the following by using the principle of mathematical induction or all n ∈ N: 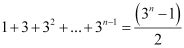
ANSWER: Let the given statement be P(n), i.e.,
P(n): 1 +3+ 32 … 3n–1 = 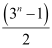
For n = 1, we have
P(1): 1 =  , which is true.
, which is true.
Let P(k) be true for some positive integer k, i.e.,
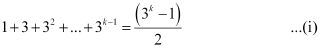
We shall now prove that P(k + 1) is true.
Consider
1+ 3+ 32 … 3k–1 + 3(k 1) – 1
= (1 + 3+ 32 … 3k–1) + 3k
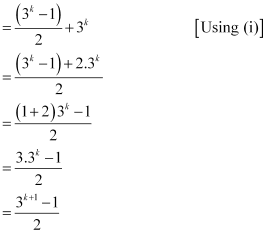
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 2: Prove the following by using the principle of mathematical induction for all n ∈ N: 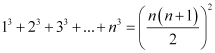
ANSWER: Let the given statement be P(n), i.e.,
P(n): 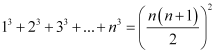
For n = 1, we have
P(1): 13 = 1 = 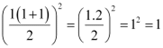 , which is true.
, which is true.
Let P(k) be true for some positive integer k, i.e.,
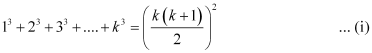
We shall now prove that P(k + 1) is true.
Consider
13 + 23 + 33 … +k3+ (k + 1)3
= (13 + 23 + 33 …. +k3)+ (k + 1)3
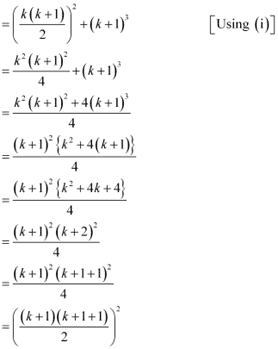
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 3: Prove the following by using the principle of mathematical induction for all n ∈ N: 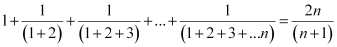
ANSWER: Let the given statement be P(n), i.e.,
P(n): 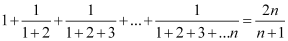
For n = 1, we have
P(1): 1 = 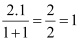 which is true.
which is true.
Let P(k) be true for some positive integer k, i.e.,
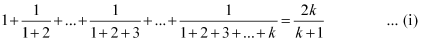
We shall now prove that P(k + 1) is true.
Consider
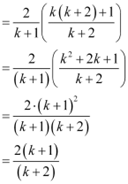
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 4: Prove the following by using the principle of mathematical induction for all n ∈ N: 1.2.3 +2.3.4 … n(n + 1) (n + 2) = 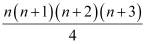 ANSWER: Let the given statement be P(n), i.e.,
ANSWER: Let the given statement be P(n), i.e.,
P(n): 1.2.3+ 2.3.4 … n(n + 1) (n+ 2) = 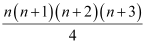
For n = 1, we have
P(1): 1.2.3 = 6 = 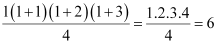 , which is true.
, which is true.
Let P(k) be true for some positive integer k, i.e.,
1.2.3 + 2.3.4 … k(k + 1) (k + 2) 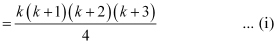
We shall now prove that P(k + 1) is true.
Consider
1.2.3+ 2.3.4 … +k(k + 1) (k + 2)+ (k + 1) (+k 2) (k + 3)
= {1.2.3 + 2.3.4 … k(k + 1) (k + 2)} + (k + 1) (k + 2) (k + 3)
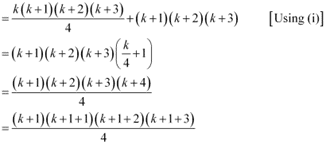
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 5: Prove the following by using the principle of mathematical induction for all n ∈ N: 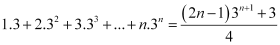
ANSWER: Let the given statement be P(n), i.e.,
P(n) : 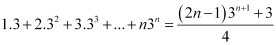
For n = 1, we have
P(1): 1.3 = 3 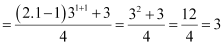 , which is true.
, which is true.
Let P(k) be true for some positive integer k, i.e.,
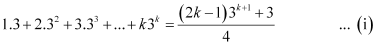
We shall now prove that P(k + 1) is true.
Consider
1.3+ 2.32 + 3.33 … +k3k +(k +1) 3k 1
= (1.3+ 2.32 + 3.33 … +k.3k)+ (k + 1) 3k+ 1
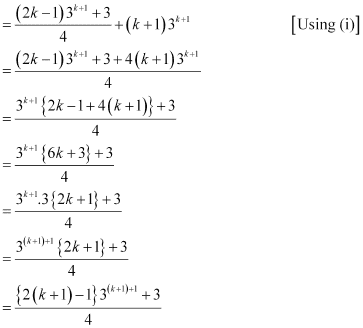
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 6:Prove the following by using the principle of mathematical induction for all n ∈ N: 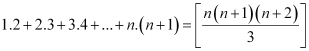
ANSWER: Let the given statement be P(n), i.e.,
P(n): 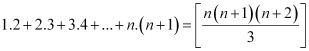
For n = 1, we have
P(1): 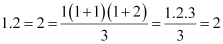 , which is true.
, which is true.
Let P(k) be true for some positive integer k, i.e.,
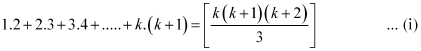
We shall now prove that P(k + 1) is true.
Consider
1.2+ 2.3 +3.4 … +k.(k+ 1) +(k + 1).(k + 2)
= [1.2+ 2.3 +3.4 … +k.(k +1)] +(k + 1).(k + 2)
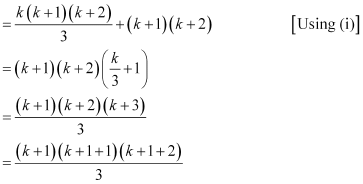
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 7: Prove the following by using the principle of mathematical induction for all n ∈ N: 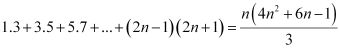
ANSWER: Let the given statement be P(n), i.e.,
P(n): 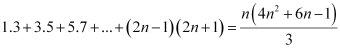
For n = 1, we have
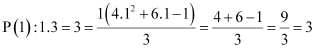 , which is true.
, which is true.
Let P(k) be true for some positive integer k, i.e.,
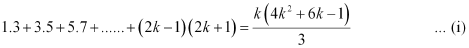
We shall now prove that P(k + 1) is true.
Consider
(1.3+ 3.5+5.7 … (2k – 1) (2k + 1) +{2(k + 1) – 1}{2(k+ 1) +1}
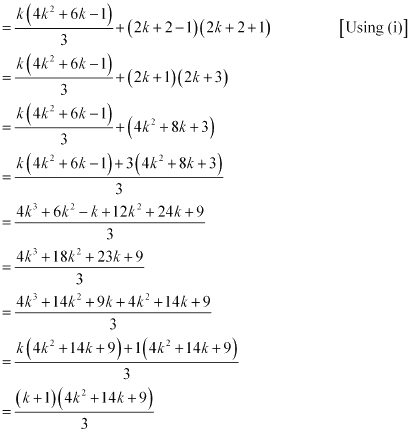
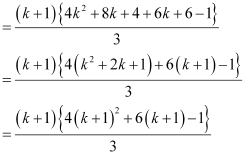
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 8: Prove the following by using the principle of mathematical induction for all n ∈ N: 1.2+ 2.22 + 3.22 … +n.2n = (n – 1) 2n+ 1 + 2
ANSWER: Let the given statement be P(n), i.e.,
P(n): 1.2+ 2.22 + 3.22+ … +n.2n = (n – 1) 2n+ 1 + 2
For n = 1, we have
P(1): 1.2 = 2 = (1 – 1) 21+ 1+ 2 = 0+ 2 = 2, which is true.
Let P(k) be true for some positive integer k, i.e.,
1.2 +2.22 +3.22 + … + k.2k = (k – 1) 2k+ 1 + 2 … (i)
We shall now prove that P(k +1) is true.
Consider
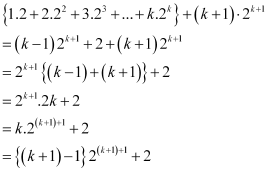
Thus, P(k +1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 9: Prove the following by using the principle of mathematical induction for all n ∈ N: 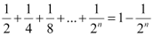
ANSWER: Let the given statement be P(n), i.e.,
P(n): 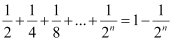
For n = 1, we have
P(1): 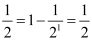 , which is true.
, which is true.
Let P(k) be true for some positive integer k, i.e.,
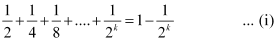
We shall now prove that P(k +1) is true.
Consider
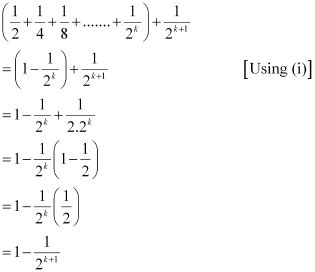
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 10: Prove the following by using the principle of mathematical induction for all n ∈ N: 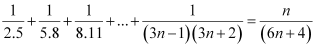
ANSWER: Let the given statement be P(n), i.e.,
P(n): 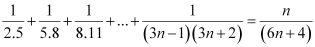
For n = 1, we have
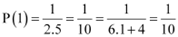 , which is true.
, which is true.
Let P(k) be true for some positive integer k, i.e.,
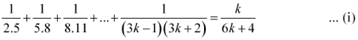
We shall now prove that P(k + 1) is true.
Consider
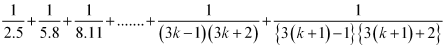
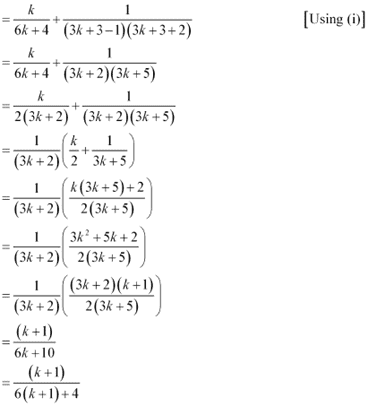
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 11: Prove the following by using the principle of mathematical induction for all n ∈ N: 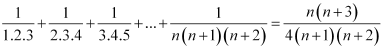
ANSWER: Let the given statement be P(n), i.e.,
P(n): 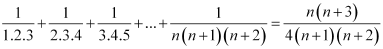
For n = 1, we have
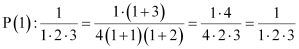 , which is true.
, which is true.
Let P(k) be true for some positive integer k, i.e.,

We shall now prove that P(k + 1) is true.
Consider
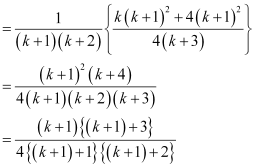
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 12: Prove the following by using the principle of mathematical induction for all n ∈ N: 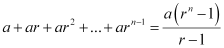
ANSWER: Let the given statement be P(n), i.e.,
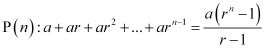
For n = 1, we have
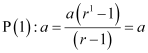 , which is true.
, which is true.
Let P(k) be true for some positive integer k, i.e.,
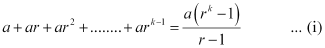
We shall now prove that P(k + 1) is true.
Consider
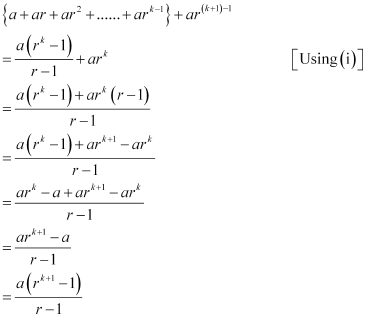
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 13: Prove the following by using the principle of mathematical induction for all n ∈ N: 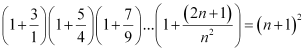
ANSWER: Let the given statement be P(n), i.e.,
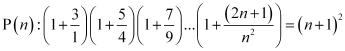
For n = 1, we have
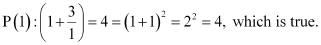
Let P(k) be true for some positive integer k, i.e.,
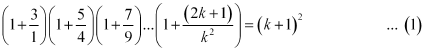
We shall now prove that P(k + 1) is true.
Consider
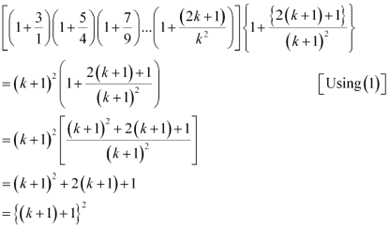
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 14: Prove the following by using the principle of mathematical induction for all n ∈ N:
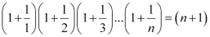
ANSWER: Let the given statement be P(n), i.e.,
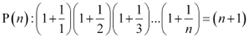
For n = 1, we have
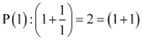 , which is true.
, which is true.
Let P(k) be true for some positive integer k, i.e.,
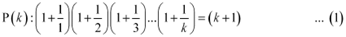
We shall now prove that P(k + 1) is true.
Consider
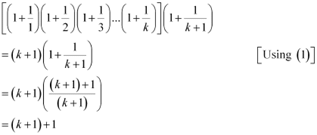
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 15: Prove the following by using the principle of mathematical induction for all n ∈ N: 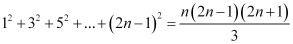
ANSWER: Let the given statement be P(n), i.e.,
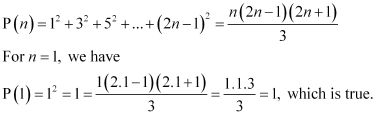
Let P(k) be true for some positive integer k, i.e.,
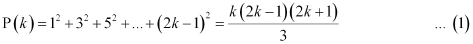
We shall now prove that P(k + 1) is true.
Consider
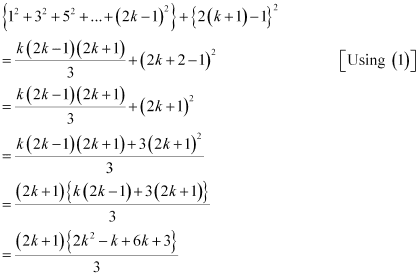
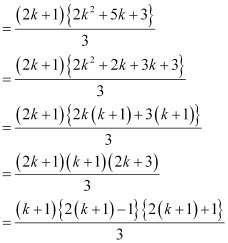
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 16:Prove the following by using the principle of mathematical induction for all n ∈ N: 
ANSWER: Let the given statement be P(n), i.e.,
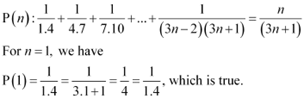
Let P(k) be true for some positive integer k, i.e.,
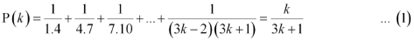
We shall now prove that P(k + 1) is true.
Consider
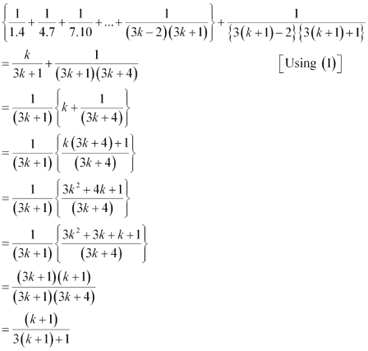
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 17: Prove the following by using the principle of mathematical induction for all n ∈ N: 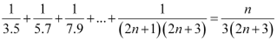
ANSWER: Let the given statement be P(n), i.e.,
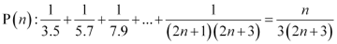
For n = 1, we have
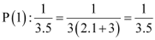 , which is true.
, which is true.
Let P(k) be true for some positive integer k, i.e.,
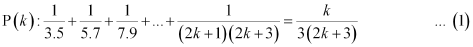
We shall now prove that P(k + 1) is true.
Consider
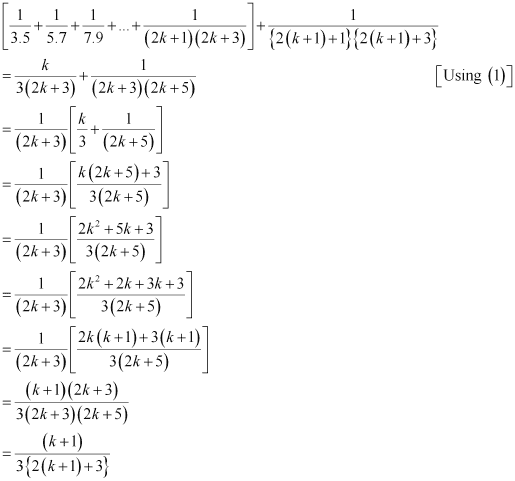
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 18: Prove the following by using the principle of mathematical induction for all n ∈ N: 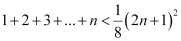
ANSWER: Let the given statement be P(n), i.e.,
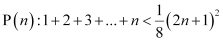
It can be noted that P(n) is true for n = 1 since 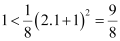 .
.
Let P(k) be true for some positive integer k, i.e.,
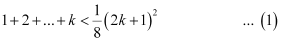
We shall now prove that P(k + 1) is true whenever P(k) is true.
Consider
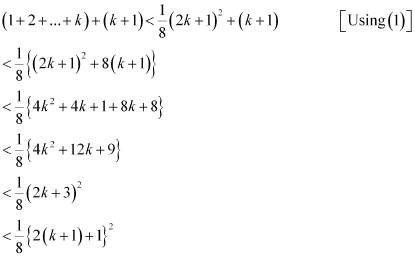
Hence, 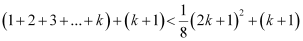
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 19: Prove the following by using the principle of mathematical induction for all n ∈ N: n (n+ 1) (n + 5) is a multiple of 3.
ANSWER: Let the given statement be P(n), i.e.,
P(n): n (n + 1) (n + 5), which is a multiple of 3.
It can be noted that P(n) is true for n = 1 since 1 (1+ 1) (1 +5) = 12, which is a multiple of 3.
Let P(k) be true for some positive integer k, i.e.,
k (k + 1) (k + 5) is a multiple of 3.
∴k (k + 1) (k +5) = 3m, where m ∈ N … (1)
We shall now prove that P(k + 1) is true whenever P(k) is true.
Consider
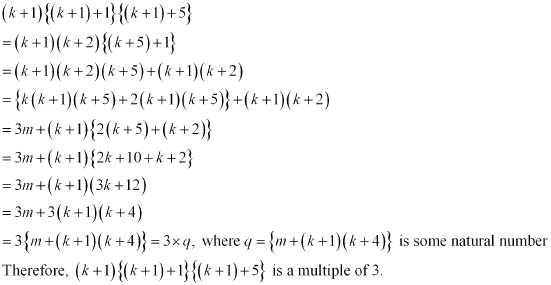
Thus, P(k +1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 20: Prove the following by using the principle of mathematical induction for all n ∈ N: 102n – 1 +1 is divisible by 11.
ANSWER: Let the given statement be P(n), i.e.,
P(n): 102n – 1 +1 is divisible by 11.
It can be observed that P(n) is true for n = 1 since P(1) = 102.1 – 1 +1 = 11, which is divisible by 11.
Let P(k) be true for some positive integer k, i.e.,
102k – 1 + 1 is divisible by 11.
∴102k – 1 +1 = 11m, where m ∈ N … (1)
We shall now prove that P(k + 1) is true whenever P(k) is true.
Consider

Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 21: Prove the following by using the principle of mathematical induction for all n ∈ N: x2n – y2n is divisible by x + y.
ANSWER: Let the given statement be P(n), i.e.,
P(n): x2n – y2n is divisible by x + y.
It can be observed that P(n) is true for n = 1.
This is so because x2 × 1 – y2 × 1 = x2 – y2 = (x + y) (x – y) is divisible by (x + y).
Let P(k) be true for some positive integer k, i.e.,
x2k – y2k is divisible by x + y.
∴x2k – y2k = m (x + y), where m ∈ N … (1)
We shall now prove that P(k + 1) is true whenever P(k) is true.
Consider
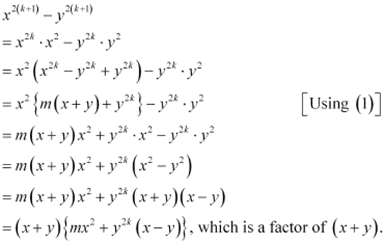
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 22: Prove the following by using the principle of mathematical induction for all n ∈ N: 32n+ 2 – 8n – 9 is divisible by 8.
ANSWER: Let the given statement be P(n), i.e.,
P(n): 32n+ 2 – 8n – 9 is divisible by 8.
It can be observed that P(n) is true for n = 1 since 32 × 1 +2 – 8 × 1 – 9 = 64, which is divisible by 8.
Let P(k) be true for some positive integer k, i.e.,
32k+ 2 – 8k – 9 is divisible by 8.
∴32k + 2 – 8k – 9 = 8m; where m ∈ N … (1)
We shall now prove that P(k + 1) is true whenever P(k) is true.
Consider
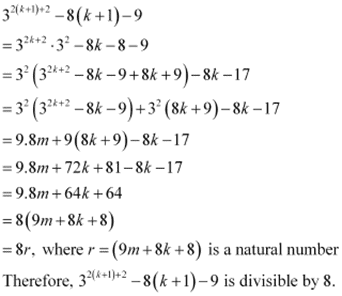
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 23: Prove the following by using the principle of mathematical induction for all n ∈ N: 41n – 14n is a multiple of 27.
ANSWER: Let the given statement be P(n), i.e.,
P(n):41n – 14n is a multiple of 27.
It can be observed that P(n) is true for n = 1 since 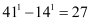 , which is a multiple of 27.
, which is a multiple of 27.
Let P(k) be true for some positive integer k, i.e.,
41k – 14k is a multiple of 27
∴41k – 14k = 27m, where m ∈ N … (1)
We shall now prove that P(k + 1) is true whenever P(k) is true.
Consider
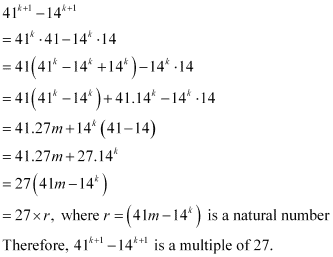
Thus, P(k +1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 24: Prove the following by using the principle of mathematical induction for all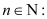 (2n +7) < (n + 3)2
(2n +7) < (n + 3)2
ANSWER: Let the given statement be P(n), i.e.,
P(n): (2n + 7) < (n + 3)2
It can be observed that P(n) is true for n = 1 since 2.1+ 7 = 9 < (1+ 3)2 = 16, which is true.
Let P(k) be true for some positive integer k, i.e.,
(2k + 7) < (k + 3)2 … (1)
We shall now prove that P(k + 1) is true whenever P(k) is true.
Consider
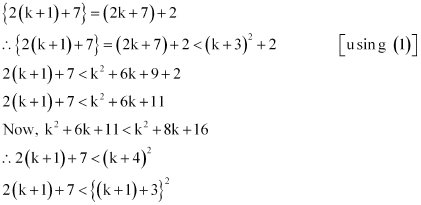
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
|
73 videos|264 docs|91 tests
|
FAQs on NCERT Solutions Class 11 Maths Chapter 4 - Principle Of Mathematical Induction
| 1. How do you prove a statement using the principle of mathematical induction? |  |
| 2. What is the base case in a proof by mathematical induction? |  |
| 3. Is mathematical induction the only way to prove mathematical statements? |  |
| 4. Can mathematical induction be used to prove inequalities? |  |
| 5. How can mathematical induction be applied to solve problems in combinatorics or number theory? |  |






















