NCERT Solutions Class 11 Maths Chapter 3 - Trigonometric Functions
Q1: Find the radian measures corresponding to the following degree measures:
(i) 25°
(ii) – 47° 30'
(iii) 240°
(iv) 520°
Ans:
(i) 25°
We know that 180° = π radian

(ii) –47° 30'
= 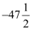 degree [1° = 60']
degree [1° = 60']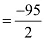 degree
degree
Since 180° = π radian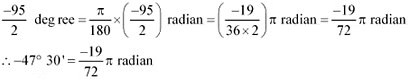
(iii) 240°
We know that 180° = π radian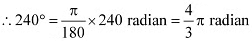
(iv) 520°
We know that 180° = π radian
Q2: Find the degree measures corresponding to the following radian measures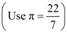 .
.
(i) 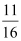
(ii) – 4
(iii) 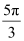
(iv) 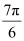
Ans: (i) 11/16
We know that π radian = 180°

(ii) – 4
We know that π radian = 180°
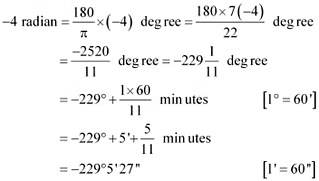
(iii) 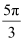
We know that π radian = 180°
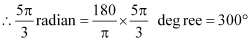
(iv) 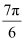
We know that π radian = 180°
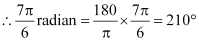
Q3: A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?
Ans: Number of revolutions made by the wheel in 1 minute = 360
∴ Number of revolutions made by the wheel in 1 second = 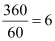
In one complete revolution, the wheel turns an angle of 2π radian.
Hence, in 6 complete revolutions, it will turn an angle of 6 × 2π radian, i.e., 12 π radian
Thus, in one second, the wheel turns an angle of 12π radian.
Q4: Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm 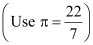 Ans: We know that in a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre, then
Ans: We know that in a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre, then
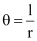
Therefore, for r = 100 cm, l = 22 cm, we have
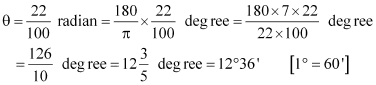
Thus, the required angle is 12°36′.
Q5: In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.
Ans: Diameter of the circle = 40 cm 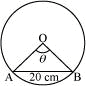
∴Radius (r) of the circle = 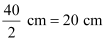
Let AB be a chord (length = 20 cm) of the circle.
In ΔOAB, OA = OB = Radius of circle = 20 cm
Also, AB = 20 cm
Thus, ΔOAB is an equilateral triangle.
∴ θ = 60° = 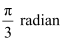
We know that in a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre, then 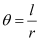 .
.
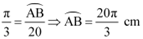
Thus, the length of the minor arc of the chord is 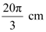 .
.
Q6: If in two circles, arcs of the same length subtend angles 60° and 75° at the centre, find the ratio of their radii.
Ans: Let the radii of the two circles be 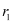 and
and 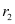 . Let an arc of length l subtend an angle of 60° at the centre of the circle of radius r1, while let an arc of length l subtend an angle of 75° at the centre of the circle of radius r2.
. Let an arc of length l subtend an angle of 60° at the centre of the circle of radius r1, while let an arc of length l subtend an angle of 75° at the centre of the circle of radius r2.
Now, 60° = 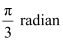 and 75° =
and 75° = 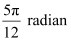
We know that in a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre, then 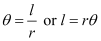 .
.
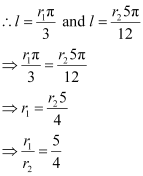
Thus, the ratio of the radii is 5:4.
Q7: Find the angle in radian though which a pendulum swings if its length is 75 cm and the tip describes an arc of length
(i) 10 cm
(ii) 15 cm
(iii) 21 cm
Ans: We know that in a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre, then  .
.
It is given that r = 75 cm
(i) Here, l = 10 cm
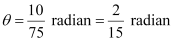
(ii) Here, l = 15 cm
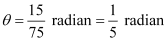
(iii) Here, l = 21 cm
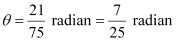
|
176 videos|582 docs|160 tests
|
FAQs on NCERT Solutions Class 11 Maths Chapter 3 - Trigonometric Functions
| 1. What are the basic trigonometric functions? |  |
| 2. What is the unit circle and its relation to trigonometric functions? |  |
| 3. How can trigonometric functions be used to solve real-life problems? |  |
| 4. What is the reciprocal relationship between trigonometric functions? |  |
| 5. How can trigonometric functions be used in calculus and physics? |  |

















