Optical Isomerism | Chemistry Class 11 - NEET PDF Download
Optical isomerism is a case where the isomers display identical characteristics in terms of molecular weight as well as chemical and physical properties. However, they differ in their effect on the rotation of polarized light.
- Optical isomerism occurs mainly in substances that have the same molecular and structural formula, but they cannot be superimposed on each other.
- In simple words, we can say that they are mirror images of each other. Alternatively, it can also be found in substances that have an asymmetric carbon atom.
 Depiction of Mirror Images of Alanine.
Depiction of Mirror Images of Alanine.
What is Plane Polarized Light?
If by filtering the beam with specialized materials, the electric field vectors are limited to a single plane, then the light is referred to as plane or linearly polarised with respect to the propagation direction. All waves vibrating in a single plane are referred to as plane-parallel or plane-polarized.
 Plane Polarized Light
Plane Polarized Light
Optical Isomerism & Plane Polarized Light
- Optical isomerism is shown by stereoisomers which rotate the plane of polarized light.
- If the plane of polarized light passing through the enantiomer solution rotates in the clockwise direction then the enantiomer is said to exist as (+) form and if the plane of polarized light rotates in an anti-clockwise direction then the enantiomer is said to exist in (-).

- If the rotation of light is anti-clockwise then laevo rotatory (l-form)
- If the rotation of light is clockwise then dextro rotatory substance(d-form)
- If there is no rotation of light then the substance is called optically inactive.
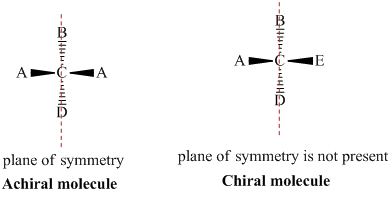
Chiral and Achiral Molecules
Chiral and achiral molecules are used to describe the symmetry characteristics of molecules. There are two main criteria to determine if a molecule is chiral or achiral:
- On the Basis of Atoms Attached
- On the Basis of Plane of Symmetry
- A chiral molecule is a molecule that is not superimposable on its mirror image. In other words, it does not possess an internal plane of symmetry.
- Achiral molecules are those that possess a plane of symmetry and are superimposable on their mirror image.
 Superimposable and Nonsuperimposable Nature of Chiral and Achiral Objects
Superimposable and Nonsuperimposable Nature of Chiral and Achiral Objects
Here are the details with examples of Chiral and Achiral Objects
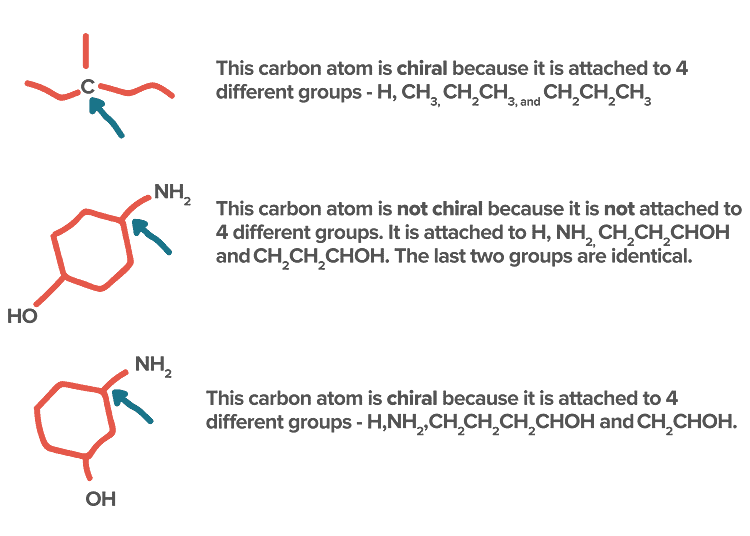
1. On the Basis of Atoms Attached:
- If in a molecule, all the four valencies of carbon are satisfied by four different atoms or four different group atoms then carbon is known as chiral carbon and the molecule is called Chiral.
 Achiral and Chiral Compounds
Achiral and Chiral Compounds
- If in a molecule, all the four valencies of carbon are not satisfied by four different atoms or four different group atom then carbon is known as achiral carbon and molecule is called Achiral.
 Identification of Chiral and Achiral CarbonsSome other Examples:
Identification of Chiral and Achiral CarbonsSome other Examples:

 (2 Chiral carbon)
(2 Chiral carbon)
-
 (2 Chiral carbon)
(2 Chiral carbon)
-
 (no chiral carbon)
(no chiral carbon)
2. On the Basis of Plane of Symmetry:
- If the molecule having chiral center (four different groups are attached) and not having the plane of symmetry or axis of symmetry then it is called Chiral molecule.
- If the molecule is having the plane of symmetry or axis of symmetry is then it is called achiral molecule. Achiral molecule not have chiral center.

Examples:

(Achiral due to plane of symmetry)
What are Enantiomers and Diastereomers?
Enantiomers and diastereomers are terms used to describe different types of stereoisomers, which are molecules that have the same molecular formula and connectivity but differ in their spatial arrangement.
 Flow Chart Explaining Enantiomers and Diastereomers
Flow Chart Explaining Enantiomers and Diastereomers
Enantiomers
Enantiomers are a pair of molecules that exist in two forms that can not be superimposed on each other but are mirror images of each other.
 Enantiomers: Non-Superimposable Mirror images
Enantiomers: Non-Superimposable Mirror images
- Enantiomers are a pair of molecules that have the same chemical formula and connectivity but differ in their three-dimensional arrangement. They cannot be superimposed on each other, similar to how our hands are mirror images but cannot be perfectly overlapped.
- Enantiomers share similar physical and chemical properties, but they exhibit different optical behavior. When plane-polarized light is passed through enantiomers, they demonstrate different optical properties, such as the direction and degree of rotation of the light.
- If we imagine placing a mirror between the two enantiomers and looking at one of them, we would see the other enantiomer reflected in the mirror. This is because the original enantiomer and its mirror image have distinct spatial arrangements and are considered enantiomers.
- It is important to note that if an object and its mirror image can be superimposed, they are not enantiomers. Enantiomers are specifically defined as non-superimposable mirror images.
However, if an object and its mirror image cannot be superimposed, they are optically active and referred to as enantiomers.
To determine if an object and its mirror image are superimposable, we can perform a test. Either the object or its mirror image is rotated by 180 degrees along with the mirror. After this rotation, we examine if the mirror image can be overlapped perfectly with the original object. Let us consider two examples:
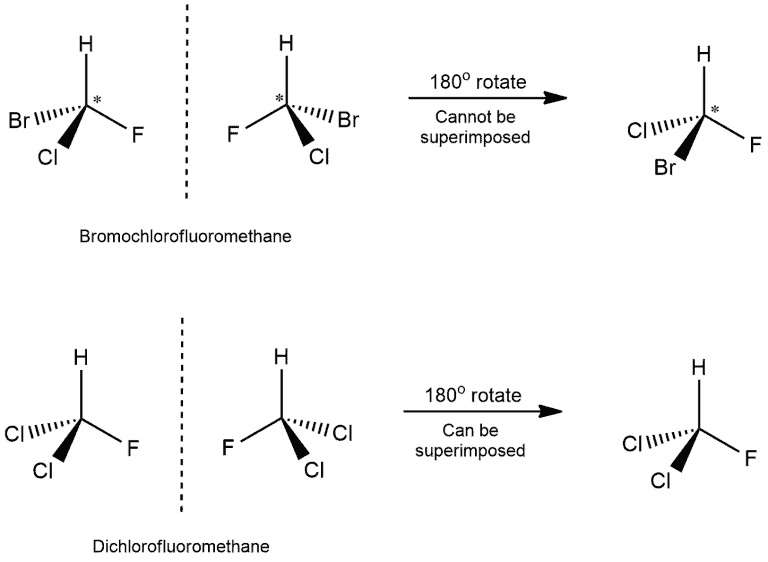
- In the first example, we can see that four different atoms are attached to the carbon atom. Those are bromine, chlorine, fluorine, and hydrogen. The chiral center is marked by a star (*), which is the usual way of marking it.
- When we would put the mirror next to the molecule on the left, we would get the molecule on the right. Then, if we would rotate this molecule by 180 degrees, we wouldn’t get the same molecule as on the left. Hydrogen and fluorine will be in the same position but chlorine and bromine on the opposite. And because of that, we get non-superimposable structures.
- While in the other example, we have two chlorine atoms attached to the carbon. When we rotate the mirror image, we get the same molecule as on the left! This means that this molecule has superimposable structure.
Determining Enantiomers through R,S Assignments
- For two molecules with the same connectivity: The enantiomer of a molecule will always have an opposite R/S configuration. So to get the enantiomer of (2R, 3R, 4R)-2,3,4,5-tetrahydroxypentanal all we need to do is flip all the stereocenters: (2S, 3S, 4S)
 R-S Configuration of Enantiomers
R-S Configuration of Enantiomers
- The R and S designations, derived from the Cahn-Ingold-Prelog priority rules, are commonly used to differentiate enantiomers and establish their spatial configurations. We have covered about Cahn-Ingold-Prelog Rules in detail later in this document.
Some Solved Examples on Determining Enantiomers
Q.1. Which of the following pairs of compounds is a pair of enantiomers ?
A.
B.
C. 
D.

Solution: The correct option is B
- In option (d), one of the isomer has a plane of symmetry so it won't show chirality and hence, it cannot be its enantiomeric pair.
- Cyclohexane molecules exist in chair form and they does not have a plane of symmetry in the ring. Both the isomers in option (c) are not mirror images. Hence, they are not enantiomers.
- In option (a), both the structures are identical. They have same configuration about the chiral centres.

- In (b), both are mirror image along the plane of paper and are not superimposable on each other. So, they are enantiomers.
Hence, (b) is correct.
Q.2. Which of the following is capable of existing as a pair of enantiomers?
A. 3-Methylpentane
B. 3-Methylhexane
C. 2-Methylpentane
D. 2-Methylpropane
Solution: 3- Methylhexane is optically active because of molecular unsymmetry and chiral carbon. Hence it is capable of existing as a pair of enantiomers. 3-Methylhexane
3-Methylhexane
Diastereomers
A diastereomer is a stereoisomer with two or more stereocenters and the isomers are not mirror images of each other.
- If a molecule has more than one stereocenter and every single stereocenter isn’t in the opposite direction then they are not enantiomers, but diastereomers.
- In the following example, we have three stereocenters. On the first and third configuration is different (which would resemble the enantiomers) but on the second stereocenter is the same configuration. This means that they aren’t enantiomers but diastereomers.

Example: Enantiomers and Diastereomers through Mirror Images:
 Identifying Enantiomers and Diastereomers through Mirror Images
Identifying Enantiomers and Diastereomers through Mirror Images
Determining Diastereomers through R,S Assignments
You can also tell if molecules are diastereomers by looking at their R,S designations.
For two molecules with the same connectivity:
- The enantiomer of a molecule will always have an opposite R/S configuration.
- Diastereomers arise when at least two molecules share at least one (but not all) chiral center(s) with identical (R/S) configuration. So to find the diastereomers of (2R,3R,4R)-2,3,4,5-tetrahydroxypentanal , all we need to do is keep at least one stereocenter the same, and flip any or all of the rest.
 Determining Enantiomers and Diastereomers through R-S Configuration
Determining Enantiomers and Diastereomers through R-S Configuration
The following rule can be applied to all molecules with two stereocenters: R-S configuration in Enantiomers and Diasteromers
R-S configuration in Enantiomers and Diasteromers

Types of Representations of Molecules in 3d
Different types of representations can be used to depict the three-dimensional (3-D) structure of organic molecules on paper. There are mainly four types of representations of organic molecules in three dimensions:
- Wedge Dash
- Fischer Projection
- Sawhorse
- Newman Projection
Wedge Dash Representation
A Wedge Dash, the most popular three-dimensional depiction of a molecule on a two-dimensional surface is in projection (paper). This type of representation is typically used for molecules with chiral centres. This type of representation employs three different types of lines.

- Solid wedges or thick lines signify bond projections towards the observer or above the paper's surface. A continuous or regular line denotes a bond in the plane of the paper.
- A bond projection away from the observer is indicated by a dashed or broken line.
Fischer Projection
Fischer projections are best used to represent the straight-chain structures of monosaccharides and some amino acids. They represent structural forms that allow one to convey valuable stereochemical information by drawing 3D molecules as flat structures.
How to Draw Fischer Projection?
In a Fischer projection, the longest chain is drawn vertically. The horizontal lines indicate the bonds with hydrogen, hydroxyl, and amino groups. The four bonds to a chiral carbon make a cross, with the carbon atom at the intersection of the horizontal and vertical lines. The following steps can be employed for an aldohexose.
Step 1: Arrange the molecule so that the chiral carbons and the longest continuous chain are in a vertical line. The aldehyde group representing carbon 1 goes at the top
Step 2: Draw horizontal lines to make crosses at C-2, C-3, C-4, and C-5.
Step 3: Put the OH groups on the exact side of the cross.
Step 4: Remove C-2, C-3, C-4, and C-5, and the Fischer projection is obtained.
Fischer Projection Rules
The following rules should be kept in mind while working with Fischer projection.
- Fischer projection may be rotated by 180 degrees without changing its meaning.
- Fischer projection may not be rotated by 90 degrees. Such a rotation typically changes the configuration to the enantiomer.
- To find the enantiomer of a molecule drawn as Fischer projection, exchange the right and left horizontal bonds.
Converting Wedge-Dash Structure to Fischer Projection
The stereochemical formula for (R)-lactic acid can be drawn using the wedge-dashed structure and Fischer projection method. The conversion from wedge-shaped or bond-line structure to Fischer projection is done stepwise.Examples:
Q.1. Write the Fisher projection of CH3CH(OH)COOH
Sol.

- Maximum carbon must be in a vertical line.
- Place higher priority carbon-containing functional group on top of the vertical line.
Q.2 Write Fisher projection of

Sol.
(i) Place a higher-priority carbon-containing functional group on top of the vertical line.
(ii) Arrange another group according to its clockwise or anti-clockwise position w.r.t. group on the top.

Q.3. Convert the following wedge-dash figure in the fischer projection. Sol.
Sol.
Q.4. Out of the two cross lines in the representation of Fischer projection, what does the horizontal line represent?
Ans: The Fischer Projection consists of both horizontal and vertical lines, where the horizontal lines represent the atoms that are pointed out of the plane while the vertical line represents atoms that are pointed away from the plane. The point of intersection between the horizontal and vertical lines represents the central carbon.

Q.5. Draw the fisher projection of:

Sol.
 *
* 
If fourth valency is not given then we assume it to be hydrogen.
Assigning R-S Configuration in Wedge Dash
 R → Rectus → Right → Clock wise.
R → Rectus → Right → Clock wise.
 S → Sinister → Left → Anti-clockwise.
S → Sinister → Left → Anti-clockwise.
The Cahn Ingold Prelog (CIP) System For Naming Chiral Centers
- Priority order: The Cahn Ingold Prelog (CIP) system is used to name chiral centers based on their priority. The groups around the chiral center are ranked from highest to lowest atomic number, with #1 being the highest and #4 being the lowest.
example:





To determine the configuration (R/S) of the chiral center:
- Position the chiral center so that the #4 priority substituent is pointing away from you, indicated by a "dashed" bond.
- Trace the path from priorities #1 to #2 to #3, ignoring #4.
- If the path traced is clockwise, the chiral center is assigned (R). If it is counterclockwise, the chiral center is assigned (S).
(i) Determining R/S When The #4 Substituent Is In Back (i.e. on a “Dash”)
When the #4 substituent is in the back (on a "dash"), follow the regular rules mentioned above. Here is the example:
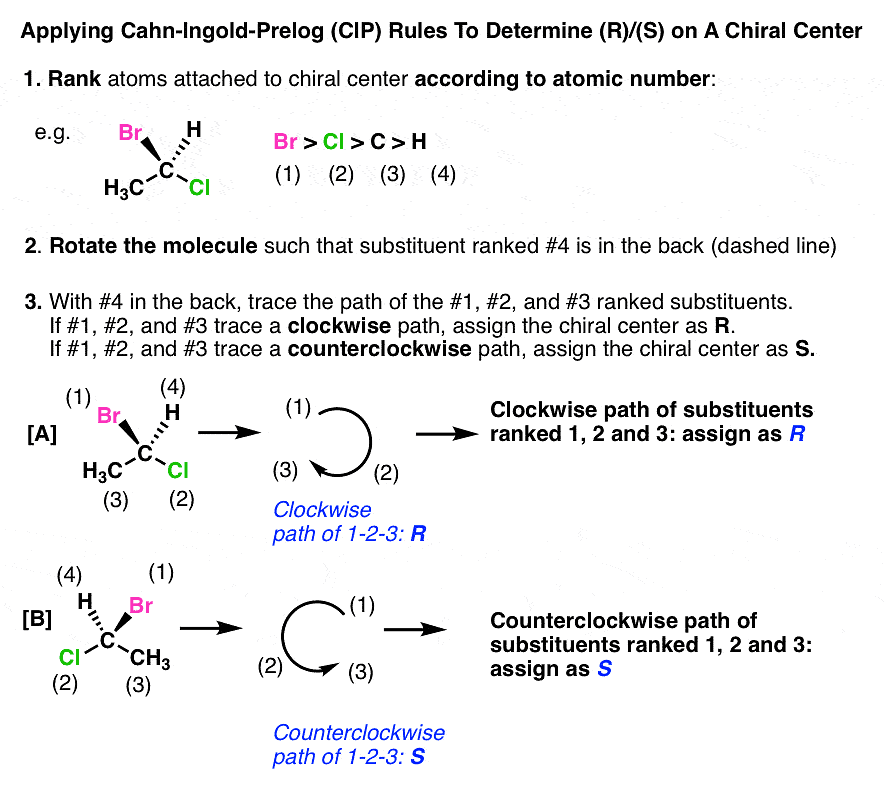
Note: Designations (R) and (S) bear no relationship to whether a molecule rotates plane-polarized light clockwise (+) or counterclockwise (-).
(ii)
Determining R/S When The #4 Substituent Is In Front (i.e. on a “Wedge”)
Let’s first consider the molecule below. The name of this molecule is (R)-1-fluoroethanol. It is listed below with priorities assigned based on atomic number. In this case F>O>C>H. So F is #1 and H is #4. The tricky part here is that the #4 priority is pointing out of the page (on a “wedge”).
You can “simply” rotate the molecule in your head so that the #4 priority is on a dash. Then you can assign R or S in the traditional way. This “simple” advice is not always an easy task for beginners.

Here’s a way around this. When the #4 priority is on a wedge you can just reverse the rules. So now we have two sets of rules:
If the #4 priority is on a dash:
If the #4 priority is on a wedge, reverse the typical rules:

(iii)
Determining R/S When Lowest Priority Group Is In The Plane Of The Page
If the Lowest Priority Group group is in the plane of the page, swapping any two groups will change the configuration from R to S or vice versa. To determine the configuration:
- Swap the #4 substituent with the substituent in the back.
- Redraw the chiral center and determine R/S on the new configuration with the #4 group in the back.
- Flip the result to its opposite to account for the single swap made in step #1.
 When Lowest Priority Group is in the Plane of Page
When Lowest Priority Group is in the Plane of Page
Newman Projection
The Newman projection, which was invented by Newman, is a very straightforward technique for displaying three-dimensional Mathematics on two-dimensional paper.

- The molecule is viewed from the front or along the axis of a carbon-carbon bond in these calculations.
- A point denotes the carbon atom closest to the eye, and a circle denotes the carbon atom farther away. A dot or circle is used to represent the bond between the three atoms or groups on the carbon atoms at 1200 degree angle to one another.
- All parallel bonds are eclipsed and antiparallel or opposite bonds in the Newman projection are staggered.
SawHorse Projection
The sawhorse formula describes how all the atoms or groups are arranged on two nearby carbon atoms. For the sake of clarity, the bonds connecting the two carbon atoms are depicted diagonally and as being substantially longer.

- It is assumed that the carbon in the lower left hand and the upper right hand carbon is the back carbon and the front carbon towards the observer or toward the observer's side, respectively, like ethane.
- In the Sawhorse formula, all parallel bonds are eclipsed while all antiparallel bonds are staggered. Bulky groups are closer to one another at 600 angles in a gauche representation.
Conversion of Fisher Projection in Sawhorse Structure



The above Fisher projection can also be written in Saw Horse form as follows

Conversion of Newmann Projection in to Sawhorse Projection




If all the identical groups are same side or in exactly opposite direction to each other in Newmann projection then compound will be meso.

(Meso) (Meso)
Racemic Mixture & Meso Compounds
There are organic compounds that have similar chemical formulas but different molecular structures. They are called enantiomers. When enantiomers are present in equal quantities in a mixture, it is called a racemic mixture.
- It is an equimolar mixture of R and S or d and l.
- Racemic mixture is optically inactive.
► A compound is optically active due to:
(1) Absence of plane of symmetry (POS)
(2) Absence of centre of symmetry (COS)
 POS
POS
(meso form )
- POS is an imaginary plane where if we place a mirror, mirror image will exactly overlap the other half.
- For meso form, there must be at least two identical chiral carbons.
Identical carbon ⇒ Chiral carbons having identical group attached. - If compound has POS then it will be certainly optically inactive and will be called meso form.
- After finding two identical carbons. We assign them as R or S. If first part is R and other is S then they will rotate the light in opposite direction but to equal extent the compound will be optically inactive. (meso form)

Calculating the Total no. of Optically Active Isomers
1. If a compound have 'n' different chiral carbons then total no. of optically active isomers = 2n
No. of meso form = 0
e.g.

no. of different chiral carbon = 4
total optical isomer = 2n = 24 = 16
- There will be no meso as the compound does not have identical chiral carbon.
- If a compound has n identical chiral centre (symmetrical) ⇒ There must be symmetry from some where.
Example: (Glucose)

Total no. of different chiral carbon = 4
Total Optical Isomers = 24 = 16
(i) If n is even
- number of optical isomers (a) = 2n-1
- meso forms (m) = 2n/2-1
- total number of optical isomers = a + m
(ii) If n is odd

Total optical isomers =  = 2n-1
= 2n-1
Example 1:

- When there is odd no. of identical carbon atom (i.e. symmetrical) then this compound will certainly contain pseudo chiral w.r.t. which compound be symmetrical (i.e. POS).
- Other meso compound of the above compound will form by changing the place Br and H around Pseudo Chiral carbon.

Total meso forms = 2
Total optical isomers = 
= 
= 22 - 2
= 4 - 2 = 2
Here are the two Optical Isomers:

Example 2:

Total no. of even chiral = 4
Number of optical isomers = a =  =
=  = 23 = 8
= 23 = 8
Meso forms = m =  =
=  = 22-1 = 21 = 2
= 22-1 = 21 = 2
Total number of optical isomers = 8 + 2 = 10
Diastereo Isomers through Fischer Projection
For a single chiral centre, there is no diastereoisomer. The stereoisomer which are not related as object and mirror image. They may be optically active or optically inactive.


(Inactive) (active)




► Fix one chiral carbon
After one inter-change
If (R, R) → (R, S)
For compound having 3 chiral carbon to get diastereoisomer, fix two chiral carbon and one interchange with left carbon or fix one chiral carbon and inter change with other two,



(I) (II)
Total isomer = 23 = 8



(III) (IV)
(I) and (III), I and (IV), (II) and (III), (II) and (IV) are diastereoisomers.
Some Solved Examples
Q.1.
(I) 
(II) 
(III) 
(IV) 
What are the relation among the above compounds?
Sol. I and II are identical
III and IV are identical
II and III are diastereo isomer
I and IV are diastereo isomer
Q.2. Find total isomers obtained by dichlorination of cyctopentane?
Sol.

Total isomers = 3 + 3 + 1 = 7
Optically isomers = 6, Optically active isomers = 4
Q.3. Find the total isomers obtained by trichlorination of propane.
Sol.


Total isomers = 6
optically isomers = 2
Q.4. Find total isomers obtained by dichlorination of n-butane
Sol.
 (1)
(1)
 (2)
(2)
 (2)
(2)
 (1)
(1)
 (1)
(1)
 (3) (2 optically 1 meso )
(3) (2 optically 1 meso )
Total isomers = 10 (6 optically active + 1 meso + 3 structural)
Q.5. How many stereoisomers of 1,2,3-cyclohexantriol
Sol.
 No. of Chiral carbon = 3 (identical) symmetrical)
No. of Chiral carbon = 3 (identical) symmetrical)
a =  =
=  = 4- 2
= 4- 2
m = 2
total stereoisomers = 2 + 2 = 4
► 
(Meso)

► Mesoform is optically inactive due to internal compensation and racemic mixture is optically inactive due to external compensation.
Q.6. A and B are enantiomer of each other. Specific rotation of A is 20 º. Rotation of mixture of A and B = -5º what is the percentage of racemic part?
Sol. x mol A, 1-x mol B
x × 20 + ( 1- x ) (-20) = -5
20 x - 20 + 20x = - 5
40 x = 15 ⇒ x = 3/8 = 0.375
moles of A = 3/8
moles of B =  =
= 
 moles of A and
moles of A and  moles of B will form racemic mixture.
moles of B will form racemic mixture.
Enantiomer excess or optical purity =  -
-  =
= 
Q.7.

What is rotation of mixture?
Sol. Rotation will be due to B only,
= 0.3 × (-20º)
= - 6º
► Chiral compound → optically active compound
Q.13. Which of the following compound is Chiral (Optically active)?
(A)

(B)

(C) Both (D) None
Ans. (D)
Allenes, Biphenyls and Spiro Compounds
Allenes, biphenyls, and spiro compounds are interesting classes of organic compounds with unique structural features. Let's explore each of them:
1. Allene system


They are non-superimposable mirror image


(Optically active)

(Inactive)
2. Spiro Compounds


If no. of rings are even ⇒ optically active
If no. of rings are odd ⇒ Inactive

(Optically active)

(Optically Inactive)
 ⇒ This is the even no. of double bonds case.
⇒ This is the even no. of double bonds case.
(Optically active)
► For optical activity, the carbons at extreme position must have different group attached.
► 
⇒ Planar compound
Always have POS, Optically inactive.
3. Biphenyls

If biphenyl contain bulky group at its ortho position (only) then due to repulsion the planarity of compound disappears and its mirror image is non superimposable.
► In the biphenyls none of the two rings must have symmetry.

(Optically inactive)
►  (Optically active)
(Optically active)
In 2º Amines.

Optically inactive due to formation of racemic mixture.
► Order of flipping in amines: 1º > 2º > 3º
D-Form :- For compound having one chiral carbon
(a) If OH is right side → D
(b) If OH is left side → L
(Note: → All the carbon must be in vertical having highest O. N. Carbon on the top)

D-form

L-form
|
127 videos|245 docs|87 tests
|
FAQs on Optical Isomerism - Chemistry Class 11 - NEET
| 1. What is plane polarized light and how is it produced? |  |
| 2. What is the significance of chiral and achiral molecules in optical isomerism? |  |
| 3. How do enantiomers differ from diastereomers? |  |
| 4. How do you assign R-S configuration to chiral centers using wedge-dash notation? |  |
| 5. What are racemic mixtures and meso compounds in the context of optical isomerism? |  |





 (2 Chiral carbon)
(2 Chiral carbon)