Trigonometric Equations | Mathematics (Maths) for JEE Main & Advanced PDF Download
Solution of Trigonometric Equations
A solution of trigonometric equation is the value of the unknown angle that satisfies the equation.
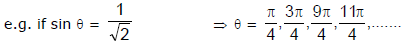
Thus, the trigonometric equation may have infinite number of solutions (because of their periodic nature) and can be classified as :
(1) Principal solution
(2) General solution.
(1) Principal solutions : The solutions of trigonometric equation which lie in the interval [0, 2π) are called principal solutions.
(1) General solutions : The solutions expressing all the values which would satisfy the given equation, and it is expressed in a generalized form in terms of ‘n’.
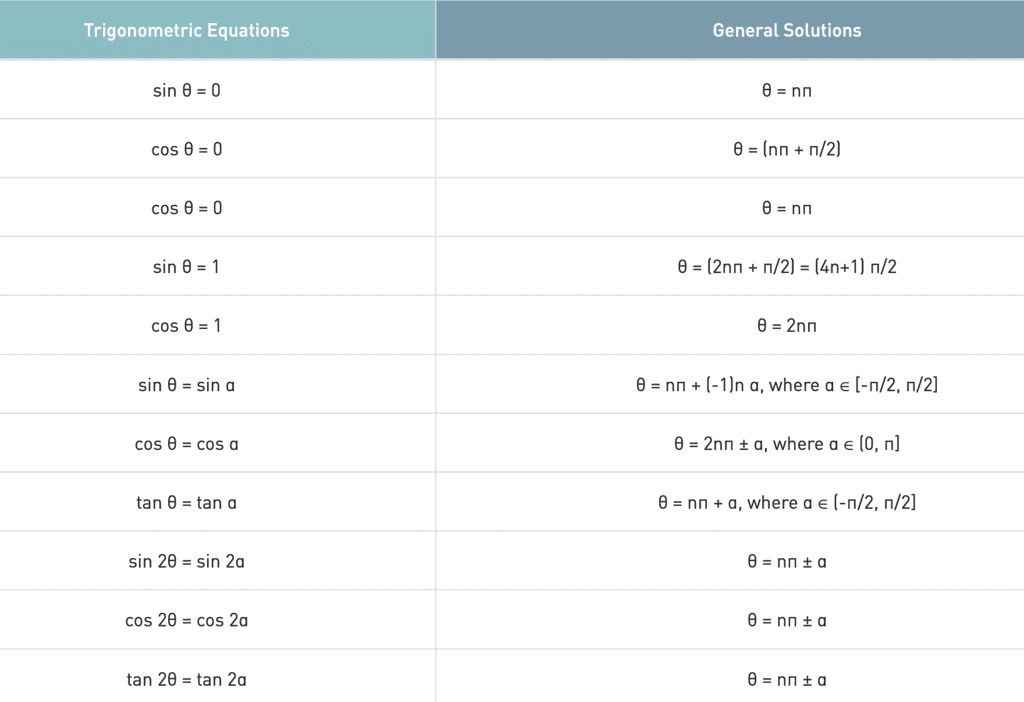 General Solutions of Trigonometric Equations
General Solutions of Trigonometric Equations
Solved Examples:
Ex.1 Find the Principal solutions of the equation sinx = 1/2.
Sol.
sin x = 1/2
there exists two values
i.e. π/6 and 5π/6 which lie in [0,2π) and whose sine is 1/2
Principal solutions of the equation sinx = 1/2 are π/6 and 5π/6
Ex.2 Solve 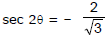
Sol.
Ex.3 Solve tan θ = 2
Sol. tan θ = 2 ....(1)
Let 2 tan α ⇒ tan θ = tan α
⇒ θ= n π + α, where α = tan–1 (2), n ∈ I
Ex.4 Solve 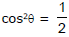
Sol.
Ex.5 Solve 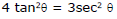
Sol.

Solutions of equations by factorising
Ex.6 Solve the equation sin3 x cos x -sin x cos3x = 1/4.
Sol.
The equation can be written as 4 sin x cos x (sin2 x – cos2 x) = 1,
= –2 sin 2x cos 2x = –sin 4x = 1
Ex.7 Find the general solution of the equation
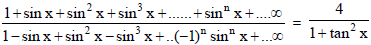
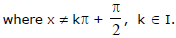
Sol.
Ex.8 Find the general solution of the equation sin3x(1 + cot x) + cos3x(1 + tan x) = cos 2x.
Sol.
sin2x(cos x + sin x) + cos2x (cos x + sin x) = cos 2x
(cos x + sin x)(cos2x + sin2x) = (cos x + sin x)(cos x – sin x)
either cos x + sin x = 0 ....(1) or
cos x - sin x = 1 ....(2)
from (1) tan x = – 1 or 1 – sin 2x = 1 ⇒ sin 2x = 0
If sin 2x = 0 ⇒ 2x = nπ ⇒ x = nπ/2 this is to be rejected because of the tan x or cot x will not be defined so x = (nπ - π/4), n ∈ I
Ex.9Find the solutions of the equation, 
Sol.
2 sin2x = 1 + cos x ; 2 cos2x + cos x – 1 = 0
Solutions of equations reducible to quadratic equations
Ex.10 Solve the equation 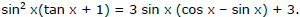
Sol. The given equation makes no sense when cos x = 0; therefore we can suppose that cos x ≠ 0. Noting that the right-hand member of the equation is equal to 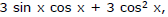 and dividing both members by
and dividing both members by 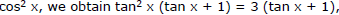
⇒ (tan2 x – 3) (tan x + 1) = 0
⇒
Ex.11 Find the general solution set of the equation logtan x(2 + 4 cos2x) = 2.
Sol.
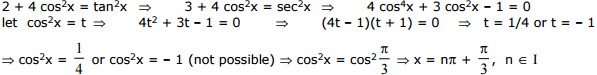
Ex.12 The equation cos2x -sin x + a = 0 has roots when x 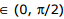 find 'a'.
find 'a'.
Sol. 1 – sin2x – sin x + a = 0 = sin2x + sin x – (a + 1) = 0 (let sin x = t)
t2 + t - (a + 1) = 0,
Ex.13 Solve the equation 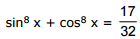
Sol. Using the identity (sin2 x + cos2 x)2 = 1 we get sin4 x + cos4 x = 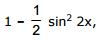
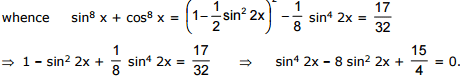
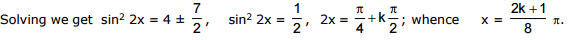
Ex.14 Find all solutions of the equation (tan2 x -1)-1 = 1 + cos 2x, which satisfy the inequality 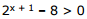
Sol. Let us reduce the initial trigonometric equation to the form 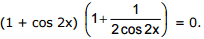
The following values of x are solutions of this equation 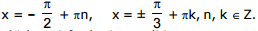
By the hypothesis, we must choose those values of x which satisfy the inequalities
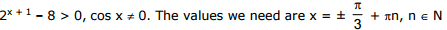
Ex.15 Determine all the values of a for which the equation sin4 x -2 cos2 x + a2 = 0 is solvable. Find the solutions.
Sol. Applying the formula sin4 x = , cos2 x =
and putting cos 2x = t
we rewrite the given equation in the form t2 -6t + 4a2 -3 = 0 ........(1)
The original equation has solutions for a given value of a if and only if, for his value of a, the roots t1 and t2 of the equation (1) are real and at least one of these roots does not exceed unity in its absolute value.
Solving equation (1), we find t1 = 3 -2 , t2 = 3 + 2
.
Hence the rotos of equation (1) are real if 
If condition (2) is fulfilled, then t2 > 1 and, therefore, this root can be dicarded. Thus, the problem is reduced to finding the values of a satisfying condition (2), for which 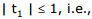

From (3) we find 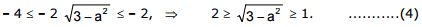
Since the inequality 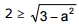 is fulfilled for
is fulfilled for  the system of inequalities (4) is reduced to the inequality
the system of inequalities (4) is reduced to the inequality 
Thus, the original equation is solvable if 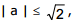 and its solutions are
and its solutions are
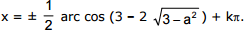
Solving equations by introducing an Auxiliary argument
Ex. 16 Solve sin x + cos x =
Sol. sin x + cos x =
....(i) Here a = 1, b = 1
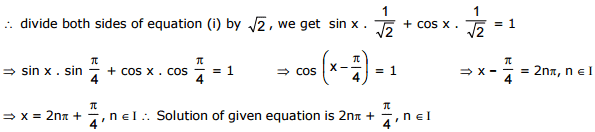
Ex.17 Solve the equation cos 7x -sin 5x = (cos 5x -sin 7x).
Sol.
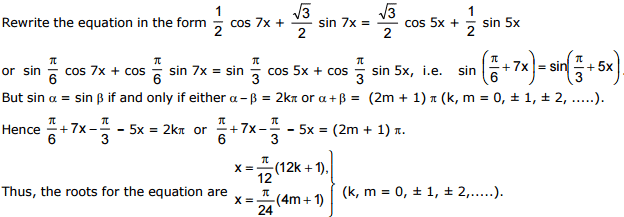
Ex.18 Solve the equation 2 sin 17x + cos 5x + sin 5x = 0
Sol. Dividing both sides of the equation by 2, we reduce it to the form 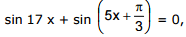
whence we obtain
Ex.19 Solve the equation 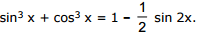
Sol. Using the formula for the sum of cubes of two members we transform the left-hand side of the equation in the following way : 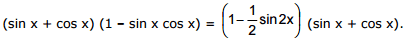
Hence, the original equation takes the form 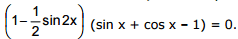
The expression in the first brackets is different from zero for all x. Therefore it is sufficient to consider the equation sin x + cos x -1 = 0. The latter is reduced to the form
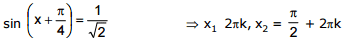
Solving equations by Transforming a sum of Trigonometric functions into a product
Ex.20 Solve cos 3x + sin 2x -sin 4x = 0
Sol.
cos 3x + sin 2x – sin 4 x = 0 ⇒ cos 3x + 2 cos 3x . sin (–x) = 0 ⇒ cos 3x – 2 cos x . sin x = 0
⇒ cos 3x (1 – 2 sin x) = 0 ⇒ cos 3x = 0 or 1 – 2 sin x = 0
solution of given equation is
Solving equations by transforming a product of trigonometric functions into a sum
Ex.21 Solve sin 5x . cos 3x = sin 6x . cos 2x
Sol.
sin 5x . cos 3x = sin 6x . cos 2x
⇒ 2sin 5x . cos 3x = 2sin 6x . cos 2x
⇒ sin 8x + sin 2x = sin 8x + sin 4x
⇒ sin 4x – sin 2x = 0
⇒ 2 sin 2x . cos 2x – sin 2x = 0
⇒ sin 2x (2 cos 2x – 1) = 0
⇒ sin 2x = 0 or 2 cos 2x – 1 = 0 ⇒ 2x = nπ, n ∈ I or cos2x = 1/2
Solving equations by a change of variable
(i) Equations of the form P (sin x ± cos x , sin x . cos x) = 0 , where P (y , z) is a polynomial , can be solved by the change cos x ± sin x = t ⇒ 1 ± 2 sin x . cos x = t2.
(ii) Equations of the form of a . sin x + b . cos x + d = 0 , where a , b & d are real numbers & a, b ≠ 0 can be solved by changing sin x & cos x into their corresponding tangent of half the angle.
(iii) Many equations can be solved by introducing a new variable . eg. the equation sin4 2 x + cos4 2 x = sin 2 x . cos 2 x changes to
Ex.22 
Sol.
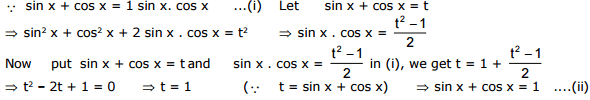
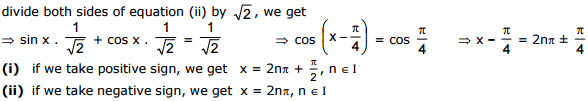
Ex.23 Solve the equation sin 2x -12 (sin x -cos x) + 12 = 0
Sol.
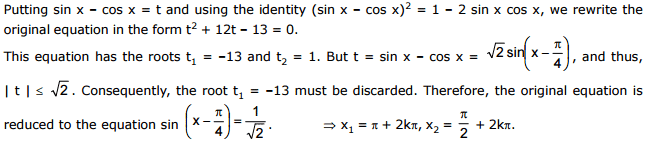
Ex.24 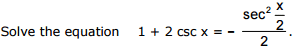
Sol.
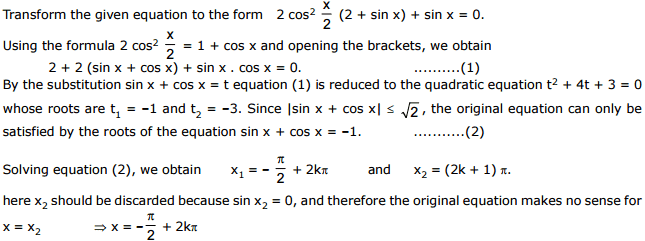
Ex.25 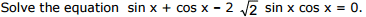
Sol.

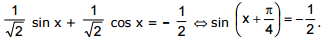
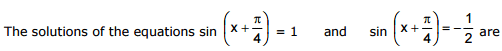

Ex.26 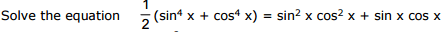
Sol.
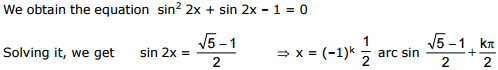
Ex.27 Solve 3 cos x + 4 sin x = 5
Sol.
3 cos x + 4 sin x = 5
equation (i) becomes
Solving equations with the use of the Boundness of the functions sin x & cos x
Ex.28 Solve the equation 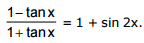
Sol.
The equation makes no sense for x = π/2 + kπ and for x = -π/4 + kπ. For all the other values of x it is equivalent to the equation
After simple transformations we obtain sin x (3 + sin 2x + cos 2x) = 0.
It is obvious that the equation sin 2x + cos 2x + 3 = 0 has no solution, and therefore, the original equation is reduced to the equation sin x = 0 ⇒ x = kπ
Ex.29 Solve the equation (sin x + cos x) √2 = tan x + cot x.
Sol.
Let us transform the equation to the form
....(1)
We have |sin a| ≤ 1, and therefore (1) holds
and
or and
But the first two equations have no roots in common while the second two equations have the common roots x = π/4 + 2k π . Consequently the roots of the given equation are x = π/4 + 2k π
Ex.30 Solve the equation 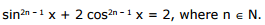
Sol.
Obviously no solution is possible if π/2 < x < 2π as LHS < 2.
If 0 < x < π/2 , then LHS = sin2n – 1 x + 2 cos2n – 1 x < sin2 x + 2 cos2 x = 1 + cos2 x < 2 when n ∈ N – {1}.
Obviously, a solution exists only when x = 0 ⇒ The general solution is x = 2mπ, m ∈ I.
When n = 1
sin x + 2 cos x = 2
Ex.31 Solve the equation 
Sol.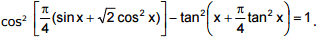
since square of the cosine of any argument doesn't exceed 1, the given equation holds true if and only if we have, simultaneously 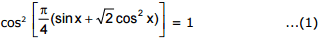

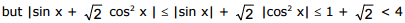
so, equation (3) has no solution for k ≠ 0 for k = 0
sin x + √2 cos2 x = 0 or √2 sin2 x - sinx - √2 or, sinx = -1/√2 , √2
but sin x = √2 is not possible. so only solution to the equation (1) is
equation (2) becomes an identity but
doesn’t satisfy equation (2) so, solution to the original equation
Ex.32 Find the general solution of the equation, sin 3x + cos 4x - 4 sin 7x = cos 10x + sin 17x.
Sol.
(sin 17x - sin 3x) - cos 10x - cos 4x + 4 sin 7x = 0 ⇒ 2 cos 10x sin 7x + 2 sin 7x sin 3x + 4 sin 7x=0
⇒ sin 7x (cos 10x - sin 3x + 2) = 0
Hence sin 7x = 0 ⇒ x = nπ/7, n ∈ I
or cos 10x - sin 3x + 2 = 0 ⇒ cos 10x = - 1 and sin 3x = 1 given x = (4n + 1) π/6
Those starred also satisfy cos 10x = - 1 , the general term of which is
x = 3 (4k - 1) π/6 , k E I , Hence x = nπ/7 or 3(4k + 1) π/6 where, n, k ∈ I
I. Simultaneous equations
Ex.33
Sol. Transform the system to the 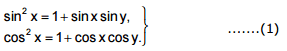
Adding together the equations of system (1) and subtracting the first equation form the second we obtain the system
.....(2)
The first equation of system (2) can be rewritten as 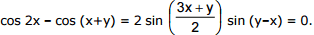
If sin (x – y) = 0, then x – y = kπ. But from the second equation of system (2) we find cos (x – y) = –1, x – y = (2n + 1)π.
Consequently, in this case we have an infinitude of solutions : x – y (2n + 1) π.
then 3x = y = 2kπ. But x – y = (2n + 1) π
Ex.34 Solve the system of equations 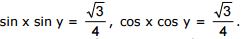
Sol. Adding up the equations of the system, we arrive at an equation
sin x sin y + cos x cos y = √3/2 ⇔ cos (x-y) = √3/2
Subtracting the first equation of the system from the second. we arrive at an equation
cos x cosu y - sin x sin y = √3/2 ⇔ cos (x-y) = 0
Thus the initial system is equivalent to the system
⇔ n, k ∈ Z, cos (x + y) = 0,
Miscellaneous Questions
Ex.35 Solve the equation 2 cot 2x – 3 cot 3x = tan 2x
Sol. The give equation can be rewritten in the form 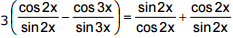
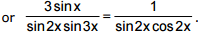
Note that this equation has sense if the condition sin 2x ≠0, sin3x ≠0, cos2x ≠0 holds. For the values of x satisfying this condition we have 3 sin x cos 2x = sin 3x. Transforming the last equation we obtain 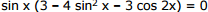 and thus arrive at the equation 2 sin3 x = 0, which is equivalent to the equation sin x = 0. Hence, due to the above note, the original equation has no solutions.
and thus arrive at the equation 2 sin3 x = 0, which is equivalent to the equation sin x = 0. Hence, due to the above note, the original equation has no solutions.
Ex.36 Solve the equation 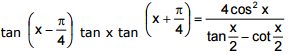
Sol. The right-hand side of the equation is not determined for  , because for
, because for 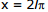 the function
the function 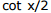 is not defined, for
is not defined, for 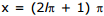 the function tan x/2 is not defined and for
the function tan x/2 is not defined and for
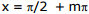 the denominator of the right member of the right member vanishes. For
the denominator of the right member of the right member vanishes. For 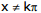 we have
we have.
Hence, for 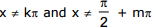 (where k and m are arbitrary integers) the right member of the equation is equal to -2 sin x cos x.
(where k and m are arbitrary integers) the right member of the equation is equal to -2 sin x cos x.
The left member of the equation has no sense for 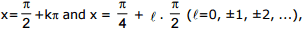 and for all the other values of x it is equal to -tan x because
and for all the other values of x it is equal to -tan x because

Thus, 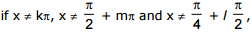 then the original equation is reduced to the form tan x = 2 sin x cos x.
then the original equation is reduced to the form tan x = 2 sin x cos x.
This equation has the roots 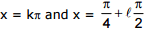 It follows that the original equation has no roots.
It follows that the original equation has no roots.
|
172 videos|503 docs|154 tests
|
FAQs on Trigonometric Equations - Mathematics (Maths) for JEE Main & Advanced
| 1. What are the common methods to solve trigonometric equations? |  |
| 2. How can I solve a trigonometric equation by factorising? |  |
| 3. What does it mean to reduce a trigonometric equation to a quadratic form? |  |
| 4. What is an auxiliary argument in trigonometric equations? |  |
| 5. How can the boundedness of sine and cosine functions help in solving equations? |  |

















