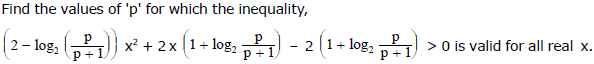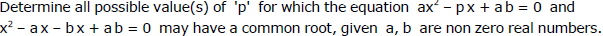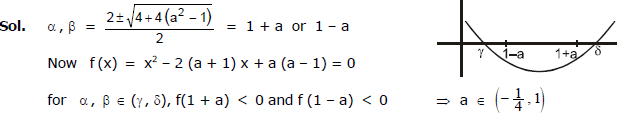Quadratic Equations, Chapter Notes, Class 11, Maths(IIT) PDF Download
QUADRATIC EQUTION
A. General polynomial
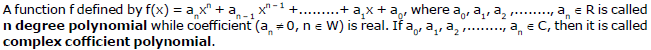
B. Quadratic polynomial
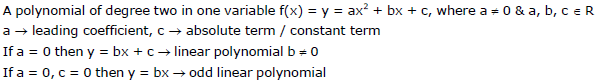
C. Quadratic equation
1. The solution of the quadratic equation , ax� + bx + c = 0 is given by 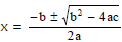
The expression b� - 4 ac = D is called the discriminant of the quadratic equation.
2. If α & β are the roots of the quadratic equation ax� + bx + c = 0 , then ;
(i) αβ = - b/a
(ii) α + β = c/a
(iii) α - β =
D. nature of roots
(1) Consider the quadratic equation ax� + bx + c = 0 where 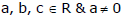 then ;
then ;
(i) D > 0 ⇔ roots are real & distinct (unequal)
(ii) D = 0 ⇔ roots are real & coincident (equal)
(iii) D < 0 ⇔ roots are imaginary
(iv) If p + i q is one root of a quadratic equation, then the other must be the conjugate p - i q & vice versa.
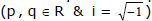
(2) Consider the quadratic equation ax� + bx + c = 0 where 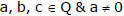 then ;
then ;
(i) If D > 0 & is a perfect square , then roots are rational & unequal .
(ii) If 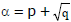 is one root in this case, (where p is rational &
is one root in this case, (where p is rational & is a surd) then the other root must be the conjugate of it
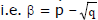 & vice versa.
& vice versa.
E. Graph of Quadratic expression
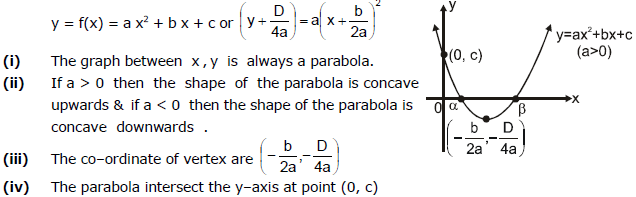
(v) The x-co-ordinate of point of intersection of parabola with x-axis are the real roots of the quadratic equation f(x) = 0. Hence the parabola may or may not intersect the x-axis at real points.
Consider the quadratic expression , y = ax� + bx + c , a ≠ 0 & a , b , c ∈ R then ;
(i) " x ∈ R , y > 0 only if a > 0 & b� – 4ac < 0 (figure 3).
(ii) " x ∈ R , y < 0 only if a < 0 & b� – 4ac < 0 (figure 6).
=========================================================================
F. relation between roots & coefficients

Ex.1 A quadratic polynomial p(x) has 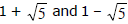 as roots and it satisfies p(1) = 2. Find the quadratic polynomial.
as roots and it satisfies p(1) = 2. Find the quadratic polynomial.
Sol. sum of the roots = 2, product of the roots = - 4
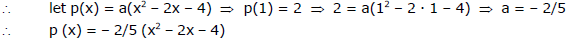
Ex.2 The quadratic equation x2 + mx + n = 0 has roots which are twice those of x2 + px + m = 0 and m, n and p 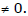 Find the value of
Find the value of .
Sol.
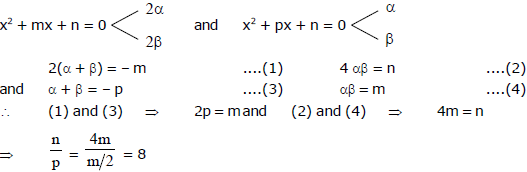
Ex.3 Find the range of the variable x satisfying the quadratic equation,
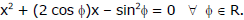
Sol.
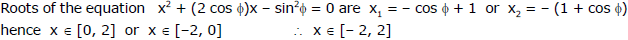
Ex.4
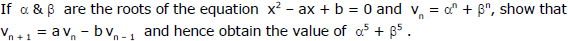
Sol. 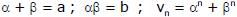

Ex.5 One root of mx2 - 10x + 3 = 0 is two third of the other root. Find the sum of the roots.
Sol.
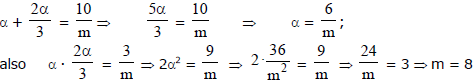
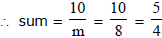
Ex.6 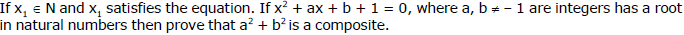
Sol.
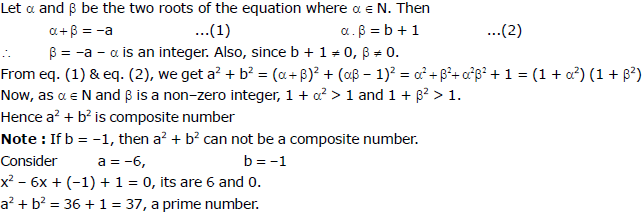
Ex.7 Find a quadratic equation whose roots x1and x2 satisfy the condition
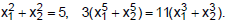 (Assume that x1, x2 are real)
(Assume that x1, x2 are real)
Sol.
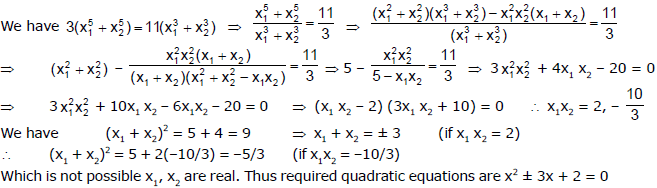
Ex.8 Form a quadratic equation with rational coefficients if one of its root is cot218�.
Sol.
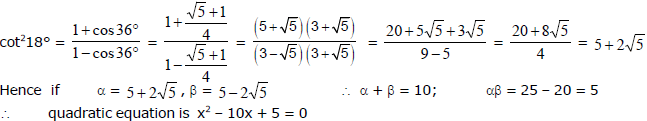
Ex.9 Let a & c be prime numbers and b an integer. Given that the quadratic equation a x2 + b x + c = 0 has rational roots, show that one of the root is independent of the co-efficients. Find the two roots.
Sol.
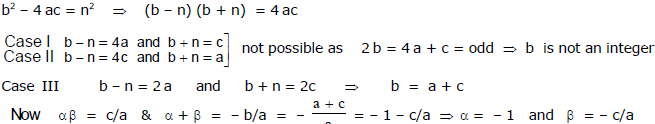
Ex.10 Find all integers values of a such that the quadratic expressions (x + a) (x + 1991) + 1 can be factored as (x + b) (x + c), where b and c are integers.
Sol.
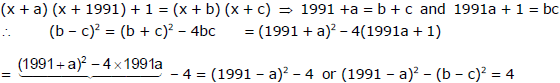
If the difference between two perfect square is 4, then one of them is 4 and the other is zero.
Therefore, 1991 - a = � 2, (b - c)2 = 0
⇒ a = 1991 + 2 = 1993 and b = c or a = 1991 - 2 = 1989 and b = c
But b + c = 2b = 1991 + a = 1991 + 1993 or 1991 + 1989 ⇒ b = c = 1992 or 1990
So, the only 2 values of a are 1993 and 1989.
Ex.11 Find a, if ax2 - 4x + 9 = 0 has integral roots.
Sol. 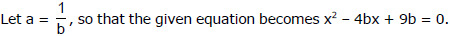
This equation has integeral roots if b is an integer and 16b2 - 36b is a perfect square
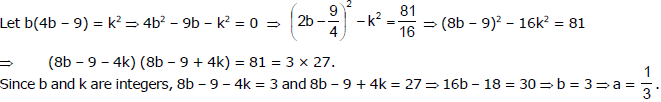
For any other factorization of 81, b will not be an integer.
Ex.12 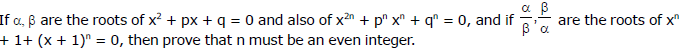
Sol.
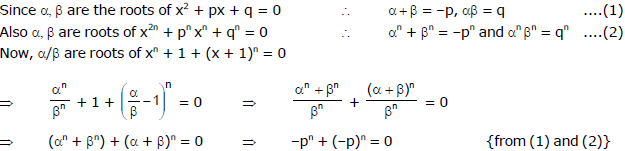
This is true only if n is an even integer.
Ex.13 Find all values of the parameter a for which the quadratic equation (a+1) x2 + 2(a + 1) x + a - 2 = 0
(a) has two distinct roots,
(b) has no roots,
(c) has two equal roots.
Sol. By the hypothesis this equation is quadratic, and therefore 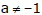 and the discriminant of this equation
and the discriminant of this equation 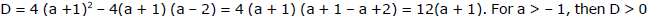 then this equation has two distinct roots. For
then this equation has two distinct roots. For 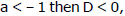 then this equation has no roots. This equation can not have two equal roots since D = 0 only for a = -1, and this contradicts the hypothesis.
then this equation has no roots. This equation can not have two equal roots since D = 0 only for a = -1, and this contradicts the hypothesis.
Ex.14 If the equation ax2 + 2bx + c = 0 has real roots, a, b, c being real numbers and if m and n are real numbers such that m2 > n > 0 then prove that the equation ax2 + 2mbx + nc = 0 has real roots.
Sol.
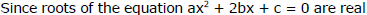
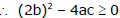
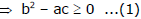
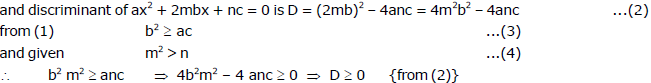
Hence roots of equation ax2 + 2mbx + nc = 0 are real.
Ex.15 Show that the expression x2 + 2(a + b + c) x + 3(bc + ca + ab) will be a perfect square if a = b = c.
Sol. Given quadratic expression will be a perfect square if the discriminant of its corresponding equation is zero.

Ex.16 If c < 0 and ax2 + bx + c = 0 does not have any real roots then prove that
(i) a - b + c < 0
(ii) 9a + 3b + c < 0.
Sol.
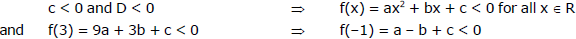
=========================================================================
G. Equation v/s Identity
A quadratic equation is satisfied by exactly two values of `x' which may be real or imaginary. The equation, a x2 + b x + c = 0 is :
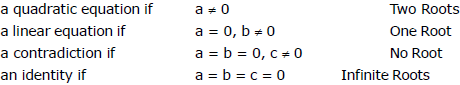
If a quadratic equation is satisfied by three distinct values of `x', then it is an identity.
(x + 1)2 = x2 + 2x + 1 is an identity in x.
Here highest power of x in the given relation is 2 and this relation is satisfied by three different values x = 0, x = 1 and x = -1 and hence it is an identity because a polynomial equation of nth degree cannot have more than n distinct roots.
Ex.17 If 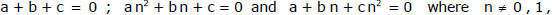 then prove that a = b = c = 0 .
then prove that a = b = c = 0 .
Sol.
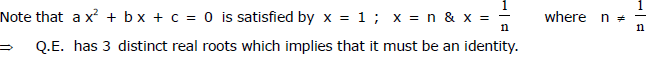
Ex.18
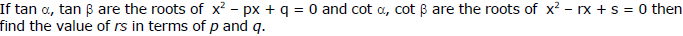
Sol. 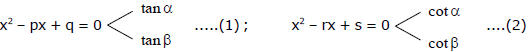
hence roots of 2nd are reciprocal of (1)
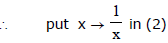
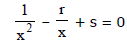
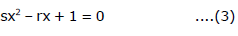
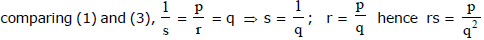
H. Solution of Quadratic Inequalities
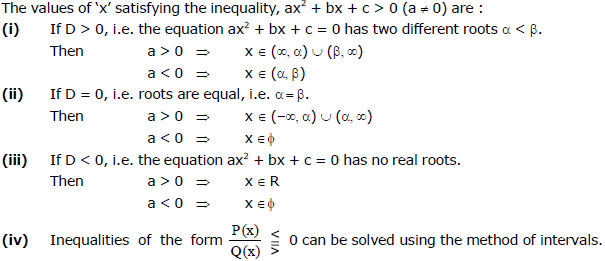
Ex.19 Find the solution set of k so that y = kx is secant to the curve y = x2 + k.
Sol.
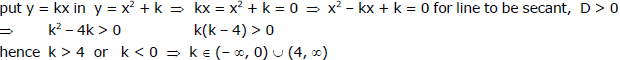
Ex.20
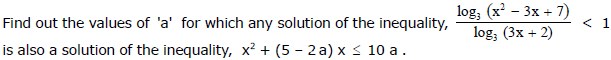
Sol.
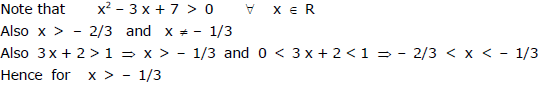
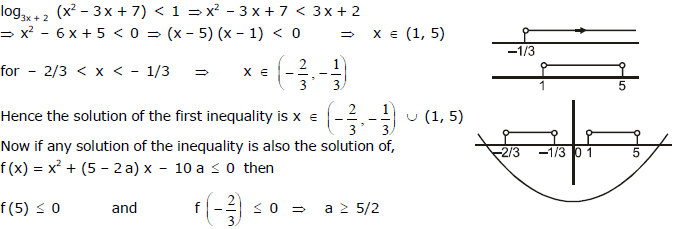
Ex. 21
Sol.
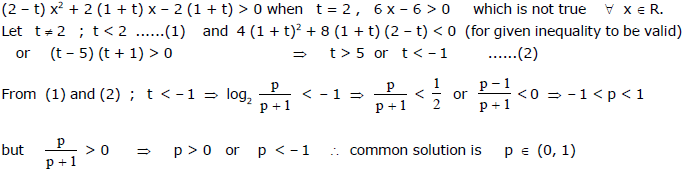
=========================================================================
I. Range of Quadratic Expression f(x) = ax2 + bx + c
(i) Range when x ε R :
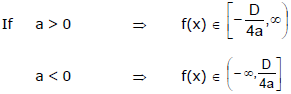
Maximum & Minimum Value of y = ax� + bx + c occurs at x = - (b/2a) according as a < 0 or a > 0 respectively
(ii)
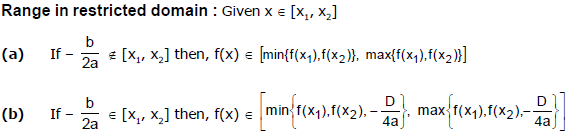
Ex.22 Find the minimum value of f(x) = x2 - 5x + 6.
Sol.
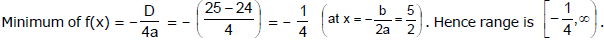
Ex.23 Let P(x) = ax2 + bx + 8 is a quadratic polynomial. If the minimum value of P(x) is 6 when x = 2, find the values of a and b.
Sol.
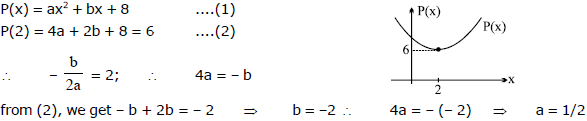
Ex.24
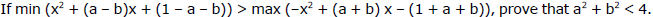
Sol.
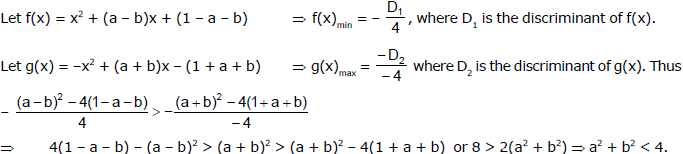
Ex.25 The coefficient of the quadratic equation ax2 + (a + d)x + (a + 2d) = 0 are consecutive terms of a positively valued, increasing arithmetic sequence. Determine the least integral value of d/a such that the equation has real solutions.
Sol.
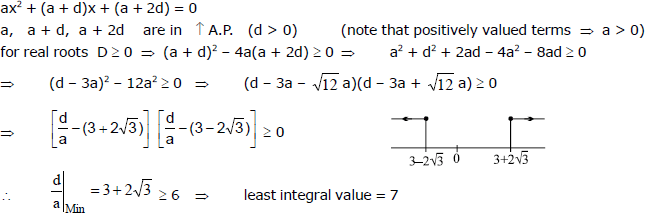
Ex.26
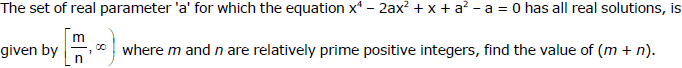
Sol.
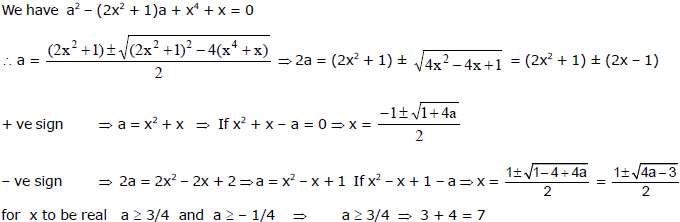
Ex.27 
Sol.
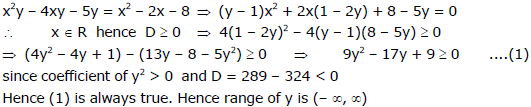
=========================================================================
J. Resolution of a Second Degree Expression in X and Y
The condition that a quadratic function f (x , y) = ax� + 2 hxy + by� + 2 gx + 2 fy + c may be resolved into two 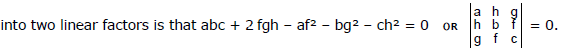
Ex.28 If x is real and 4y2 + 4xy + x + 6 = 0, then find the complete set of values of x for which y is real.
Sol.
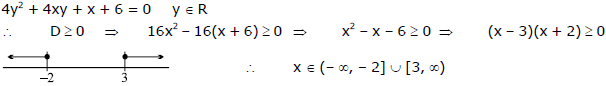
Ex.29 Find the greatest and the least real values of x & y satisfying the relation, x2 + y2 = 6 x - 8 y.
Sol. writing as a quadratic in y , y2 + 8 y + x2 - 6 x = 0
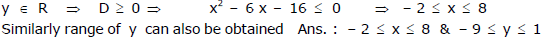
Ex.30 If x, y ans z are three real numbers such that x+y+z = 4 and x2+ y2+z2 = 6, then show that each
Sol.
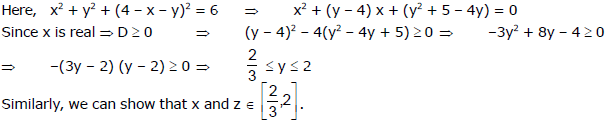
K. Theory of Equations

Note :

Ex.31 If x = 1 and x = 2 are solutions of the equation x3 + ax2 + bx + c = 0 and a + b = 1, then find the value of b.
Sol.
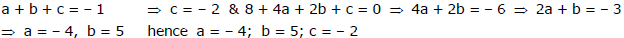
Ex.32 A polynomial in x of degree greater than 3 leaves the remainder 2, 1 and - 1 when divided by
(x - 1); (x + 2) & (x + 1) respectively . Find the remainder, if the polynomial is divided by,
(x2 - 1) (x + 2) .
Sol.
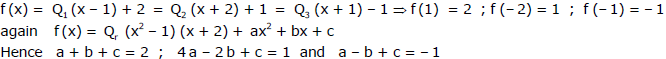
Ex.33 Find the roots of the equation x4 + x3 - 19x2 - 49x - 30, given that the roots are all rational numbers.
Sol. Since all the roots are rational because, they are the divisors of -30.
The divisors of -30 are � 1, � 2, � 3, � 5, � 6, � 10, � 15, � 30.
By remainder theorem, we find that -1, -2, - 3, and 5 are the roots.
Hence the roots are -1, -2, -3 and + 5.
Ex.34 From the equation of the lowest degree with rational co-efficients, which has 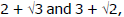 as two of its roots.
as two of its roots.
Sol.
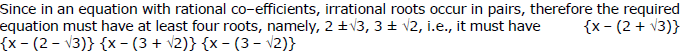 as a factor, i.e., it must have {(x - 2)2 - 3} {(x - 3)2 -2)} ...(1)
as a factor, i.e., it must have {(x - 2)2 - 3} {(x - 3)2 -2)} ...(1)
Since the co-efficients of (1) are rational, therefore {(x - 2)2 - 3} {(x - 3)2 - 2} = 0 is required equation.
Ex.35 Let u, v be two real numbers such that u, v and uv are roots of a cubic polynomial with rational coefficients. Prove or disprove uv is rational.
Sol. Let x3 + ax2 + bx + c = 0 be the cubic polynomial of which u, v and uv are the roots and a, b, c are all rationals.
u + v + uv = -a ⇒ u + v = -a - uv, uv + uv2 + u2 v = b and u2v2 = - c
⇒ b = uv + uv2 + u2v = uv (1 + v + u) = uv (1 - a - uv) = (1 - a) uv - u2v2 = (1 - a) uv + c
i.e., uv = and since a, b, c are rational, uv is rational.
Ex.36
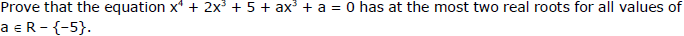
Sol. The given expression is (x3 + 1)2 + a (x3 + 1) + 4 = 0
If discriminant of the above equation is less than zero i.e. D < 0
Then we have six complex roots and no real roots.

we will get two real roots and other roots will be complex except when t = 1 is one of the roots
⇒ f(1) = 0 ⇒ a = -5.
Ex.37
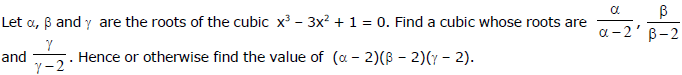
Sol.
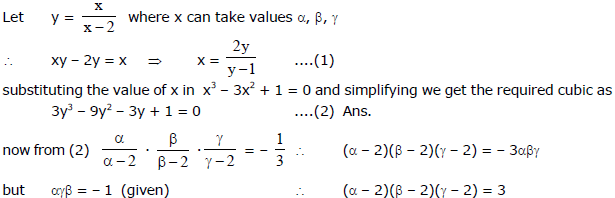
Ex.38 If p(x) is a polynomial with integer coefficients and a, b, c are three distinct integers, then show that it is impossible to have p(a) = b, p(b) = c and p(c) = a.
Sol. Suppose a, b, c are distinct integers such that p(a) = b, p(b) = c and p(c) = a. Then
p(a) - p(b) = b - c, p(b) - p(c) = c - a, p(c) - p(a) = a - b.
But for any two integers m � n, m - n divides p(m) - p(n). Thus we get,
a - b | b - c, b - c | c - a, c - a|a - b.
Therefore a = b = c, a contradiction, Hence there are no integers a, b, and c such that p(a) = b, p(b) = c and p(c) = a.
Ex.39 Find all cubic polynomials p(x) such that (x - 1)2 is a factor of p(x) + 2 and (x + 1)2 is a factor of p(x) - 2.
Sol.
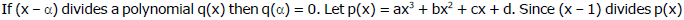
+ 2, we get a + b + c + d + 2 = 0.
Hence d = -a - b - c - 2 and
p(x) + 2 = a(x3 - 1) + b(x2 - 1) + c(x - 1) = (x - 1) {a(x2 + x +1) + b(x + 1) + c}.
Since (x - 1)2 divides p(x) + 2, we conclude that (x - 1) divides a(x2 + x + 1) + b(x + 1) c. This implies that 3a + 2b + c = 0. Similarly, using the information that (x + 1)2 divides p(x) - 2, we get two more relations : -a + b - c + d - 2 = 0; 3a - 2b + c = 0. Solving these for a, b, c, d, we obtain b = d = 0, and a = 1, c = -3. Thus there is only one polynomial satisfying the given condition : p(x) = x3 - 3x.
=========================================================================
L. Common Roots of Quadratic Equations
Atleast one Common Root :
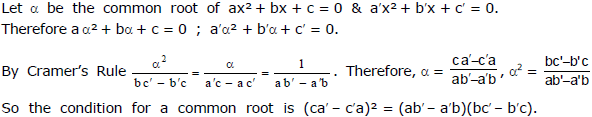
Note : If f(x) = 0 & g(x) = 0 are two polynomial equation having some common roots(s) then those common root(s) is/are also the root(s) of h(x) = a f(x) + bg (x) = 0.
Ex.40
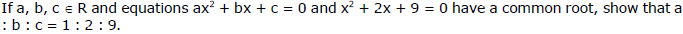
Sol. Given equations are : x2 + 2x + 9 = 0 .... (i) and ax2 + bx + c = 0 .... (ii)
Clearly roots of equation (i) are imgainary since equation (i) and (ii) have a common root, therefore common root must be imaginary and hence both roots will be common.

Ex.41 Determine a such that x2 - 11x + a and x2 - 14x + 2a may have a common factor.
Sol.
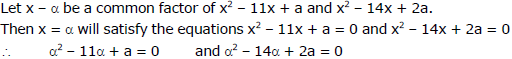
Solving (i) and (ii) by cross multiplication method, we get a = 24.
Ex.42 If the quadratic equations, x2 + bx + c = 0 and bx2 + cx + 1 = 0 have a common root then prove that either b + c + 1 = 0 or b2 + c2 + 1 = b c + b + c .
Sol.
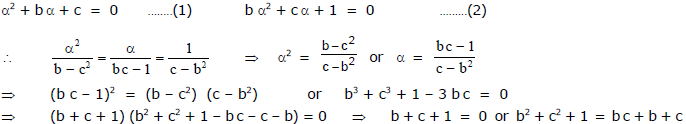
Ex.43
Sol. x2 - (a + b) x + a b = 0 or (x - a) (x - b) = 0 ⇒ x = a or b
Ex.44 If x2 - ax + b = 0 and x2 - px + q = 0 have a root in common and the second equation has equal roots show that b + q = .
Sol. Given equation are x2 - ax + b = 0 ans x2 - px + q = 0. Let a be the common root. Then roots of equation (2) will be a and a. Let b be the other root of equation (1). Thus roots of equation (1) are a, b and those of equation (2) are α, α.
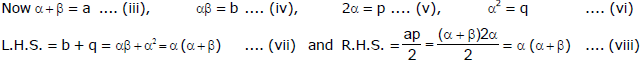
from (7) and (8), L.H.S. = R.H.S.
Ex.45 If each pair of the following three equations x2 + ax + b = 0, x2 + cx + d = 0, x2 + ex + f = 0 has exactly one root in common, then show that (a + c + e)2 = 4 (ac + ce + ea - b - d - f)
Sol. x2 +ax + b = 0 ...(1)
x2 + cx + d = 0 ...(2)
x2 + ex + f = 0 ...(3)
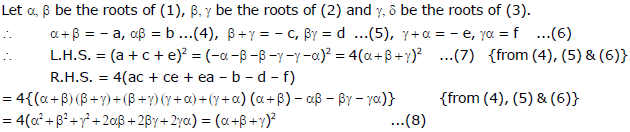
From (7) & (8), (a + c + e)2 = 4 (ac + ce + ea - b - d - f)
Ex.46
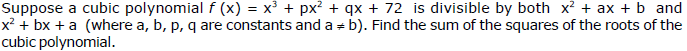
Sol. Since cubic is divisible by both x2 + ax + b and x2 + bx + a and
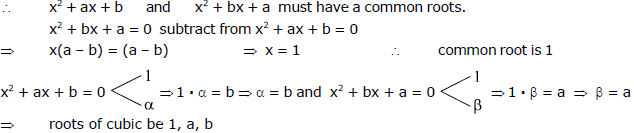
product of the roots be 1 � a � b = - 72 ...(1) and a + b + 1 = 0 ...(2) (from x2 + ax + b = 0 put x = 1)
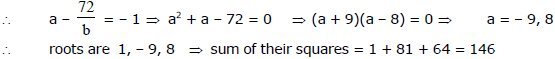
=========================================================================
M. Location of Roots
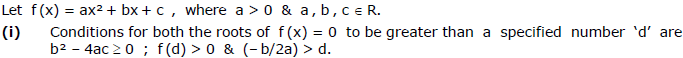
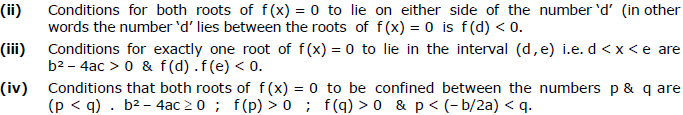
Ex.47
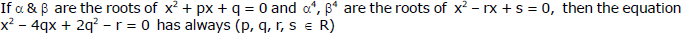
Sol.
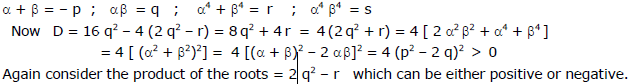
Ex.48 Find the set of values of 'p' for which the quadratic equation, (p - 5) x2 - 2 px - 4 p = 0 has atleast one positive root.
Sol.
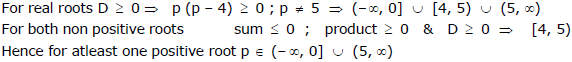
Ex.49
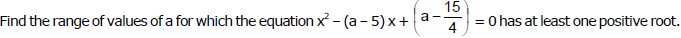
Sol.
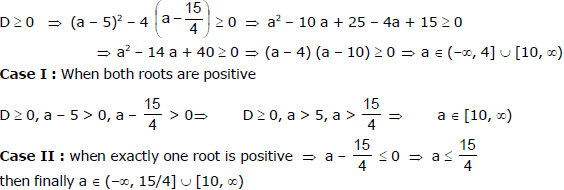
Ex.50 Find all the values of `a' for which both the roots of the equation.
(a - 2)x2 + 2ax + (a + 3) = 0 lies in the interval (-2, 1).
Sol.
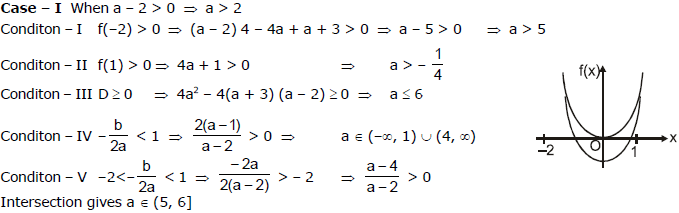
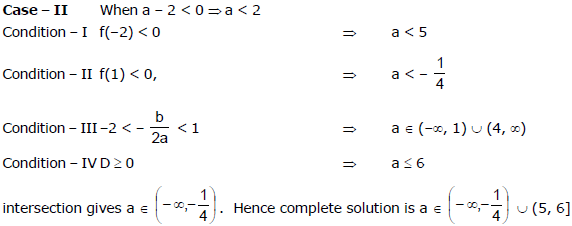
Ex.51 The coefficients of the equation ax2 + bx + c = 0 where 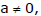 satisfy the inequality
satisfy the inequality
(a + b + c)(4a - 2b + c) < 0. Prove that this equation has 2 distinct real solutions.
Sol.
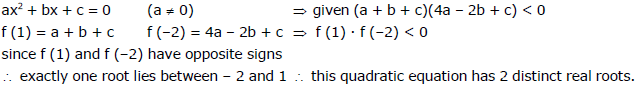
Ex.52 Find the value of k for which one root of the equation of x2 - (k + 1)x + k2 + k-8=0 exceed 2 and other is smaller than 2.
Sol.
Ex.53
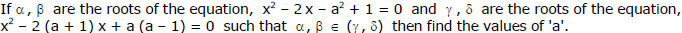
Ex.54 (a) For what values of `a' exactly one root of the equation 2ax2 - 4ax + 2a - 1 = 0, lies between a and 2.
(b) Find all values of a for which the equation 2x2 - 2(2a + 1) x + a(a + 1) = 0 has two roots, one of which is greater than a and the other is smaller than a.
Sol.
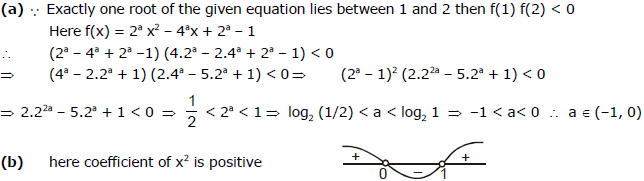
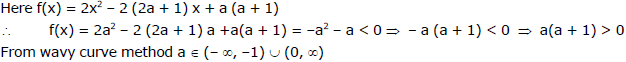
Ex.55 Find all values of k for which the inequality, 2 x2 - 4 k2 x - k2 + 1 > 0 is valid for all real x which do not exceed unity in the absolute value .
Sol.
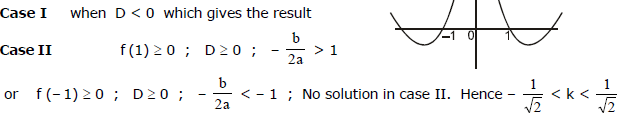
FAQs on Quadratic Equations, Chapter Notes, Class 11, Maths(IIT)
| 1. What are quadratic equations? |  |
| 2. What is the quadratic formula? |  |
| 3. How do you solve quadratic equations by factoring? |  |
| 4. What is the discriminant of a quadratic equation? |  |
| 5. What are the applications of quadratic equations? |  |